JTE - Fall 2007 v19n1 - Engineering Modeling Using a Design Paradigm: A Graphical Programming-Based Example
Engineering Modeling Using a Design Paradigm: A Graphical Programming-Based Example
Paul D. Schreuders
Introduction
Engineers combine design paradigms or methods for problem solving ( “OED Online”, 2004 ) with mathematical modeling techniques to predict the success of their designs, a method that they have found to be accurate and repeatable. However, computer models are not just used in traditional engineering design and practice. Many computer games have complex mathematical models hidden behind their interfaces. Beyond the obvious examples, such as the Sims™ and SimCity™, the “first person shooters” contain extensive physics models, so that thrown objects and jumping characters behave correctly on the screen ( “Best of What's New 2005”, 2005 ; Tamaki, 2006 ; Terzopoulos, 1999 ).
As engineering has moved into the biological arena, engineering modeling has been used to describe living processes through the creation of constructs that reproduce, move, and eat. The reverse is also true. Modeling has adopted into its array of methods for solving problems, biological approaches such as neural networks and evolution-based optimization ( Kim & Cho, 2006 ; Terzopoulos, 1999 ).
Mathematical models are also becoming increasingly important in the workplace. Businesses use models to optimize their future plans. Brokers use models to identify when to buy and sell stocks. Actuaries use models to predict death rates for insurance companies. Biologists use models to predict the impact of changes to the environment ( Gotelli, 1998 ; Kurzweil, 1999 ).The teaching of model development is primed to move into the high school classroom for several reasons. These reasons include the removal of barriers to modeling, the inclusion of modeling in national curricular standards, and the adoption of pre-engineering curricula by many high schools.
First, many of the barriers to teaching modeling have been removed. As the computer gaming industry has demonstrated, the hardware for modeling is both available and affordable. Further, analyses such as Moore’s Law indicate that computer hardware will become exponentially faster for the reasonable future ( Kurzweil, 1999 ). The software required to create these models has also matured and become easier to use.
Second, modeling integrates technology education, science education, and mathematics education by linking the design standards from the Standards for Technological Literacy ( ITEA & TAAP, 2000 ) and the National Science Education Standards ( National Research Council [U.S.], 1996 ) with the mathematical modeling standards of the Principles and Standards for School Mathematics ( National Council of Teachers of Mathematics, 1989 ).
Finally, there is a continuing trend towards the adoption of engineering design into the high school curriculum. Project Lead the Way, for example, has over 1300 participating schools in 45 states ( PLTW, 2006 ). This trend is evident with the development of the Standards for Technological Literacy: Content for the Study of Technology (STL) and its endorsement by William A. Wulf, former President of the National Academy of Engineering ( ITEA & TAAP, 2000 ). Engineering design emphasizes analysis and modeling. The development of student appropriate methods for engineering analysis represents some of the biggest remaining challenges in bringing engineering design into the high school. As shown in Table 1, there are a number of ways that analysis has been approached.
| Methodology | Limitation |
|---|---|
| Student computation | Restricted by the students’ mathematical background; often limits the problems to those soluble by algebra or trigonometry |
| Use of tabular or graphical data | Student solutions are limited to those considered in advance of the project |
| Use of software (pre-programmed) | Student solutions are limited to those considered in advance of the project |
| Student written software | Requires extensive class time to teach programming/write the software; restricted by the students’ mathematical background |
| Experimental/trial-and error | Inefficient in creating designs; students often fail to understand the science and technologies behind their design; time consuming |
| Graphical modeling | Requires modeling software; Unfamiliar to most technology teachers |
There is a tendency to consider engineering design paradigms as primarily applicable to the creation of physical objects or, perhaps, software. A more appropriate view, however, is to view the design process as a paradigm for problem solving with the goal of creation. Historically, this paradigm has been amazingly effective for the creation and implementation of new ideas and inventions. It is used for the identification of the boundaries of possible designs and for the elimination of impossible, impractical, inefficient, or otherwise undesirable designs. A number of design paradigms have been developed for use in the classroom ( Eggert, 2004 ; Gomez, Oakes, & Leone, 2004 ; Haik, 2003 ; Oakes, Leone, & Gunn, 2004 ). In general, these paradigms differ only in minor ways. One of these paradigms is shown in Table 2. The design process includes a series of tradeoffs that alter what is considered the optimal product. There may, in fact, be multiple optimal designs ( Koen, 2003 ). The adoption of the design paradigm for model development has an advantage in that it is a process with which technology educators and their students are familiar and proficient in using, allowing the transfer of existing skills. It provides a useful, structured approach to introducing engineering analysis into the classroom, a goal and a challenge for many pre-engineering programs.
|
Stage
Number |
Design Paradigm
( Gomez, Oakes, & Leone, 2004 ; Oakes, Leone, & Gunn, 2004 ) |
Modeling Paradigm |
|---|---|---|
| Stage 1: | Identify the problem/product innovation | Identify the system to be analyzed or simulated |
| Stage 2: | Define the working criteria/goals | Identify the information to be obtained from the model |
| Stage 3: | Research and gather data | Research and gather data |
| Stage 4: | Brainstorm/generate creative ideas | Brainstorm/generate model structures |
| Stage 5: | Analyze potential solutions | Develop and refine model structures |
| Stage 6: | Develop and test models | Implement the model |
| Stage 7: | Make the decision | Specify and simulate |
| Stage 8: | Communicate and specify | Interpret and communicate |
| Stage 9: | Implement and commercialize | Protect and commercialize |
| Stage 10: | Perform post-implementation review | Perform post-implementation review |
Until recently, modeling required significant programming expertise and/or the knowledge of differential equations in order to analyze dynamic systems ( Coughanowr & Koppel, 1965 ; Lewis & Yang, 1997 ; Ogata, 1997 ). However, with the maturation of graphical modeling software, this is no longer true. In this article, a design-based approach to engineering model development will be examined. Graphical approaches emphasize the development of a model’s structure prior to its implementation.
Graphical Modeling Software
In graphical modeling software, programming is performed by manipulating graphical elements and their connections. Educators familiar with using RoboPRO ( “ROBO Pro”, 2005 ) or Robolab ( “Robolab”, 2004 ) to control robots will find that the techniques used in graphical modeling software are quite similar. In addition, because of their emphasis on model structure and minimal programming requirements, graphical modeling software allows the development and solution of complex mathematical models rapidly with limited mathematical background.
A number of engineering-specific graphical modeling software packages exist. However, because they presume significant discipline-specific expertise and are expensive, these packages are not useful in the high school classroom. Fortunately, a number of generalized modeling packages exist, including Simulink ( “Simulink”, 2005 ), Berkeley Madonna ( Zahnley, 2006 ), and Stella ( “Stella”, 2005 ). Simulink is the most powerful of these packages, but the least friendly to the student user. Stella is the least powerful package, but is by far the most student friendly. Madonna lies somewhere in between the other two. All three packages are available with academic discounts at prices ranging from $50 for a single copy to a site license for around $1000.
Mathematical models of dynamic systems contain variables known as “state variables.” These variables and their inflows and outflows are described by sets of first order differential equations ( Ogata, 1997 ; Phillips & Harbor, 1996 ). The solution to the model is obtained by simultaneously solving these differential equations. The flows are described using flow rate coefficients, equations, etc. ( Hannon & Ruth, 1997 ; Richmond, 2004 ). In graphical programming software, all of the above information is entered using a graphical interface. Then, hidden to the user, the software solves the differential equations, using one of several numerical integration methods.
In practice, the link between a graphical description of a system and the graphical program of the systems is clearest for classes of problems where each state variable represents a reservoir of things and the things flow between those reservoirs along defined pathways. Some examples of this type of systems include movement of liquid between tanks, storage, movement and distribution of energy in an automobile, and movement of money through a business. Techniques for converting equations directly into graphical programs are available ( Ogata, 1997 ). However, the resulting graphical programs often bear little resemblance to diagrams of the physical system, making them more challenging to use in the classroom.
The clearest way to show the benefits of graphical model development is using an example. This article will model the spread of a computer virus through a school’s computer laboratories. The most obvious benefit of such a model is as an aid to developing strategies for combating computer virus infection, reducing the cost to companies and individuals. Models of a computer virus infection can also examine a computer network’s vulnerability to disruption and suggest possible areas for improvement.
Stella software will be used herein to create the model. However, any of the generalized graphical modeling software packages could be used. Educators will find that Stella requires a minimal amount of instruction (typically on the order of a few hours) for students to develop basic facility in its use. In addition, a wide range of problems have been solved using this software, so that grade appropriate problems are available in both the scientific literature and in books ( Fisher, 2005a , 2005b ; Hannon & Ruth, 1994 , 1997 ; Richmond, 2004 ).
The Virus Model’s Development Process
This paper will develop and demonstrate an approach to modeling using a ten-stage modeling protocol, adapted from engineering design protocols ( Gomez, Oakes, & Leone, 2004 ; Oakes, Leone, & Gunn, 2004 ), to model the spread of a computer virus. The design model paradigm is shown in Figure 1.
Stage 1. Identify the system to be analyzed or simulated
In system identification, the model’s contents are chosen and extraneous content is eliminated from the model. It has several aspects. The first is identification of what system is to be modeled and what components of that system are to be included in the model. As part of this, the nature of the system needs to be analyzed. An important component of this analysis is the isolation of the root process to be modeled. In this example, the behavior of the virus is the root process. The brand of operating system is relevant only if it alters the system’s behavior. The next important aspect of system identification is the definition of the system’s scope and resolution, i.e., what will not be modeled. For example, in this example, the Internet will not be considered. In addition, the network speed will not be considered, since it operates at speeds that are orders of magnitude faster than the processes being modeled.
Identification of the system for this example must consider the three main categories of computer viruses: file infector viruses, boot-sector viruses, and macro viruses ( Kephart, Sorkin, Chess, & White, 1997 ). The greater majority of known viruses belong to the first category, infecting application files such as games, spread-sheets, and word processors. The second category, boot-sector viruses, reside with the start-up information executed when a computer first starts up. Once in place, a boot-sector virus can infect any electronic storage media used on that computer. Many computer applications today allow the program to run macros or scripts, which are small sub-programs used to perform
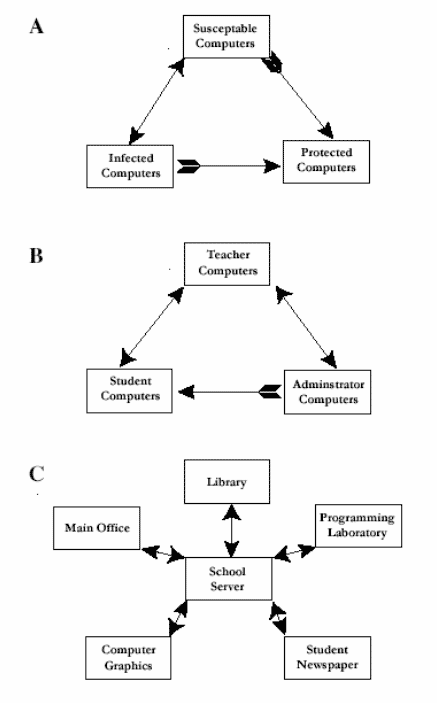
Figure 1. A graphical depiction of some possible approaches for grouping computers in a computer virus model. The computers have been grouped by virus infection status (A), user type (B), and location (C).
repeated actions or a series of actions quickly. The final category of viruses, macro viruses, infect the data files that are freely and rapidly shared by users. A data file infected with a macro virus will execute a viral macro script in response to the actions of the user. These are the most prevalent of all viruses ( Kephart, Sorkin, Chess, & White, 1997 ) and are the type of virus that we wish to model.
Stage 2. Identify the information to be obtained from the model
Once an overall understanding of the system has been developed, the question that motivates the model needs to be formulated. The formulation of this question is critically important, since it provides the foundation for designing the model. Asking the question: “How fast will our school become infected when a new macro computer virus appears?” will yield a vastly different model than “Will my computer become infected by the new virus?” In the first question, the model examines the average behavior of the computers, whereas for the second question the model examines the behavior of individual computers. Like most design processes, modeling is a balancing act. Improving the quality of a model (e.g., increasing accuracy or adding functionality) must be balanced against cost (e.g., time or money). Formulating the question appropriately provides the basis for the balancing decisions. In demonstrating this approach to model development, we will answer the first question.
Stage 3. Research and gather data
Most new models are based on existing knowledge/models and modified and refined to fit the problem at hand. In this stage of model development, the modeler develops an understanding of the process of interest and of the existing models. The viruses under consideration have three main aspects, the payload, the dormancy period, and the infection component ( Thimbleby, Anderson, & Cairns, 1999 ). The payload is the set of commands that, when executed, do something undesirable. The dormancy period is the time lapse between infection and manifestation, where the infection may lay hidden or concealed before manifesting itself. This delay makes the program more difficult to detect by distancing the payload’s actions from the time of infection. The third aspect, the infection component, is the means by which the virus will propagate itself and infect other systems.
This model used herein will draw from similarities between computer and biological viruses. The analogy between biological systems and computers has existed since the inception of the computer age. The computer terms ‘bugs’, ‘environment’, ‘worms’, and ‘viruses’ have strong biological connotations and parallels. This is not without reason, as the processes observed in biological systems can represent the processes and mechanisms at work in the artificial environment of computer systems ( Kephart, Chess, & White, 1993 ). The approach finds its promise in that computer and biological viruses exhibit similar behavior ( Thimbleby, Anderson, & Cairns, 1999 ). Both insert themselves into a host, where they produce an undesirable effect. Both use the resources of the host to replicate their genetic or program code and spread themselves to new hosts, thereby spreading the infection. Finally, both the biological organisms and the computers can be immunized against viral infection to the degree that the virus strains can be identified and effectively targeted.
Nevertheless, it is important to be aware of the assumptions of the analogy, since they impact the model’s development. The first assumption is that homogeneous, symmetric interactions take place ( Kephart & White, 1991 ). In biological systems, there is a certain degree of random physical contact associated with the spread of disease. In contrast, in the computer world, physical proximity bears no relevance. In computer communication, interactions are more likely to occur within organizational groups than geographical groups. In both cases, though, the rates of transmission are linked to behavioral patterns. In the computer environment, there are computers that distribute or pass information that other computers download and install and there are servers that send out mass mailings and do not necessarily receive information in return. Similarly, users vary in the degree to which they send and receive files. It should also be noted that there are biological viruses that do not have an equal chance of being transmitted by every host ( Schneeberger et al., 2004 ) and this is likely to be the case for the spread of computer viruses over the entire Internet ( Chang & Young, 2005 ).
Stage 4. Brainstorm/generate model structures
In creating and visualizing the system, a graphical model is structured to match the structure of the system being modeled. System matching approaches provide strong benefits in the classroom, since they allow students to structure their models using personal knowledge. The next stage is identifying the subjects of the model and describing their linkages. In the classroom, exploration of potential structure starts with an inquiry of how the subject of the model can be divided. Each of these divisions or categories will become one of the state variables in this model example. A box will be used to denote each state variable, either the school’s computers or the computer viruses in this example. Students are then asked to identify the pathways where movement can occur between those categories. The paths are indicated by arrows, with arrowhead(s) indicating the directions of the flow. Flows may be either unidirectional or bidirectional.
As shown in Figure 1, there is an array of possible structures for developing the model, depending on how the system is viewed. In diagram (A), the computers are viewed as a group and have been divided based on their infectious state. In this case, computers change status and flow between the boxes representing the various states. This model is a variant of the SIP (susceptible, infected, protected) model used in human epidemiology ( Hannon & Ruth, 1997 ). In diagram (B), the computers have been divided based on the type of users to allow compensation for differences in user behavior. In diagram (C), the computers are arranged based on the network’s topology. In these cases (B and C), the model tracks the movement of the viruses between the computers.
Stage 5. Develop and refine model structures
This stage of designing a model is one of the most difficult to teach, in part because students rarely experience multiple valid choices in their classroom experiences. Unfortunately, in engineering practice and in model development, the luxury of a single solution is seldom available. There is no single “right” model. There are only valid choices.
There are a number of factors that can influence the inclusion or elimination of a model from the overall pool of valid structures. Often, the final, optimal choice is a hybrid of the structures in the initial pool. As with physical design, model development is an iterative process, with decisions to add or remove features of the model occurring continuously. Some methods that are useful in guiding the decisions are:
- Occam’s Razor - ‘ entia non sunt multiplicanda ’ (entities are not to be multiplied without necessity) ( “OED Online”, 2004 ). Using this technique, the simplest model that exhibits the desired behavior is the preferred model. This approach has several justifications. It reduces the amount of data required, the number of assumptions, and opportunities for human or computer error.
- Identification of available information – The data used to build a model or add functionality need to be available and of high quality for the model to be valid. If the information is not available, the model will need to be modified, the missing data acquired, or an estimate of the missing values obtained. All models have limits in their use and these limits are often defined by the data.
- Matching the model to the question – A model that does not answer the question at hand, whether it is accurate or filled with errors, is useless. Many modeling errors are the result of ill-posed questions or specifications. In addition, calibrating or adjusting the model parameters to meet reality and validation, or checking the results against reality, are critical parts of the modeling process ( Haefner, 1996 ).
- Matching the model to the available resources – Time and money are two of the biggest constraints in model building. They often amount to the same thing. In the classroom, time is at a premium and teachers need to balance the time constraints of the course with the levels of refinement of the model. Historically, the resolution and complexity of a model was severely limited by the speed of the available computers, their memory, or the software on which they ran. Fortunately, not only has the software developed and matured, but also the speed of student’s computers is more than adequate for most models.
- Comparing the model’s sophistication and accuracy to that required by the results – Engineering models are often used as the basis for decisions and designs. The time that is spent acquiring quality data and validating a model is dependent on the benefits of getting a right answer and the penalties for failing to get a right answer. Often these benefits/penalties are measured in hundreds of thousands of dollars, jobs, or human lives.
Using one or more of the methods described above, the model’s structure and variables are finalized. While all of the structures in Figure 1 can be made to work, implementing model structures B and C will require that each of their blocks be broken down into a structure similar to that found in structure A. Though B and C are more complex, the additional information that they generate is not required. Therefore A is the most appropriate structure.
In structure A, the overall population of items (the computers) is categorized as having one of three states ( Hoppensteadt & Perkin, 2002 ), each represented by a box in Figure 1A. They are:
- Susceptible Computers (S) – These computers do not currently have the virus and are capable of contracting the virus.
- Infected Computers (I) – These computers are currently infected with the virus and are capable of transmitting the virus to others.
- Protected Computers (P) – These computers are those who do not fall into either of the above populations. Typically, they fall into one or more of the following categories: naturally immune to the virus (running different software), immune to the virus due to immunization (have current antivirus software), and currently infected but not contagious (not connected to the network).
These three variables have values assigned indicating “number of computers.” Mathematically, each state represents a first order differential equation. Using a graphical programming language for implementation, transfers the challenges of writing the equations and their solution to the software, allowing students to concentrate on the structure of the problem and the solution of models that are beyond their mathematical skills.
Computers do not necessarily stay in any one state. If they did, this model would be uninteresting both practically and theoretically. Instead, they are moved from one state to another via the pathways. In this example, four pathways for aggregated changes of the computers’ state will be allowed. By defining the values and constants involved, this model mimics the behavior of the defined virus through a population. The four pathways are:
- Susceptible computers become infected computers (F S-I ) – a virus infects a computer,
- Infected computers become protected computers (F I-P ) – the virus is removed from the computer and the antivirus software is updated,
- Infected computers become susceptible computers (F I-S ) – the virus is removed from the computer, but the antivirus software is not updated, and
- Susceptible computers become protected computers (F S-P ) – current antivirus software is installed on a non-infected computer.
All of these flows are expressed in “computers per day.” Definition of these pathways completes the definition of the model’s structure, and the specific information describing our situation needs to be added.
Stage 6. Implement the model
Next, the model must be converted into a computer program for simulation. In Stella, this conversion is relatively simple. The conversion of the structure is shown in Figure 2A. The next stage in the implementation of the model is identifying the causes and magnitudes of the flow rates. The definitions of the four pathways for flow within this model are shown in what follows.
Infection of a computer by a computer virus. If every host has an equal chance of interacting with any other host, the rate of interaction is proportional to the product of the number of susceptible and infected computers ( Anderson & May, 1991 ). More infected computers and more available susceptible computers result in faster spread of the computer virus. Algebraically, this is:
F S-I = ß • S • I
| Where: | ß = | Infectious contact rate including virus dormancy [1 / (Computers • Day)] |
The contact rate ß is the average number of events of possible transmission per unit of time ( Frauenthal, 1980 ).
Virus removal with installation of antivirus software. The second flow is the flow of individuals from the infected population to the protected. It occurs when a computer has the virus removed and the antivirus software updated. This flow is proportional to the total infected population and the recovery rate following infection divided by the total time from infection to recovery. The recovery rate is the proportion of the infected to be cured and successfully converted to the protected status. The total time is expressed as a latency, ρ, which is the inverse of the time from infection to discovery and the time between discovery and cure, yielding ( Anderson & May, 1991 ):
F I-P = I • Υ • ρ
| Where: | Υ = | Recovery rate [non-dimensional] |
| ρ = | Response latency [1 / Day] |
Virus removal without installation of antivirus software. This flow represents a situation where an infected computer is subjected to a one-time cleaning process without an update to the antivirus software. Thus, the computers in this state are still vulnerable to future virus attack. This flow is proportional to the total infected population and the probability of cleaning the infection without complete immunization from the time of infection to recovery.
F I-S = I • δ • (1 – (Υ • ρ))
| Where: | δ = | Virus protection availability [non-dimensional] |
Installation of antivirus software on an uninfected computer. This fourth flow is an extension of the basic SIP model, and represents the possibility that individuals will learn about a new virus afflicting others and become immunized in anticipation of possible infection, protecting him/her from the virus without having gone through the infected stage. This is particularly appropriate for an academic setting where a single agency administers control over computer laboratories. It assumes that the information upon which action will be taken is proportional to the susceptible population who stand at risk multiplied by the number of individuals who have learned of the virus.
F S-P = α • (I + P) • S
| Where: | α = | Immunization/communication rate [1 / Computers • Day] |
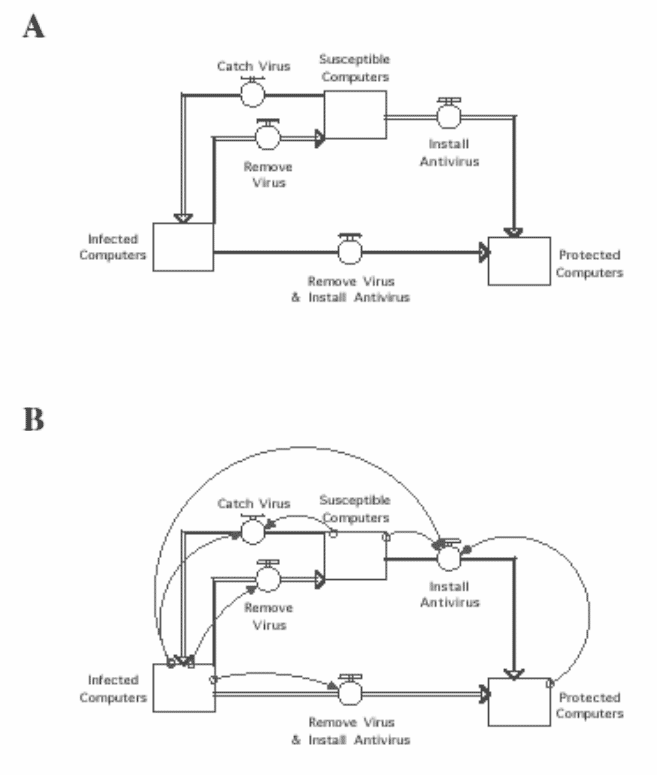
Figure 2. A depiction of the SIP model relationships as implemented in Stella in 2A. The double headed arrow between the susceptible and infected computers in Figure 1A has been replaced by two flow paths because the rate of virus infection and virus removal are different. The SIP model fully implemented in Stella is shown in 2B.
The immunization/communication rate is based on the probability that information concerning the virus will be conveyed to the susceptible population and that the information will be acted upon.
The coupled differential equations describing this model are shown in Table 3. These equations are known as the state equations for the model. In aggregate, they describe the changes to the state variables.
| State Variable | Assembled Differential Equations |
|---|---|
| Susceptible Computers |
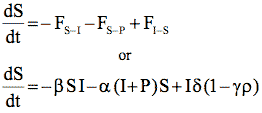
|
| Infected Computers |
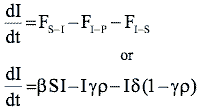
|
| Protected Computers |
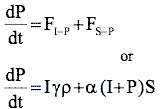
|
Stage 7. Specify and simulate
The final step before actually running any model is entering the specific values describing the situation of interest. The example model requires three initial conditions, shown in Table 4, and five rate coefficients specifying the flows between the states, shown in Table 5. The initial conditions assume that the computers are largely unprotected against the virus, as would occur with a new virus. The rate constants describe a rapidly spreading virus and a very rapid response by the generator of the antivirus software and the computer technicians at the school.
| State Variable | Symbol | Number of Computers |
|---|---|---|
| Susceptible | S | 195 |
| Infected | I | 2 |
| Protected | P | 3 |
| Total Number of Computers | 200 |
| Coefficient | Symbol | Value |
|---|---|---|
| Infectious contact rate | β | 0.15 |
| Recovery rate | Υ | 0.10 |
| Response latency | ρ | 0.33 |
| Virus protection availability | δ | 0.25 |
| Immunization rate | α | 0.05 |
The assembled model after the implementation of the equations and the inclusion of the initial conditions and rate constants is shown in Figure 2B. In addition, the results of this simulation are shown in Figure 3.
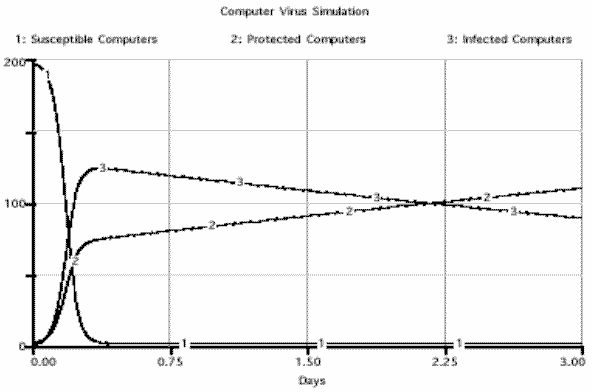
Figure 3. The results of the simulation produced by Stella. The simulation shows a rapid decline in the number of susceptible computers with concomitant rises in the number of protected and infected computers. Later, the number of infected computers decreases as their viruses are removed and protective software is installed. The simulation was performed using a numerical integration with a step size of 0.01. The integration was performed using a 4 th -order Runga-Kutta.
Stage 8. Interpret and communicate
Once a model is complete, it will be used, often by those who did not design it. Full documentation is an essential component of any design process. Typically, this documentation will include:
- Identification of all components, assumptions, and limitations of the model,
- Documentation of the software under which the model operates, and
- Printouts of the model and typical results.
It is worth noting that models are also intellectual property. Complete documentation should include the filing of documents to protect that property. This protection is an important business issue. Consulting firms sell the results of their simulations and, as noted earlier, many computer games contain significant computer modeling components. To put it in perspective, one major computer games company, Electronic Arts, had a net revenue of 1.3 billion dollars for the final quarter of 2005 ( Tamaki, 2006 ).
Stage 10. Perform post-implementation review
In addition, the modeler needs to understand that the model that has been created will need to be updated or modified. In our example, a new virus may emerge with different properties. New computers may be added to the school. The school district may want to understand the impact of the virus on all of the schools under its control. In the case of computer models of electronics, new parts will become available. In the case of computer games, a new version of the game will need to be created.
An important component of any design process is the evaluation review that should occur after the model has been completed. There are three broad categories that need to be considered, including
- What did we do right?
- What did we do wrong?
- How can we improve our process?
The modeler will generally be asked to create new models in the future and modify the present model. Understanding the successes and failures of the process used to create the model will result in a smoother, more efficient design process the next time it is performed. A useful analogy is that of the toolbox. Each model adds techniques to the engineer’s or designer’s toolbox. The post-implementation review helps the modeler to understand the strengths and limitations of their tools.
Conclusions and Implications
The ten-stage modeling paradigm represents a method for the development of engineering models. It adapts a design paradigm used in technology education for the creation of these models. Furthermore, instead of requiring the development of computer code in Basic, FORTRAN, or other manual analytical solution for simultaneous differential equations, this approach graphically develops the structure of the model and implements the model in graphical modeling software. By defining state variables and the flows into and out of the variables using algebraic equations, complex engineering models can be developed and solved in high school classrooms.
The introduction of design-based methodology for graphical model development has a number of implications for technology education. First, it builds on the historical strengths of technology education such as hands-on experiences, visualization, and design and uses those approaches to bring relevance to students’ mathematics and science skills. Further, this is achieved by meeting the goals of the Standards for Technological Literacy ( ITEA & TAAP, 2000 ) through application of the content of the National Science Education Standards ( National Research Council [U.S.], 1996 ) and the Principles and Standards for School Mathematics ( National Council of Teachers of Mathematics, 1989 ). Second, it teaches the transferability of the design process to other disciplines by following paradigms that are familiar to both students and the teachers of technology education. This familiarity reinforces the design paradigms in the students’ minds, while extending their abilities. Finally, by using software to create and solve the mathematical models that are constructed, the approach is less dependent on the abilities of the students to perform mathematical manipulations. In fact, it is relatively easy to create and solve mathematical models that are analytically insoluble even for many practicing engineers.
References
Anderson, R. M., & May, R. M. (1991). Infectious Diseases of Humans Dynamics and Control. New York, NY: Oxford University Press.
Best of What's New 2005. (2005). Popular Science, 267 (6), 29.
Chang, D. B., & Young, C. S. (2005). Infection dynamics on the Internet. Computers & Security, 24 (4), 280-286.
Coughanowr, D. R., & Koppel, L. B. (1965). Process Systems Analysis and Control. New York: Mc-Graw Hill Book Company.
Eggert, R. J. (2004). Engineering design. Upper Saddle River, NJ: Pearson Prentice Hall.
Feynman, R. P. (1998). The meaning of it all: Thoughts of a citizen-scientist. New York, NY: Basic Books.
Fisher, D. M. (2005a). Lessons in mathematics: A dynamic approach. Lebanon, NH: ISEE Systems.
Fisher, D. M. (2005b). Modeling dynamic systems: Lessons for a first course. Lebanon, NH: ISEE Systems.
Frauenthal, J. C. (1980). Mathematical modeling in epidemiology. New York, NY: Springer-Verlag.
Gomez, A. G., Oakes, W. C., & Leone, L. L. (2004). Engineering your future: a project-based introduction to engineering. Wildwood, MO: Great Lakes Press.
Gotelli, N. J. (1998). A Primer of Ecology (Second ed.). Sunderland, MA: Sinauer Associates, Inc.
Haefner, J. W. (1996). Modeling biological systems: Principles and applications. New York, NY: Chapman & Hall.
Haik, Y. (2003). Engineering design process. [South Melbourne, Victoria], Australia ; Pacific Grove, CA: Thomson/Brooks/Cole.
Hannon, B. M., & Ruth, M. (1994). Dynamic modeling. New York: Springer-Verlag.
Hannon, B. M., & Ruth, M. (1997). Modeling dynamic biological systems. New York: Springer.
Hoppensteadt, F. C., & Perkin, C. S. (2002). Modeling and simulation in medicine and the life sciences (2nd ed.) . New York, NY: Springer-Verlag.
International Technology Education Association, & Technology for All Americans Project. (2000). Standards for Technological Literacy: Content for the study of technology. Reston, VA: International Technology Education Association.
Kephart, J. O., Chess, D. M., & White, S. R. (1993). Computers and epidemiology. IEEE Spectrum(May), 20-26.
Kephart, J. O., Sorkin, G. B., Chess, D. M., & White, S. R. (1997). Fighting computer viruses: Biological metaphors offer insight into many aspects of computer viruses and can inspire defenses against them. Scientific American(November), 88-93.
Kephart, J. O., & White, S. R. (1991). Directed-graph epidemiological models of computer viruses. Paper presented at the IEEE Computer Society Symposium on Research in Security and Privacy, Oakland, CA.
Kim, K.-J., & Cho, S.-B. (2006). A comprehensive view of artificial life. Artificial Life, 12(1), 153-182.
Koen, B. V. (2003). Discussion of the method: conducting the engineer's approach to problem solving. New York: Oxford University Press.
Kurzweil, R. (1999). The age of spiritual machines: when computers exceed human intelligence. New York: Viking.
Lewis, P. H., & Yang, C. (1997). Basic control systems engineering. Upper Saddle River, NJ: Prentice Hall.
National Council of Teachers of Mathematics. (1989). Principles and standards for school mathematics. Retrieved February 15, 2006, from
standards.nctm.org/document/appendix/alg.htmNational Research Council (U.S.). (1996). National Science Education Standards: observe, interact, change, learn. Washington, DC: National Academy Press.
Oakes, W. C., Leone, L. L., & Gunn, C. J. (2004). Engineering your future: a comprehensive approach (4th ed.). Wildwood, MO: Great Lakes Press.
OED Online. (2004, August 1). Retrieved December 22, 2006, from
http://dictionary.oed.comOgata, K. (1997). Modern control engineering (3rd ed.). Upper Saddle River, N.J.: Prentice Hall.
Phillips, C. L., & Harbor, R. D. (1996). Feedback control systems (3rd ed.). Englewood Cliffs, N.J.: Prentice Hall.
Project Lead the Way. (2006). General FAQ's. Retrieved January 1, 2007
Richmond, B. (2004). An introduction to systems thinking. Lebanon, NH: ISEE Systems.
ROBO Pro. (2005). (2005). Erbes-Büdesheim, Germany: Fischertechnik GmbH.
Robolab. (2004). (2004). Medford, MA: Tufts University.
Schneeberger, A., Mercer, C. H., Gregson, S. A., Ferguson, N. M., Nyamukapa, C. A., Anderson, R. M., et al. (2004). Scale-free networks and sexually transmitted diseases: a description of observed patterns of sexual contacts in Britain and Zimbabwe. Sexually Transmitted Diseases, 31 (6), 380-387.
Simulink. (2005). [Graphical Modeling]. Natick, MA: Mathworks, Inc.
Stella. (2005). [Systems Modeling]. Hanover, NH: ISEE Systems, Inc.
Tamaki, J. (2006, February 3). EA profit slides 31% as gamers opt to wait. Los Angeles Times.
Terzopoulos, D. (1999). Artificial life for computer graphics. Communications of the ACM, 42 (8), 33-42.
Thimbleby, H., Anderson, S., & Cairns, P. (1999). A framework for modeling trojans and computer virus infection. Computer Journal, 41 (7), 444-459.
Zahnley, T. (2006). Berkeley Madonna (Version 8.3). Berkeley, CA: Berkeley Madonna.
____________________
Paul D. Schreuders ( pschreuders@cc.usu.edu ) is Assistant Professor in the Department of Engineering and Technology Education at Utah State University , Logan, Utah.