Abstract
The introduction of engineering practices within the Next Generation Science Standards provides technology educators with opportunities to help STEM educators infuse engineering design within a core curriculum. The introduction of teaching engineering design in early elementary grades also provides opportunities to conduct research investigating how young students use engineering design as a way to solve problems. There is a need for research to assess how students experience engineering design as a pedagogical approach to learning science. This article will feature research on elementary students' cognitive strategies used during engineering-design science activities. We adopted the concurrent think-aloud (CTA) protocol analysis method to capture how students conceptualize design and enhance science learning. During the 2012-2013 school year, we video recorded 66 CTA sessions, and this study examines six of those sessions. NVivo (Version 10) was used to code each video using common cognitive strategies categorized by Halfin (1973) . Research findings indicate that participants increased the amount of time spent on mathematical thinking by 34% when given a math-specific design task. Pre- and post-tests showed that participants gained significant science content knowledge. However, we also confirmed that participants struggled with applying accurate mathematical and scientific knowledge to solving the given design problem.
Keywords : concurrent think-aloud protocol; design cognition; transfer of learning
Design is a core component of technology education ( Lewis, 2005 ). Engineers, designers, and others in technology design and create solutions to given problems. Therefore, technology educators have been implementing the engineering-design approach as an effective way to teach technology. Although technology education is putting greater emphasis on engineering design ( Hill, 2006 ; Lewis, 2005 ; Wicklein, 2006 ), recently, K-12 science education in the United States has proposed the teaching of engineering practices alongside the teaching of science practices. For example, the Framework for K-12 Science Education ( National Research Council [NRC], 2012 ) includes engineering-design learning standards. The framework provides a strong platform for teaching engineering and technology contexts to enhance students' science learning. The document states:
Engineering and technology provide a context in which students can test their own developing scientific knowledge and apply it to practical problems; doing so enhances their understanding of science-and, for many, their interest in science-as they recognize the interplay among science, engineering, and technology. We are convinced that engagement in the practices of engineering design is as much a part of learning science as engagement in the practices of science [(National Academy of Engineering and National Research Council, 2009)]. (p. 12)
Many states, including Massachusetts and Minnesota, have created academic standards requiring students to engage in the engineering-design process and to explore the nature of technology and engineering practices within science standards (Robelen, 2013). Conceptually, the driving force behind these educational reforms is the emphasis on students developing the abilities to define problems by asking questions, create and apply models, generate plans, engage in design challenges, and apply evidence-based scientific knowledge to create and select the best possible solution to a problem ( NRC, 2012 ).
With the introduction of the Next Generation Science Standards to the elementary science classroom, technology educators can use their long history of design study in the secondary grade level to investigate the use of engineering design with elementary students. This will provide technology educators with a better understanding of how young students solve problems using the engineering-design approach. In addition, technology educators have shown that engineering design not only enhances STEM teaching and learning but also helps students develop cognitive capabilities by practicing engineering design as a problem-solving strategy ( Lammi & Becker, 2013 ).
One measure used to investigate students' cognitive approaches is the think-aloud protocol. Atman and Bursic (1998) employed the think-aloud protocol method as an evaluation tool to assess students' design and problem-solving capacity. They used it to understand how undergraduate engineering students solved open-ended, ill-defined engineering-design problems. Similar to Atman and Bursic's studies, this study used a concurrent think-aloud (CTA) protocol in an elementary setting to inform technology education and STEM education about how elementary students solve design problems.
As a part of Science Learning through Engineering Design (SLED), a Math Science Targeted Partnership (MSP) funded by the National Science Foundation (NSF), we conducted two studies in which we collected data from CTA sessions to measure students' problem-solving ability. In the first study, data were collected on Cohort 1 in the 2011-2012 school year. In the second study, which is the subject of this article, data were collected on Cohort 2 in the 2012-2013 school year.
In the original study of Cohort 1, we collected data from 33 CTA sessions to measure the students' problem-solving ability in the 2011-2012 school year. Key features of engineering-design thinking often require many cognitive strategies; however, in the findings from Cohort 1, students showed limited use or no use of these strategies. The Cohort 1 findings revealed that the students spent very little time in computing (4%), managing (1%), testing (3%), and predicting results (4%). Students spent almost half of their time generating ideas (47%). CTA sessions from Cohort 1 indicate that student teams (triads) did not emphasize the use of computing (CO) and testing (TE) during the protocol sessions. Additionally, the cognitive strategy interpreting data (ID) was missing from all the protocol sessions. Even though mathematical reasoning skills such as computing, testing, and interpreting data are the key elements of engineering design, the results indicate that students were not using these skills. The results of the Cohort 1 study are compared with those of Cohort 2 in the Results section.
Purpose of the Study
The purpose of this study was to investigate how triads of students collaboratively developed solutions and applied scientific and mathematical concepts to inform their solution to engineering-design challenges. The questions guiding this study included the following:
- How do Grade 5 students conceptualize and learn design?
- Which aspects of the engineering-design process do students tend to emphasize?
- Which aspects of the engineering-design process do students tend to overlook?
- To what extend do students apply scientific concepts and mathematical reasoning when engaging in an engineering-design transfer problem?
Theoretical Perspective
The theoretical perspective for studying participants' cognitive strategies through design is based upon the construct of transfer of learning ( Bransford, Brown, & Cocking, 1999 ). Transfer of learning suggests that students can transfer their prior knowledge, skills, and experiences to new situations. When students are presented with new opportunities that are similar to pre-existing experiences, learning transfer can occur. Learning transfer is an indicator of understanding. Royer (1986) further describes the concept of transfer of learning: "Used as an index of understanding is equivalent to the idea that the ability to transfer learned information is evidence that understanding is present" (p. 95). In this study, we carefully crafted transfer problems that were similar in structure and scope to those presented to the students during a prior learning experience in order to assess a near transfer of learning ( Thorndike, & Woodworth, 1901 ; Bransford, et al., 1999 ). We observed and coded student dialogue to determine if students transferred what they had learned during the SLED activities to the transfer problems. Specifically, we were looking for students to transfer key engineering and science practices, scientific concepts, and the use of mathematical reasoning.
Literature Review
A CTA protocol is a procedure that allows a researcher to study the verbal report of one individual or group of individuals speaking their thoughts while engaging in an assigned task or problem. Recently, the CTA method has been applied to a wide variety of contexts, such as studying human operations of process controlling systems ( Sanderson, Verhage, & Fuld, 1989 ), cognitive studies on writing ( Ransdell, 1995 ) and reading ( Pressley & Afflerbach, 1995 ). CTA protocols are endorsed as a promising tool to capture cognitive and metacognitive thinking in engineering education research (Atman & Bursic, 1998). Multiple CTA studies have investigated engineering-design approaches within engineering education ( Atman, Chimka, Bursic, & Nachtmann, 1999 ; Atman, Cardella, Turns, & Adams, 2005 ; Gainsburg, 2015 ) and team-based engineering design and problem solving ( Mentzer, 2014 ; Stempfle & Badke-Schaub, 2002 ).
However, investigating the cognition of designers during design is challenging. Ericsson and Simon (1993) suggest that CTA methods may provide the most authentic approach to achieve a record of cognitive activity during design because the designer is allowed to perform in his or her natural state of mind not altered by outside influences beyond verbalizing thoughts. Unlike structured elicitation approaches to cognitive investigations, CTA investigation seeks to place the participant in his or her most natural state of design thinking during the protocol sessions ( van Someren, Barnard, & Sandberg, 1994 ).
Some questions have arisen regarding CTA as a proper method to capture all aspects of design cognition. Lloyd, Lawson, and Scott (1995) reported that CTA methods may accurately capture short-term thought processes but fail to capture long-term states of memory. However, allowing designers to express ideas graphically allows for both short-term and long-term cognition ( Ullman, Wood, & Craig, 1990 ). In addition, the CTA method requires participants to use their own language and to approach the assigned task as they would naturally solve it. Furthermore, some researchers questioned the validity of CTA data from young children. However, van Someren, Barnard, and Sandberg (1994) found that
In our experience, the quality of verbalizations is not strongly associated with other properties that can easily be observed or measured. One possible exception is age. Young children usually find it difficult to think aloud. It is not clear if this is due to their verbalization skills, to the content of their thought processes or to the general difficulty of concentrating on a problem-solving task. (p. 35-36)
In a usability study, Donker and Markopoulos (2002) stated: "We expected methods like think-aloud that require high verbalization skills to be less effective for younger children or children with fever verbalization skills. Our expectations were not confirmed" (p. 314). We acknowledge these possible limitations of CTA protocols and, therefore, provided participants with the opportunity to create design sketches during the protocol sessions and to allow participants to work collaboratively and in their most natural state.
Research Design
Context of the Study
This study is part of an NSF-funded MSP entitled SLED (for more information, see https://stemedhub.org/groups/sled). The collaborative partnership is made up of four colleges within a large, research-intensive university and four school corporations located in the north-central Midwest. The primary goal of the SLED project is to improve achievement in Grades 3-6 students' science learning through an engineering-design pedagogical approach. Over the course of 5 years, approximately 100 pre-service teachers, 200 in-service teachers, and 5,000 students in Grades 3-6 will participate in the partnership.
This research study was drawn from two SLED partnership schools. School Site 1 was located in an emerging urban school district, and School Site 2 was located in a rural fringe school district (see Table 1 for demographics).
| Category | School Site 1 | School Site 2 |
|---|---|---|
| Enrollment | 552 | 124 |
| Ethnicity | ||
| White/Caucasion | 56% | 76.6% |
| Hispanic | 27.7% | 12.1% |
| Black/non-Hispanic | 10.1% | 4.8% |
| Asian | 0.4% | 0.0% |
| Multiracial | 5.1% | 5.6% |
| American Indian | 0.5% | 0.8% |
| Free or reduced-price lunch | 71.9% | 43.6% |
Student Design Activities
In the second year of the project, the design team developed two math-embedded SLED activities to provide students' mathematical reasoning practice. These activities were also designed to address science standards. The activities were (a) the CO2 Device activity in which student designed a device utilizing a balloon filled with carbon dioxide and (b) the Recycling Paper activity. Table 2 gives an overview of the design activities (see Appendices A and B for the design activity prompts). The series of science lessons implemented to support the engineering-design tasks was between five to seven 45-minute lessons delivered by SLED teachers. These science inquiry lessons contained the science content knowledge required to successfully complete the engineering-design tasks. These lessons targeted students' misconceptions regarding conservation of mass, which have been documented by Driver (1983) and Driver, Squires, Rushworth, and Wood-Robinson (1994) .
| Title | CO 2 Device | Recycling Paper |
|---|---|---|
| Description | The CO 2 device activity required students to design a device utilizing a balloon filled with carbon dioxide generated from mixing vinegar and baking soda. | The recycling paper activity involved students calculating the volume and mass of an irregular material (pile of shredded paper) or mixture of paper and water (sludge) while designing a process to make recycled paper. |
Participants
During the 2012-2013 school year (Cohort 2), we collected data from a total of 66 CTA sessions. Analysis of data from the 66 sessions provided general design patterns of the cognitive approach that students took in the engineering-design challenges. Data from six sessions were further analyzed to understand how students used cognitive strategies to solve math-embedded design problems.
We used criterion sampling to select cases that satisfied a specific criterion ( Gall, Gall, & Borg, 2007 ). Participants for the think-aloud protocols were purposefully selected by the SLED teachers. Teacher recommendations were based upon (a) the students' ability to express themselves verbally, (b) their ability to successfully function as contributing members of a design team, (c) their assent to participate in the study, and (d) parental consent for the students to participate. Triads of student design teams were formed for each SLED classroom participating in the research. Welch (1999) suggests that pairing or grouping student participants allows for the design process to emerge naturally because most design efforts occur in groups of two or more people working together. Table 3 lists the total classroom size and genders of the three students selected as part of the triad for the six case studies. For example, Classroom 1 had a total of 54 students, and one male student and two female students were selected to form a triad.
| School Site 1 | School Site 2 | |||||
|---|---|---|---|---|---|---|
| School | Classroom 1 | Classroom 2 | Classroom 3 | Classroom 4 | Classroom 5 | Classroom 6 |
| Classroom Size | 54 | 55 | 48 | 59 | 30 | 29 |
| Student Gender | 1M, 2F | 2M, 1F | 2M, 1F | 1M, 2F | 2M, 1F | 2M, 1F |
Data Collection
Concurrent think-aloud protocol. The study employed the CTA protocol to capture students' cognitive thinking processes and thoughts. After each participant classroom completed the SLED design activity, we selected a triad of students to participate in the CTA protocol. According to the Ericson and Simon's (1993, p. 18) suggestion for CTA data collection, we provided students with two guidelines: (a) explain their thoughts directing their attention to the problem-solving procedure and (b) utilize their prior knowledge from the classroom-based design activity to the transfer problem presented in the protocol session.
Transfer problem. The transfer problem was a key instrument used to provide each triad with the opportunity to study design problems similar to the SLED design activities. As Cross (1994) suggested, transfer problems consist of three parts: (1) a goal, (2) constraints to address, and (3) design criteria to gauge the final design solution against. In this study, we focused on creating authentic engineering-design problems that required the use of science concepts embedded within the task. The problem scenarios were created based on situations that students might encounter in their daily lives or on designing products that were familiar to them. One transfer problem, Scotty's Scooters in Appendix C, was created for both the Recycling Paper and the CO2 Device tasks because they addressed the same science concept, conservation of mass.
SLED knowledge assessments. To investigate the gap between knowing and applying scientific knowledge, we adopted a set of pre- and post-knowledge tests. Using an approach similar to Singer, Marx, Krajcik, and Chambers (2000) and Fortus, Dershimer, Krajcik, Marx, and Mamlok-Naaman (2004) , we constructed a multiple-choice test that contained items of low, medium, and high cognitive demand to assess students' preexisting knowledge and to measure gains in knowledge. As Fortus et al. (2004) described, in order to get accurate indication of student's growth in knowledge from the SLED activities, researchers must first determine what students already know about the science. Pretest assessments were administered at the start of the academic year, and posttests were administered within 10 days of completing the SLED activity. Because one of the participants was absent when the pretest assessment was administered, pre- and post-test scores were only available for 17 participants.
Data Analysis
Think-aloud protocol analysis. The study adopted Halfin's (1973) codes to analyze the think-aloud data. These codes were created during Halfin's Delphi study that researched commonly used cognitive strategies by successful professional scientists, engineers, and inventors. Seventeen cognitive strategies were generated, and detailed descriptions were developed from the research and validated by 28 panel members. One advantage to using Halfin's codes for this analysis is that it provides problem-solving processes as well as comprehensive cognitive strategies usually used in design activities. Halfin's coding scheme allowed us to investigate students' abilities to apply their design and problem-solving capabilities to transfer problems ( Hill, 1997 ; Kelley, 2008 ; Kelley, Capobianco, & Kaluf, 2015 ; Wicklein, 1996 ).
Interrater reliability of think-aloud analysis. Several steps were followed to ensure interrater reliability when analyzing the video data. First, two researchers carefully reviewed the coding scheme and definitions created by Halfin (1973, pp. 135-204) and mapped students' dialogues to these codes. Seven codes were determined to be outside the parameters of the protocol sessions, so these codes were removed from the coding list for the purpose of this research. 1 As a result, we utilized 10 of the 17 codes developed by Halfin (1973). The 10 codes used in this study are described in Appendix D. Second, sample video clips were viewed by the two researchers together, and their interpretations of the selected segments were discussed in order to reach coding consensus. Finally, the two researchers independently coded the video segments, and their analyses were compared. The kappa coefficient for interrater reliability was calculated. Hruschka et al. (2004) suggested that at least 20% of the data set results should be compared between two independent researchers. In this study, we analyzed one third of the CTA sessions to ensure interrater reliability. Each video from the six CTA sessions was segmented into three parts, and one segment from each session was analyzed for interrater reliability. To achieve acceptable levels of intercoder reliability, we followed Hruschka et al.'s iterative coding method (p. 311), and a Kappa coefficient of 0.91 was calculated using NVivo (Version 10) with 99.45% agreement.
SLED knowledge assessments analysis. In order to measure that participants successfully gained scientific and mathematical knowledge through the SLED engineering-design lessons, we compared pre- and post-test scores using a paired sample t-test using SAS (Version 9.4), a statistical analysis software.
Results
Concurrent Think-Aloud Protocols
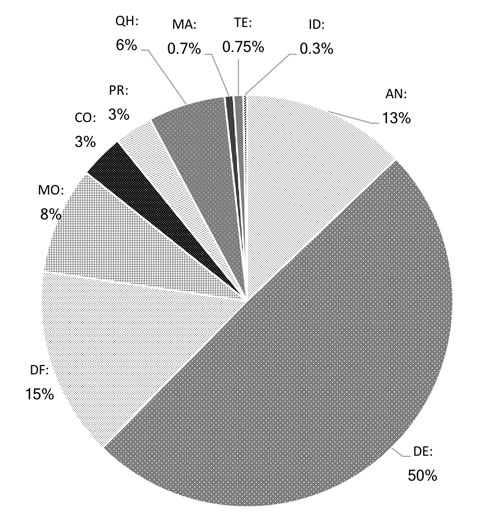
Data from 66 concurrent think-aloud protocols were collected during the 2012-2013 school year (Cohort 2). The mean percentages for the coded sessions are displayed in Figure 1.