SPT v13n2 - Structure and Coherence of Two-Model-Descriptions of Technical Artefacts
Structure and Coherence of Two-Model-Descriptions of Technical Artefacts
Ulrich Krohs
Department of Philosophy, University of Hamburg,
and
Konrad Lorenz Institute for Evolution & Cognition Research, Altenberg
Abstract
A technical artefact is often described in two ways: by means of a physicalistic model of its structure and dynamics, and by a functional account of the contributions of the components of the artefact to its capacities. These models do not compete, as different models of the same phenomenon in physics usually do; they supplement each other and cohere. Coherence is shown to be the result of a mapping of role-contributions on physicalistic relations that is brought about by the concept of function. It results a sandwich-like structure of the two models, which can be reconstructed as a two-sorted theory element.
Keywords: Theory structure, Theory element, Function, Transistor
A technical artefact may be described in physicalistic and in functional terms. The physicalistic description accounts for structure and dynamics of the entity, while the functional description is based upon a design-and-use-centred view of the artefact. Both descriptions belong to different areas of knowledge and the question is how they cohere. Regarding the different descriptions as different models of the same entity, this question for coherence becomes a question of theory relation, i.e., of the relation between both models. To investigate this relation, I am splitting the problem of coherence into two questions. The first one is the question for consistency of the models. Though small inconsistencies would not completely corrupt coherence, they would diminish it and we should not presuppose that descriptions of technical artefacts are usually inconsistent. Consistency is reflected in theory structure, so the task is to reconstruct the structure of the “sandwich” of a physicalistic and a functional model and look whether it is consistent. Consistency alone, however, does not bring about coherence. Obviously, the junction of two isolated sets of propositions is consistent, but it would be strange to call this junction, which falls in two, coherent. Isolation has to be regarded as a feature that diminishes coherence ( BonJour 1985, p. 95). Some relation must hold between the elements of physicalistic and functional descriptions that brings coherence about. Laurence BonJour regards mainly inferential relations between the elements of a class of propositions as increasing its coherence (op. cit.). According to Paul Thagard, among the candidates for such relations are explanatory and deductive relations as well as other mappings (e.g., Thagard et al. 2002 ). So the second task is to inquire into the kind of relation that holds between a physicalistic and a functional model and show how this relation accounts for the coherence of the description that is made up by a combination of both models.
The required concepts for the reconstruction are introduced in the first section of this paper. The second section develops the structure of consistent two-model-descriptions. The third section is dedicated to the question of coherence of physicalistic and functional models. In the fourth section, I will demonstrate the application of my reconstructive approach to the case of the transistor. I will then discuss how this approach deals with the ambiguity of structure-function relations, and finally sum up my results.
1. Theory relations and sorts of models
The case of physics
Most investigations of theory relations have concentrated on physical theories. When two different models are given for the same process, in physics the question is usually: which is the better one? “Better”, of course, needed to be qualified and may be relative to some epistemic goal. Even if there is no ranking among the models, they are in most cases alternatives, not supplements. A description may use one model or the other, but one cannot combine both without running into inconsistency. For example, classical and relativistic mechanics cannot be mixed up. However, one of the models may be reduced to the other. This means that it is possible either to express all that can be said by the reduced model in terms of the reducing one, or at least to map all results of one model onto the results of the other. In terms of Scheibe’s synthetic concept of reduction (
Scheibe 1993,
p. 266), we have a
partial reduction
in the latter case.
1
Nevertheless, since such a mapping of results may hold even with inconsistent models, reducibility is not a guarantee for the consistency of two theories.
There is a case in physics in which the competition between two models is set aside and instead two seemingly incompatible models are used in parallel without a reduction relation holding between them: the case of the dualism of wave and particle descriptions of elementary particles. Neither model is sufficient for the description of all phenomena observed. Therefore both are used, as a workaround, in parallel. But in this case, both models have different ranges of application, which prevents inconsistency. So this is not a paradigm for cases like those that shall now be discussed.
The case of biology and of technology
If we look at biology, things turn out different. Here, we have two different sorts of models: physicalistic models that describe the physicochemical mechanisms of biological processes and functional models that describe the various mechanisms as realizing physiological functions. The functional account is normative since it allows for judgments about whether a component of a system behaves as it is supposed to do. So function modules are of another sort than physicalistic ones. While this characterization of the model sorts classifies models according to the involvement of functional terms, I have proposed an independent delineation criterion elsewhere (
Krohs 2008
).
The case of technology is similar to that of biology. Physicalistic models of technical artefacts, i.e., descriptions of the physical processes going on within an artefact, and functional models that describe these processes as being implemented to follow a certain goal, complement each other. Both descriptions are required and technical artefacts, if described only in terms of their physical properties not also from the functional perspective, would become mere physical objects and would lose their status as technical entities ( Kroes 2002, p. 294).
Since the cases of modelling biological and technical systems both show the duality of physicalistic and functional views, many of the results that were obtained in philosophy of biology are also valid for the technological case. This holds in particular for the debate about reductionism. There was an extensive discussion of the question whether biology in general can be reduced to physics. 2 However, up to now all attempts failed and reduction cannot be regarded as a general means to eliminate functional talk, one of the main obstacles being the multiple realisability of functions ( Putnam 1967; Fodor 1974 ). 3 One way to escape from unsuccessful reductionism is to regard functions as emergent properties of technical and biological systems and base the analysis of functional models on strong concepts of emergence (see, e.g., Beckermann et al. 1992 ). Reference to emergent properties, however, would be a way out only if functionalities were adequately conceived as properties. But they are categorically different from properties in being normative: a function may still be correctly ascribed even if the function bearer is dysfunctional and thus unable to perform the function. 4 I therefore treat functionalities not as properties but as theoretical terms of the functional models that we use to describe biological organisms. Functional models have consequently to be conceived as being of a different sort than physicalistic models. Biological theories, then, are composites of models of both sorts. The strategy to investigate the interplay of models of different sort is to reconstruct the structure of such composite theories ( Krohs 2004, chs. 7-8).
It is important to notice that a functional model of a technical artefact is not only an incomplete version of a physicalistic one. It makes use of classifications (like: being a signal or a force-generator) that cannot occur in a physicalistic model but are genuinely technical, i.e., related to design, use, or technical function of an artefact. Only the different carriers of a signal can occur in the physicalistic model. And only a functional model may be used to refer to malfunction, since this requires some kind of norm that discriminates function from malfunction – there is no such normativity in a physicalistic model. We have two non-exclusive possibilities by which to model these devices: a physicalistic model, and a functional model. Neither of them alone covers all that can be known about a technical artefact.
2. Theory structure: Consistency
To examine the coherence and consistency of mixed physicalistic/functional theories, the different models have to be described uniformly, i.e., they have to be reconstructed to some degree. For the present purpose, the structuralist version of model theory as developed by Sneed ( 1971 ) and refined by Stegmüller and co-workers ( Balzer et al. 1987 ) seems to be the most adequate method of reconstruction. It starts from the assumption that the reconstructed models are not universally applicable but only locally, in an intended range of applications (which may be modified whenever new and adequate applications are found). This spares a lot of caveats, which were needed with a global approach like van Fraassen’s constructive empiricism ( van Fraassen 1972 ). So my decision to use structuralism is not based on any special “structuralist theory conception” that would claim that some theories have a structuralist structure ( Stegmüller 1986, p. 3). I regard structuralism just as one of several tools to reconstruct theories and theory relations, and feel that it is for my purpose the most convenient of the presently available tools.
The approach
I will use a few concepts of structuralism only and will confine myself to introducing only these instead of the whole apparatus. Moreover, my version is a simplified version of structuralism.
Talking about models in the sense of structuralism, a second concept of a model has to be used that differs from the one used in science and in technology. A model in the structuralist sense is a mathematical structure, i.e., a set of objects with relations defined on it. (We can ignore for the present purpose that, strictly speaking, we would have to deal not with structures but with classes of isomorphic structures.) The structure itself, i.e., the mathematical model, is not yet the reconstruction of a technical description or of a scientific model, since it does not by itself apply to any phenomenon; it is not a model of anything. What is needed in addition is the specification of the intended phenomena the mathematical model has to be applied to. Therefore, the model (or class of models) in the structuralist sense plus a class of intended applications makes up the smallest piece of theory or of description. This piece is called a theory element. A theory element, not a model in the mathematical sense, is the structuralist equivalent to a scientific model or to a technical description. For example: the mathematics of the Kepler laws defines a structure only. To turn this into a model of the dynamic of components of the solar system, we have to add that this structure is intended to describe this very dynamic, which is done in the definition of the variables. Moreover, we will not reject the Kepler laws just because they fail when applied to raindrops or to billiard balls. Instead, we simply leave these possible applications outside the class of intended applications of the laws. Only the model plus the intended applications allow for scientific explanation and make up a theory element.
I will refer in my argument to the following constituents of a theory element: a basis O which is the set of objects the theory element deals with and a set R of relations defined over O . These two classes make up the core of a theory element and define the notions that are available within a particular element. O specifies what can be called the ontology of the theory, and R specifies the properties of the elements of O . In addition, there is the set I of intended applications of the theory core. 5 So, a theory element can be characterised as ( Balzer et al. 1987 ):
T = 〈 O, R, I 〉.
Two-sorted theory elements
A theory element as characterised by
I, O,
and
R
may be the reconstruction of any scientific model or technological description, be it of physicalistic or of functional sort. The sort depends on the elements of
R
, which may be physical or functional relations. The crucial question is how to represent the interaction of a physicalistic and a functional model. I have introduced the notion of a
two-sorted theory element
to analyse this case (
Krohs 2004
).
A two-sorted theory element shall be conceived as a theory element that combines two “matching” models of the same phenomenon and has greater explanatory power than either of the two models standing alone. Not any arbitrary pair of models meets this requirement. The application of the concept has to be restricted to pairs of models that are (i) of different sort, that are (ii) models of the same entity or phenomenon and that (iii) describe the same aspect of this entity or phenomenon. I call two models that satisfy these requirements a pair of corresponding models. Satisfaction of condition (i) (sort-difference) is given in all cases where a physicalistic and a functional model are combined. Condition (ii) (identity of the described entity or phenomenon) is satisfied by any pair of sort-different models that share the same basis O. However, there will usually be some differences in the bases, with a large intersection. The basis of the two-sorted theory element is the union of both bases. The overlap is significant in all cases in which it can be assumed that the modellers do regard a physicalistic and a functional model as referring to the same entity or phenomenon (e.g., the description of an integrated circuit as a set of logic gates and as a collection of semiconductors with certain electrical characteristics that bring the logical functions about; the biochemical and the information-transfer model of protein biosynthesis). Condition (iii), asking for identity of the aspect described, rules out cases in which one aspect of the entity or phenomenon is described in a physicalistic way, and another aspect in a functional way. For example, a physicalistic model of the heat production of a radio receiver and a functional description of its capacity to receive radio programs should not be regarded as being corresponding models because the described aspects are different. Corresponding models, in contrast, would be a physicalistic and a functional model of the capacity of the radio receiver to receive radio programs, or, if you like, a physicalistic and a functional model of the heat production of a receiver. In terms of structuralism: condition (iii) is met only in such cases in which both corresponding models share the application. We can now give the definition of the correspondence relation (corr):
(corr) Two models of different sort correspond iff
The intersection of the bases of both models is not empty and both are applied to
the same shared element of the respective classes of intended applications.
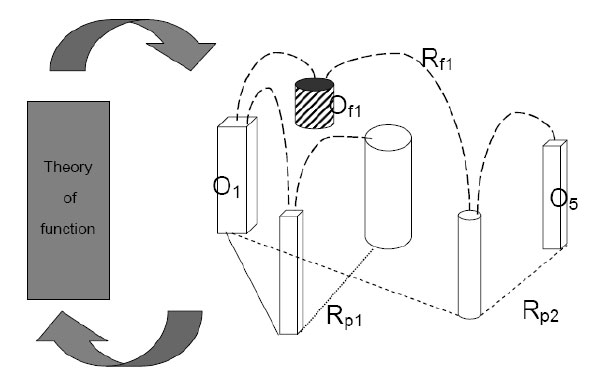
A two-sorted theory element then is a pair of corresponding models. In the simplest case, it is made up of the shared O T2 , plus the classes of physicalistic and of functional relations, R p and R f . This results in a "sandwich-structure" of a two-sorted theory element: Two different slices of bread (the two sets of relations) share the butter (the set of objects):
functional relations: {R f1 , …, R fo }
Objects: {O 1 , …, O n }
physicalistic relations: {R p1 , …, R pm }
] physicalistic model
In the general case, as already mentioned, the classes of objects of both models differ but intersect. In addition, the class I T2 of intended applications has to be specified. I p and I f may be identical. In this case, the class I T2 of intended applications of the two-sorted theory element will be the same as for each of the separate models. The general case is that the two models have slightly different but overlapping intended applications. So, in general, I T2 is the intersection of the classes I p and I f of the classes of intended applications of the two separate models. According to the requirement of (corr), this intersection is never the empty set.
So, the general structure of a two-sorted theory element is:
T 2 = 〈 O p ∪ O f , R p , R f , I p ∩ I f 〉,
with indices "p" and "f" for the physicalistic and functional model, respectively.
Let me point out again that a two-sorted theory element requires that its models differ with respect to their sort. Otherwise they would represent either incompatible or redundant conceptions of the entity in question. In particular, the relations that belong to the different models are of different sort and are not shared among the models. This accounts for the consistency of the theory element, given that the models are themselves consistent: as long as two models share only objects and intended applications, but not relations, no contradictions can occur between them; their combination is consistent. The set of both models will of course contain any inconsistency that might occur within each of the isolated models, but the combination will not give rise to any further inconsistencies.
3. Coherence
My account of correspondence reconstructs how a physicalistic and a functional description of a technical artefact may be used in parallel without competition. In a two-sorted theory element there is, so to say, room for sets of physicalistic relations as well as of functional relations. This shows the consistency of two-model descriptions of technical artefacts. However, this is not yet a satisfying answer to the question of coherence of physicalistic and functional descriptions. It does not spell out the way in which the two models interact.
In the introduction, I have pointed out that this interaction has to be reconstructed in terms of formal relations that hold between the elements of a body of knowledge. The body of knowledge that is in question here is the technical description as reconstructed in terms of a two-sorted theory element. What we are interested in now are the relations that hold between corresponding functional and physicalistic models. These may be of different kind.
First, there might be classical inferential relations, as favoured by BonJour as mediators of coherence ( 1985 ). Due to the multiple realisability of functions and the heterogeneity of the functions that a function bearer may perform (see below, section 5), standard accounts of inference do not seem to be able to explain the coherence of two-sorted theory elements. The same holds true for the most important aspect of the approach of Thagard and co-workers, namely of explanatory and deductive relations ( Thagard et al. 2002 ). Establishing relations of such kind would result in establishing a reduction relation between both sorts of models, which was shown not to hold in the cases considered here (cf. section I). But Thagard exposes another kind of relation that accounts for what he calls coherence by analogy, namely a mapping relation that holds between subsets of a body of knowledge (ibid.). I will concentrate on this mapping relation, which turns out to be a central mediator of coherence in the present case, without ruling out that other relations may hold that further increase coherence of the theory element.
As I have mentioned in my exposition of the notions of structuralism, the core structure of a theory element defines the notions and relations that are available. But not every (if any) scientific theory or technical description is independent of any other theory. Concepts that are defined in other theories can be incorporated by so called intertheoretical links that hold between the two theories ( Balzer et al. 1987 ). Being theoretical terms of other theories, such concepts can be applied in a theory element in question according to the rules that are specified within the theory they originate in. The links are additional constituents of the core structure of a theory element. My claim is that the coherence between a physicalistic and a functional description of a technical artefact is brought about by a concept that is defined in a more general theory and provided by a link: the concept of function.
The link makes the notion of a function available as provided by a theory of function. Different such theories are discussed in the literature, resulting in different accounts of the concept of function. It does not matter for my present purpose which one is preferable, as long as it provides criteria for the functionality of processes or structures as described in a physicalistic way. In principle, this might be an etiological account like Millikan’s ( 1984 ), based on the causal history of an entity, or one based on use plans like that of Houkes and Vermaas ( 2009 ). I have proposed an alternative explication that avoids shortcomings of other theories. It is based on the role that reference to design plays in accounts of the ontogeny or construction of an entity ( Krohs 2004, chs. 4-5; Krohs 2009 ). “Design” includes intentional and natural design, the latter being the outcome of evolutionary processes. My approach therefore integrates biological and technical functions. However, I will not enter the discussion about the adequacy of different theories of function here. For the reconstruction of two-sorted theory elements we merely need a workable concept of function that ascribes functions to components of technical (and biological) systems. Any such concept secures the interaction of physicalistic and functional descriptions.
The role of the theory of function is the following: It provides the notion of function that can be applied to the objects O i and the relations R j of the physicalistic model. Only if elements of R p can be shown to be functional according to the theory of function used, can it be regarded as justified to supplement the physicalistic model with a functional one: the concept of function becomes part of the physicalistic model, but it allows for the addition of a functional one. The theory of function that is applied maps the functional relations R f onto the physicalistic relations R p . This, obviously, need not be a one-to-one mapping. The structures of both models may differ greatly, as long as any relation out of R f can be mapped onto R p as a whole set (Fig. 1).
To sum up, coherence of models in a two-sorted theory element (given the identity of the intended application) is brought about by (i) an – at least partly – shared class of objects and (ii) by the status of some of the physicalistic relations that hold between the objects as being functional according to a link to the theory of function, therefore by a mapping of the functions to physicalistic relations. Such a mapping increases the coherence of a body of knowledge by elucidating, in Thagard’s terminology, an analogy between its different subsets. 6 However, since the mapping imposes relations on the components of the two-sorted theory element, it could in principle introduce not only an account of analogy, but also inconsistencies. This possible source of inconsistencies is not covered by the argument about the structural independence of the pair of corresponding models (section 2), so it is crucial that it is observed by the theory of function. Not giving rise to inconsistencies in the mapping of functions to physicalistic relations might be regarded as a criterion that has to be met by any sound theory of function.
4. Application
I now want to demonstrate the adequacy of my reconstruction using descriptions of the transistor as an example. A transistor is a semiconductor element that was developed as a device for amplification of electric current. From the literature, we can reconstruct a physicalistic model that describes the structure and electric characteristics of the transistor, and a functional model that describes how it works as an amplifier. In the descriptions given in the original U.S. Patents, both models are more or less blurred ( Shockley 1950; Bardeen and Brattain 1950 ). For reconstruction, I therefore refer to the account of the transistor that Darlington gives on the basis of these first patents. In his patent of a transistor pair ( Darlington 1953 ), he gives the following description of the structure of the transistor:
Transistors comprise, in general, a body of semiconductive material and three connections, termed emitter, base and collector, to the body. ... Transistors ... may be classified further as to conductivity type; in an N-type junction transistor, the intermediate zone, i.e., the one with which the emitter and collector zones form junctions, is of N-conductivity type ( Darlington 1953, p. 1).
His description characterises the class of objects the model deals with: Elements of O are a piece of semiconductive material (usually silicon or germanium), atomic impurities, and three connections (made of metal). Free electrons may be added that did not need to be mentioned in the description because they are present in the used material anyway. Next, Darlington describes the physical relations that hold with respect to these objects:
In the utilization of transistors, a number of what may be considered as circuit parameters or aspects are of prime moment. Among and illustrative of such parameters are the current multiplication factor, commonly designated alpha, and the emitter and collector resistances (ibid.).
According to this description, elements of R are the mathematical functions stating the current multiplication factor, and the emitter and collector resistances. In the structuralist reconstruction, the mentioned parameters belong to the class R p of relations of the physicalistic model. In addition, so-called “holes” or defect electrons as defined by the model of semiconductivity ( Wilson 1931 ) will be elements of this class. 7 Darlington further characterises the physicalistic model by describing how the parameters just mentioned are influenced by structural variations:
[The current multiplication factor] is dependent upon a number of controllable factors, such as the width of the intermediate zone … . Similarly, the emitter and collector resistances are amenable to control by design (ibid.).
So, if the required data were provided, the physicalistic model could be stated in a completely quantified way.
What about the functional model? Darlington, like Shockley and Bardeen & Brattain, speaks about amplification of a signal. “Amplification” and “being a signal”, in contrast to the already mentioned physicalistic concepts of a current multiplication factor and of a current, are functional classifications of the transistor’s electric characteristics and of the change or time course of an electric current, respectively. This view is supported by the fact that there is not one single correlate to the signal. It occurs in various realisations, as it may in general be the case with functions. A voltage change of different currents may be the very same signal. Since signal processes are functional, we are dealing with an element of the class R f of functional relations that are part of the functional model.
Since the structure of the transistor as referred to in the functional model does not differ from the description given in the physicalistic model, domain O is identical for both models. (However, only two connections instead of three may be required in some other functional descriptions.) The “sandwich-structure” of the two-sorted theory element is therefore made up of two classes of relations, R p and R f , and a common domain O . Both models, the physicalistic and the functional one, share the intended application Ii, which is the behaviour of the transistor in an electric circuit of a certain type. Therefore, all three requirements for correspondence as posed in section 2 are met: sort difference, identity of the described entity, and identity of the modelled aspect. With respect to the two models, (corr) holds, and the technical description given in the patents has the structure of a two-sorted theory element.
To account for the coherence of a two-sorted theory element, we need to have a look at the mapping of the relations of both models. Above, I have introduced this mapping as a matter of the application of the concept of function. We have seen that the functionalities of amplification and of being a signal are mapped on the physicalistic roles of a current multiplication factor and of fractions of different currents. We do not rely on any particular explication of the concept of function here, so no restriction applies in this regard. It is clear from Darlington’s description that such a mapping holds, mediated by a concept of function that is not further specified. So, coherence by analogy can in fact be found in the transistor example.
5. Accounting for functional ambiguity
We have not yet addressed the fact that the twinning of functional with physicalistic models may be ambiguous. Most technical artefacts can serve different functions, and in general, functions can be realised differently. This is known as heterogeneity of functionality and as multiplicity of realisation, respectively ( Carrier 2000 ). It has to be asked on the one hand, whether the reconstruction presented can account for both, and on the other hand, whether an account of ambiguity brings in any unwanted arbitrariness. Sticking to the example of the transistor, I will first have a look at the heterogeneity of its possible functions. Above, I was concerned with the functional model of the transistor as used as an amplifier. However, it may be used in different ways. Some of these are mentioned in the quoted patents, others not. 8 Most prominent might be the function of the transistor as a switch. The switch model refers to off- and on-states of the transistor. They are characterised by saturation of collector current in the first state, and by zero collector-emitter-voltage in the second state. The characteristic of the transistor in the range in between, which is most important for the amplifier-model of the transistor, almost does not matter for the switch model. Nevertheless, the physicalistic model that corresponds to the functional switch-model is the same one that corresponds to the functional amplification model. Each pair of corresponding models has a common intended application (transistor in electric circuit of a certain type). So we have two different two-sorted theory elements describing the transistor. Functional heterogeneity of technical artefacts (see the two left columns of table 1) can easily be accounted for.
| Function | Artefact | ||
|---|---|---|---|
| Amplification | Transistor | Tube | Multiple realisability of amplification |
| Switching | Transistor | Relay | Multiple realisability ofswitching |
| Functional heterogeneity of transistor use | |||
Multiple realisability of a function can be accounted for in a similar way. Let us regard the function of signal amplification. This function can be realised by a transistor and described by the two-sorted theory element already discussed. Alternatively, it may be realised by a vacuum tube, which was functionally the predecessor of the transistor. Similarly, there are alternative realisations of electrical switches. The switching function may be realised, e.g., by a relay instead of a transistor (see right column of table 1). Let us regard the two realisations of an amplifying element only, a transistor and a tube. Physically, they are completely different. So the physicalistic models are different as well. However, the functional model will differ only with respect to the elements of the domain that refer to the physical entity: to the structure of the vacuum tube and of the transistor, respectively. But the two functional models will define almost the same functional relations over these domains. So again, we have two different two-sorted theory elements, in this case describing two different technical artefacts in similar functional contexts. This accounts for multiple realisability of functions.
At first sight, my approach seems to be fairly liberal with respect to the functions that might be assigned to an artefact. This might be judged as being problematic. Therefore, I want to add some considerations about this issue. I was dealing with descriptions of technical artefacts. Doesn’t this mean that I have to accept any function as relevant for a reconstruction in a two-sorted theory element that anybody likes to describe, no matter whether it has any relation to the actual or intended use of the artefact, the goals that anybody might pursue by using it, or the norms that are set on its construction? First, it seems quite clear that functions of technical artefacts are in fact context dependent in some way. Herbert Simon conceives an artefact as the interface of an internal structure and a (physical) environment. In his view, exactly this interface position seems to bring about the association of a goal with the artefact ( Simon 1996, pp. 6-7). Peter Kroes has adjusted this conception and made clear that the relevant environment is not the physical environment but human action ( Kroes 2002 ). This results in the view of the dual nature of a technical artefact as embedded in a context of human action. My account seems to go another step further and change the environment of human action into an environment of human description. This, I agree, would be a step too far. However, the impression of complete dependency on the description is false. There are two reasons for my claim. (i) I admit that my conception of correspondence allows for a wide range of combinations of physicalistic and functional models. Nevertheless, there is an additional demand for coherence: the theory of function itself has to be applicable in the framework of the physicalistic model. This guarantees that not any effect or relation that can be ascribed to a component of a complex entity may be considered in the functional model, but only functional relations that can be isolated from physicalistic models. So the theory of function has to be specific enough to prevent arbitrary function ascriptions. Reconstruction of theory structure only has to show that the theory of function is crucial in this respect; it does not have to develop this theory. (ii) The validity of the functional part of a two sorted theory element has to be proven by standards as strong as those that are used for the physicalistic part. A functional model that is not in accordance with observations of the structure, dynamics, and possible use of an artefact is not a good model and must not be regarded as a valid functional description. (Such an evaluation would mostly fall within the scope of the special sciences.) But discrimination of good and bad models cannot be a matter of reconstruction. Reconstruction deals with theories only and has no grip on the modelled phenomena. Moreover, it has to be possible to reconstruct even implausible combinations of physicalistic and functional descriptions for the sake of analysis. My claim is only that the reconstruction method has a grip on “mixed” models, not that it, purely as a method, sorts out the best model.
6. Conclusion
Descriptions of technical artefacts consist of physicalistic and functional elements, which can be ascribed to different models. The description as a whole was reconstructed as a two-sorted theory element, which, in the simplest case, combines a pair of corresponding physicalistic and functional models in a sandwich-like structure. This accounts for the consistency of a mixed physicalistic-functional description of a technical artefact. The same theory structure can be found in mixed physicalistic-functional descriptions in biology. It was shown how the concept of function, as provided by an adequate theory of function, maps the relations of the functional model onto relations of the physicalistic one. The mapping relation brings the coherence of a two-sorted theory element about, in terms of what Thagard has dubbed coherence by analogy.
References
Agazzi, E., ed. 1991. The Problem of Reductionism in Science. Dordrecht: Kluwer
Balzer, W., C.U. Moulines and J.D. Sneed. 1987. An Architectonic for Science: The Structuralist Program. Dordrecht: Reidel.
Bardeen, J. and W.H. Brattain. 1950. Three-electrode Circuit Element Utilizing Semiconductive Materials. U.S. Patent No. 2,524,035, Oct. 3, 1950.
Beckermann, A., H. Flohr and J. Kim, eds. 1992. Emergence or Reduction? Essays on the Prospects of Nonreductive Physicalism. Berlin: De Gruyter.
BonJour, L. 1985. The Structure of Empirical Knowledge. Cambridge, MA: Harvard University Press.
Carrier, M. 2000. “Multiplicity and Heterogeneity: On the Relations between Functions and their Realizations,” Studies in the History and Philosophy of Biology and Biomedical Science, 31: 179-191.
Darlington, S. 1953. Semiconductor Signal Translating Device. U.S. Patent No. 2,663,806, Dec. 22, 1953.
Fodor, J. 1974. “Special Sciences (Or: The Disunity of Science as a Working Hypothesis),” Synthese, 28: 97-115.
Houkes, W. and P.E. Vermaas. 2009. “Produced to Use: Combining Two Key Intuitions on the Nature of Artefacts,” Techné, 13 (2): 123-136.
Kroes, P. 2002. “Design Methodology and the Nature of Technical Artefacts,” Design Studies, 32: 287-302.
Kroes, P. 2006. “Coherence of Structural and Functional Descriptions of Technical Artefacts”. Studies in History and Philosophy of Science, 37: 137-151.
Krohs, U. 2004. Eine Theorie biologischer Theorien: Status und Gehalt von Funktionsaussagen und informationstheoretischen Modellen. Berlin: Springer.
Krohs, U. 2008. “Conservative and Non-Conservative Models in Molecular Biology and the Concept of Genetic Information,” presented at the 21st Biennial Meeting of the Philosophy of Science Association, Pittsburgh.
Krohs, U. 2009. “Functions As Based on a Concept of General Design,” Synthese, 166: 69-89.
Krohs, U. (forthcoming). “Dys- mal- et non: l’autre côté de la fonctionnalité,” in: J. Gayon & M. Mossio, eds., Épistémologie de la catégorie de fonction: des sciences de la vie à la technologie. Paris: Presses Universitaires de France.
Millikan, R.G. 1984. Language, Thought and Other Biological Categories: New Foundations for Realism. Cambridge, MA.: MIT Press.
Putnam, H. 1964. “Psychological predicates,” in: W. Capitan and D. Merrill, eds., Art, Mind, and Religion. Pittsburgh: University of Pittsburgh Press: 37-48.
Scheibe, E. 1993. “A new theory of reduction in physics,” in: J. Earman, A.I. Janis, G.J. Massey and N. Rescher, eds., Philosophical Problems of the Internal and External Worlds: Essays on the Philosophy of Adolf Grünbaum. Konstanz: Universitätsverlag Konstanz / Pittsburgh: University of Pittsburgh Press: 249-271.
Shockley, W. 1950. Semiconductor amplifier. U.S. Patent No. 2,502,488, Apr. 4, 1950.
Simon, H.A. 1996. The Sciences of the Artificial. 3 rd edition, Cambridge, MA.: MIT Press (1 st ed. 1969).
Sneed, J.D. 1971. The Logical Structure of Mathematical Physics. Dordrecht: Reidel. 2 nd ed. 1979.
Sober, E. 1999. “The Multiple Realizability Argument against Reductionism,” Philosophy of Science, 66 542-564.
Stegmüller, W. 1986. Theorie und Erfahrung, dritter Teilband: Die Entwicklung des neuen Strukturalismus seit 1973. Berlin: Springer.
Thagard, P., C. Eliasmith, P. Rusnock and C.P. Shelley. 2002. “Knowledge and Coherence,” in: R. Elio, ed., Common Sense, Reasoning, and Rationality, Vol. 11, Oxford: Oxford University Press: 104-131.
van Fraassen, B. 1972. “A Formal Approach to the Philosophy of Science,” in: R.G. Colodny, ed., Paradigms and Paradoxes. The Philosophical Challenge of the Quantum Domain, Pittsburgh: University of Pittsburgh Press: 303-366.
Van Regenmortel, M.H. and D.L. Hull, eds. 2002. Promises and Limits of Reductionism in the Biomedical Sciences. Chichester: Wiley.
Wilson, A.H. 1931. “Theory of Electronic Semi-Conductors,” Proceedings of the Royal Society London, A 133: 458-491.
Endnotes
1 The case of partial reduction is all but an exception. Even for the mentioned standard example for reduction we cannot obtain more than this (Scheibe, op. cit.).
2 For a discussion of reductionism, see, e.g., the contributions in Agazzi (1991), Beckermann et al. (1992), and Van Regenmortel and Hull (2002).
3 For a dissenting view, see Sober (1999).
4 The concept of function has even more normative aspects than the generally acknowledged case of dysfunctionality (Krohs, forthcoming).
5 Specification of some further classes would be required to fully characterise the theory core; only one of them needs to be introduced below.
6 In addition, practical inferences may play an important role, as Peter Kroes has recently pointed out (Kroes 2006).
7 The concepts of Wilson’s model are again provided via a link between his theory and the physicalistic model of the transistor that makes use of it.
8 Bardeen and Brattain (1950, p. 1) generously write about “a novel method of and means for translating electrical variations for such purposes as amplification, wave generation, and the like.”