JITE v40n4 - Problem Representation, Understanding, and Learning Transfer Implications for Technology Education
Problem Representation, Understanding, and Learning Transfer Implications for Technology Education
Mathias J. Sutton
Purdue UniversityTransfer and Problem SolvingProblem solving has received significant attention in the technology education literature over the past two decades, primarily as it relates to curriculum development ( Lewis, Petrina, & Hill, 1998 ). The issue of problem solving emerged as the field grappled with educational goals and related curriculum planning ( Zuga, 1989 ). Hatch (1988) presented guidelines for the teaching of problem solving in technology classrooms. Johnson (1992) proposed a framework that emphasized intellectual processes, mental operations that focus on acquiring new knowledge and applying that knowledge in both familiar and new situations. The calls for including problem solving in technology education curricula helped provide the impetus for a philosophical perspective that merges the positive aspects of behaviorism and those of constructivism.
The emphasis on problem solving in technology education has paralleled the move in general education from behaviorism toward constructivism, or a blend of behaviorism and constructivism. Doolittle and Camp (1999) described how thinking in the early 1900s followed the beliefs of Snedden and Prosser, which were influenced by Thorndike's behaviorist philosophy. In fact, Doolittle and Camp noted that behaviorism was still influential in much of the career and technical education thinking. However, beginning in the mid 1980s, in the technology education and career and technical education literature there have been calls to look toward reform that included conceptual, problem-solving based curricula ( Doolittle & Camp ; National Science Board Commission on Pre-College Education in Mathematics Science and Technology, 1983 ; Westberry, 2003 ).
The calls for reform toward conceptual, problem-based learning were more closely aligned with the constructivist learning theory. The primary tenet of constructivism is that learners actively construct their own knowledge based on their own experiences ( Fosnot, 1996 ). Doolittle and Camp (1999) explained that constructivism is not a unitary theoretical position, but can be thought of as a continuum. They contend that on this continuum, technology education is most closely aligned with cognitive constructivism. Doolittle and Camp further explained that cognitive constructivism emphasizes that knowledge acquisition is an adaptive process and results from active cognizing by individual learners. That is, knowledge (learning) is the result of accurately internalizing and reconstructing some external reality. More specifically, Mayer (1992) summarized that the cognitive constructivist perspective of learning focused on three tenets: (a) the procedures or processes of learning, (b) how learners represent or symbolize knowledge in their mind, and (c) how these representations are organized in the mind of the learner.
Mayer's (1992) tenets provided a starting point for problem-solving research in technology education. Herschbach (1998) acknowledged that the field needed to complete major theoretical and practical work. He explained that there are several examples of research that involved cognitive concepts and instructional design in technology education, but constructivist research implications were yet to be determined.
Lewis, Petrina, and Hill (1998) provided a summary of problem-solving research in technology education over the past two decades. The authors explained that the research was manifest in many forms, from experimentation to instructional design to troubleshooting. Only a few of the technology education research studies have focused on the problem-solving process. Johnson (1989) examined the differences between expert and novice problem solvers on technical troubleshooting problems. McCormick, Murphy, and Hennessy (1994) explored how children constructed knowledge during the design process. Research by Glass (1992) paired technology education students and had them solve problems using the think-aloud technique to help identify students' problem solving processes, their thinking strategies, and their method of solution. The think-aloud technique is a way for researchers to glean what the students are thinking while they are in the midst of problem solving ( Yackel, 1984 ). When instructed to use the think-aloud technique, problem solvers are asked to merely verbalize their thoughts while solving a problem.
These studies, particularly the work of Glass (1992) , helped the field begin to see the specific elements of students' problem-solving processes. Although this is not an exhaustive list of problem-solving research in technology education, it does represent its limited scope and confirms Herschbach's (1998) contention that much theoretical development remains to be completed.
Purpose
The purpose of this article is to examine problem-solving research outside of technology education to help explain the relationship between problem representations, understanding a problem, and learning transfer to new situations. An historical look at the work of cognitive psychologists and mathematics education researchers combined with contemporary perspectives provide the key components of a problem-solving model that may be useful for developing a theoretical framework for future research in the technology education field.
Problem Solving
What is problem solving? There are likely to be as many answers to that question as there are problems. Indeed, what is problematic for one person may not be problematic for another. For the purposes of this article, a problem is a situation in which a person or group is asked to perform a task for which there is no readily accessible algorithm or method which completely determines a solution ( Lester, 1978 ; Yackel, 1984 ). Yackel also differentiated between a problem and an exercise. If an individual already has an accessible algorithm or understands the conceptual structure of the task, then it is an exercise and not a problem.
Jonassen (2003) and Hatch (1988) categorized problems as either well structured or ill structured. Well-structured problems are those that require the application of a finite number of concepts, rules, and principles being studied to a constrained problem situation. Ill-structured problems are more like what is encountered in everyday practice. However, ill-structured problems are typically not well defined or constrained to the topic being studied; and their solutions are not predictable. Meacham and Emont (1989) explained that solving ill-structured problems often requires learners to make judgments and express personal opinions or beliefs about the problem, and as such, are uniquely human interpersonal activities.
No matter how a task is classified, well structured or ill structured, if a person does not have at hand a readily accessible method to solve it, then it is problematic. The problem-solving process necessarily entails creating meaning for oneself, and making mental connections between what is known about the problem and one's existing knowledge and experiences. During this process, Jonassen (2003) claimed it is essential that students learn how to represent the problems they are solving in more than one way. In sum, the problem-solving process involves mentally constructing a problem representation.
Cognitive Psychology and Representation
The main focus of cognitive psychology is to determine how information is stored and accessed in the memories of individuals. The way this information is recorded or expressed is called a representation of that information ( Glass & Holyoak, 1986 ). Glass and Holyoak further distinguished between the content of a representation and the code of a representation. The content of a representation is the information that is to be represented. The code of a representation is the way that information or content is expressed.
To illustrate this representation, consider the concept of money. A crisp dollar bill, a plastic credit card, and a signed traveler's check are examples of the same concept. Each example is physically different than the others. Analogically in each case, there is a different code that represents the same content. A code describes the internal or mental representation of information. Determining the code by which a subject represents information is a primary goal of cognitive psychologists and problem-solving researchers.
Glass, Holyoak, and Santa (1979) made a distinction between two types of code, analog code and analytical code. An analog code has one or both of the following properties. The code represents information that seems continuous, such as the size of common objects (e.g. needles, skyscrapers). The code has properties that are similar to actual perception. For instance, a representation of a dog may be a visual image of the dog. In contrast, analytic codes are codes that consist of associations between representations and what they represent, and rules for constructing new representations. As an illustration, consider the word "chair." The word "chair" is the name given to a piece of furniture, but neither the appearance nor the sound of the word chair bears any resemblance to a real chair. It is, in fact, an arbitrary association. Further, by using the rules of language, we can create a new name for "chair", if we so desire. Other examples of analytic code are systems of mathematics and musical notation.
Yackel (1984) , a mathematics educator, introduced the term "external code" to refer to an expression (written or verbal) of a subject's problem representation. In her investigation, references to external code included the following: diagrams, symbolic notation, equations, and charts or lists. Her subjects were presented with a mathematics-related problem on an individual card. As the subjects solved the problems, she wrote extensive notes of the solver's behavior, including the types of external code.
Problem Representation and Understanding
In 1964 Bobrow (as cited in Paige & Simon, 1966 ) developed a computer program, STUDENT, designed to solve algebra word problems. STUDENT directly translated the words using only syntactic knowledge. The original purpose for writing STUDENT was merely to solve word problems. However, Paige and Simon compared the problem-solving performance of STUDENT to that of human problem solvers. Their intent was to try to describe human behavior while solving algebra word problems. Their results provided evidence that the direct-translation (syntactic) process of STUDENT is a good first approximation in describing human problem-solving performance. Further testing determined that STUDENT could not account for human solution processes that rely on semantic knowledge.
Additional research was prompted by the fact that STUDENT was incapable of semantic translation of algebra word problems. This research led to the development of UNDERSTAND. According to Hayes and Simon (1974) , UNDERSTAND was based on two underlying assumptions. To understand a written problem, the text is read and encoded both semantically and syntactically; and a representation must be made of the newly encoded information. The resulting representation must include what Newell and Simon (1972) defined as a problem space. A problem space consists of the set of problem elements, the initial state of the problem and its goal, an operator or a set of operators for transforming the initial state into the goal, and the restrictions under which the operator may be applied.
It is important to note that UNDERSTAND reads the problem text, then rereads it to semantically and syntactically analyze the structure. Next, this structure is matched against a set of requirements specified as input for the General Problem Solver, a problem-solving program previously developed by Newell and Simon (1972) .
Hayes and Simon (1974) contended that an individual solves a problem using two interactive processes, an understanding process and a solving process. The understanding process generates a problem space from the problem text, and the solving process uses the problem space to search for steps toward solving the problem. The problem-solving episode is assumed to begin with the understanding process and end with the solving process, alternating frequently between the two processes for the duration of the episode. The solving process begins to run as soon as the understanding component generates enough information about the problem space to warrant it. When the solving component runs out of things to do, it calls the understanding component back to generate more specific information for the problem space.
The model that Hayes and Simon (1974) developed addressed several important facets of human problem solving. First, the model explicitly differentiates between the understanding of a problem and the solving of a problem. Even though the solving of a problem follows the understanding, the model shows that these are not sequential stages, but rather, interactive stages.
Transfer of Learning
The effectiveness of education depends, in a large measure, upon the amount and quality of transfer potential of the materials that students learn. Bigge (1976) described transfer of learning as the cornerstone upon which educators should ultimately rest. The International Technology Education Association (2003) described technologically literate people as "problem solvers who consider technological issues from different points of view and relate them to a variety of contexts" (p. 11). This definition implied that technologically literate people are those who are able to transfer their knowledge and learned skills from one situation to another. Hence, the task of technology educators is to provide an environment that promotes the genuine understanding and transfer of learned content.
Transfer and UnderstandingOne research paradigm in the area of transfer focuses on variables affecting problem-solving performance. In research of this type, people are given clues that should aid them when solving problems presented at a later time in the experiment. If transfer occurs, the performance of people who received relevant clues will be superior to that of people who had not received clues. Previous investigations in this area, as noted by Stein, Benningfield, and Hedgecough (1983) , indicated that people do not spontaneously transfer these types of clues to the problem, even though the necessary information is available in memory. In fact, individuals only transferred relevant information when explicitly prompted to do so. In a related study, Reed, Ernst, and Banerji (1974) reported that subjects exhibited positive transfer between similar problems only when they were told of the relationship between the problems and only when they solved the more difficult problem of the pair first. Kulm and Days (1979) studied transfer between problems with related structures. They reported that the solution of related problems appeared to help subjects focus on relevant strategies, but that different problem contexts appeared to interfere with transfer.
The construct of memory has also been the focus of problem-solving research in previous investigations. Krutetskii (1976) has suggested that good and poor problem solvers differ in their recall of information from previously encountered problems. In particular, good problem solvers apparently tended to recall the structural features of a problem, whereas poor problem solvers tended to recall, if anything, the specific details of a problem statement. Additionally, Krutetskii suggested that the difficulty for poor problem solvers might lie in their lack of ability to notice structure, even when it has been presented in the form of a problem's solution. In a similar study, Silver (1979) stated that, "the results relating recall performance and subsequent solution performance on a structurally related problem suggests that significant transfer of information occurred from the target problems to the related problems" (p. 14).
Silver (1979) discovered another relevant finding. He concluded that neither good nor poor problem solvers acknowledged using the information in the target problem to help solve the related problem. He explained that this result was not surprising for the poor solvers, since they tended not to solve either problem. However, one might expect a good solver to access the information from the first problem-solving episode to assist them in the related problem-solving episode. He explained that perhaps the good solvers did not learn how to solve the second as a direct result of the first; that is, they accessed the solution of the related problem independently of the target problem experience.
In a somewhat different study Stein, Benningfield, and Hedgecough (1983) found that the degree of similarity between the clue encoding context and the problem encoding context is an important determiner of transfer. In other words, the degree of prior learning determines the success of a person solving a problem that requires similar knowledge. Richards (1984) concurred, stating that what is remembered seems to be a function of what is originally learned (i.e., facts vs. meaningful concepts), how it is learned (i.e., conceptual perspective), and what cues are given at the time of recall.
Richards (1984) further suggested that many students probably comprehend individual terms or concepts in isolation of each other rather than integrating them within one meaningful structure. This implied that many students have weak organizing schemata, which can actually impede positive transfer. Therefore, if a student learns concepts rather than facts, it would appear that he or she has a relatively organized schema, which will enhance positive transfer. Additionally, if the problem encountered is conceptually similar and structurally similar to the task at hand, then it seems plausible that positive transfer will occur.
Cognitive psychologists have defined understanding in problem solving as the building of a problem representation. Greeno (1977) and Simon and Hayes (1976) suggested that the degree of understanding in problem solving can be determined by a subject's problem representation. At the time of Yackel's (1984) study, the term "understanding" had been used without uniform definition. She, however, developed a list of problem representation characteristics that are indicative of understanding in mathematics problem solving. In addition, Yackel concluded, "the degree of understanding exhibited by a solver in a mathematics problem solving task can be assessed by considering characteristics of the problem representation formed by the solver" (p. 241).
Greeno (1984) investigated the relationship of understanding and mathematical problem solving. Two groups of students were given geometry proof exercises. One group was given problems with alternative knowledge structures that constituted understanding of the relationships in the problem; the other group's problems lacked that understanding. Greeno reported that substantial variation was found among students in their performance on a transfer problem that had the same structure as a set of problems that the students had previously learned to solve. He concluded the schematic knowledge that provided the basis for understanding also provided the basis for transferring problem solving procedures to novel problems.
Jonassen (2003) concurred, noting that to be able to transfer problem-solving skills, students must construct a conceptual understanding of how problems relate to domain (schematic) knowledge; and in doing so, students must learn to represent their understanding in more than one way. These findings are consistent with the view that the ability to transfer knowledge to novel problems provides evidence that students understand the structure that the problems share. Furthermore, the findings indicate that a first step in increasing positive transfer in technology education settings is to determine if the students understand the problem.
The Problem-Solving Triad
The cognitive science and mathematics education literature suggest that the problem-solving process involves several aspects from which three major facets tend to emerge: the solver's representation of the problem, the solver's background experiences, and the solver's understanding of the problem and its structure. A problem representation is how a solver mentally processes or represents the information contained within the problem ( Glass & Holyoak, 1986 ). This representation is directly related to the solver's existing knowledge of the content of the problem. Mathematics education researchers in early number development have provided evidence that some children tend to mentally visualize number words as raised fingers, while other children consider numbers as abstract entities. This suggested that a mental representation depends on an individual's prior knowledge, background experiences, or conceptual schema.
Yackel (1984) explained that when an individual is presented with a problem, he or she encodes the information to form a mental representation of the problem. These associations are established with conceptual knowledge. Different individuals have different conceptual knowledge and will make different associations with their knowledge. In some cases an individual may fail to mentally encode some of the information provided by the problem statement, may establish some relationships different from those intended by the problem statement, or may fail to establish some relationships. Consequently, problem representation is subject dependent. Not only is representation subject dependent, Jonassen (2003) claimed that problem representation is "the key to problem solving" (p. 364).
Together the solver's prior experiences and the representation of the problem work together to establish an understanding of the problem. Yackel (1984) defined understanding a problem as the building of a problem representation. The model in Figure 1 is one depiction of the problem-solving process. The base of the triangle shows the solver's experiences and representation of the problem as the foundation for problem solving. The two work together to establish a complete understanding of the problem to include its underlying structure. The process of understanding is iterative and circular, as depicted by the arrows around the outside. Full understanding of the problem does not usually occur at once. A solver will make mental representations of different aspects of the problem, based on associations with his or her experiences. These associations and representations work jointly to build an understanding. As the problem-solving process continues, the solver builds on already established representations until a complete understanding of the problem exists.
Figure 1 : The Problem-Solving Triad: Key Components in the Problem Solving Process
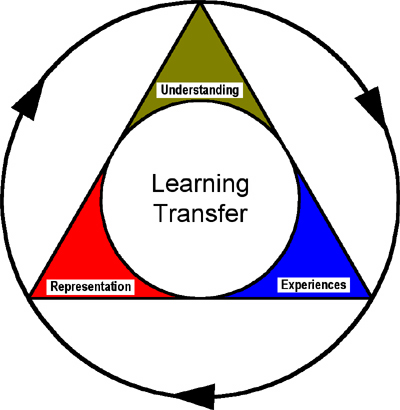
The Hayes and Simon (1974) model of human problem solving differentiated between understanding the problem and solving the problem. They explained that the problem-solving process is nonlinear. Solving may begin without a complete representation of the problem. Yackel (1984) pointed out that the presence of a problem representation in no way implies a problem solution.
The circle at the center of the model represents learning transfer. Once the solver completely understands the problem and its underlying structure, then transfer to similar situations can occur. There is a definite link between the understanding of a problem and transfer of learning. In order to transfer knowledge, it is necessary for students to understand the internal connections between problems and domain knowledge ( Greeno, 1984 ; Jonassen, 2003 ). Learning transfer is at the center of the model because it represents the heart of all learning, applying what has been learned to novel situations.
Implications for Research in Technology Education
Not only does the model in Figure 1 help explain the relationships among representation, background experiences, and understanding in the problem-solving process, but it also provides a focus for problem-solving research in technology education. Given that learning transfer is a central outcome of problem solving, it is natural to explore the relationships between transfer and representation, understanding, and background experiences. In a recent National Science Foundation workshop on establishing a research agenda for transfer of learning, Mestre (2002) summarized the findings of a group of scientists representing diverse fields such as developmental, social, and cognitive psychology; educational media/technology; cognitive science; and research in teaching and learning. The group outlined key themes for future research. One of those themes involved representation, emphasizing the processes, and mechanisms underlying transfer.
Research centered on the relationship of a student's experiences, representations, and understanding in technology needs to be explored by the technology education field. Yackel (1984) explored characteristics of problem representations that tended to indicate a student's understanding of a problem in mathematics education. Although technology education often includes a mathematical problem-solving component, technology problems are usually distinct in that they involve some sort of physical manipulative or artifact. Yackel recommended that the instrument she used to characterize representation in mathematics education be adapted for use in other content areas.
Another problem-solving research idea involves using what Jonassen (2003) described as cognitive tools. Cognitive tools are technologies that "engage and facilitate specific cognitive activities" (p. 372). One genre of cognitive tools includes systems modeling. Model building of real-world systems requires strategic thinking that represents the phenomenon and making connections between its parts. Systems modeling tools enable students to run and test the model and see its output in the form of graphs, tables, or animations. Jonassen stipulated that no empirical research has examined the effects of using system-modeling cognitive tools for representing problems on problem- solving performance. Although Jonassen's work is rooted in cognitive psychology, a model-building approach seems to have great promise for research in the technology education arena.
Although much work has been done over the years in the area of problem solving, much more must be done, especially as it relates to technology education. Mestre (2002) explained that future research needs to build on prior research. Specifically, there is a "need to explore habits of mind that produce better transfer across domains" (p. 14). Furthermore, Mestre's group recognized that such research blends laboratory-based and real-world observations. Technology education provides a fertile field for delving into the underlying processes that affect and enhance problem solving and subsequent transfer.
References
Bigge, M. L. (1976) . Learning theories for teachers (3rd ed.). New York, NY: Harper & Row.
Doolittle, P. E., & Camp, W. G. (1999) . Constructivism: The career and technical education perspective. Journal of Vocational and Technical Education , 16(1), 1-19.
Fosnot, C. T. (1996) . Constructivism: Theory, perspective, and practice . New York, NY: Teachers College Press.
Glass, A. L., & Holyoak, K. J. (1986) . Cognition (2nd ed.). Reading, MA: Addison-Wesley.
Glass, A. L., Holyoak, K. J., & Santa, J. L. (1979) . Cognition . Reading, MA: Addison-Wesley.
Glass, A. R. (1992) . The effects of thinking aloud pair problem solving on technology education students' thinking processes, procedures, and problem solutions . Unpublished doctoral dissertation, University of Minnesota, St Paul, MN.
Greeno, J. G. (1977) . Processes of understanding in problem solving. In N. J. Castellan, D. B. Pisoni, & G. R. Potts (Eds.), Cognitive theory (Vol. 2, pp. 43-48). Hillsdale, NJ: Lawrence Erlbaum Associates.
Greeno, J. G. (1984) . Forms of understanding in mathematical problem solving (No. ED 247 146). Pittsburgh, PA: University of Pittsburgh, Learning Research and Development Center.
Hatch, L. (1988) . Problem solving approach. In W. H. Kemp & A. E. Schwaller (Eds.), Instructional Strategies for Technology Education . Mission Hills, CA: Glencoe.
Hayes, J. R., & Simon, H. A. (1974) . Understanding written problem instructions. In L. W. Gregg (Ed.), Knowledge and cognition . Potomac, MD: Lawrence Erlbaum Associates.
Herschbach, D. R. (1998) . Reconstructing technical instruction. Journal of Industrial Teacher Education , 36(1), 36-61.
International Technology Education Association. (2003) . Advancing excellence in technological literacy: Student assessment, professional development, and program standards . Reston, VA: Author.
Johnson, S. D. (1989) . A description of expert and novice performance differences on technical troubleshooting tasks. Journal of Industrial Teacher Education , 26(3), 19-37.
Johnson, S. D. (1992) . A framework for technology education curricula which emphasizes intellectual processes. Journal of Technology Education , 3(2), 29-40.
Jonassen, D. H. (2003) . Using cognitive tools to represent problems. Journal of Research on Technology in Education , 35(3), 362-381.
Krutetskii, V. A. (1976) . The psychology of mathematical abilities in school children . Chicago, IL: University of Chicago Press.
Kulm, G., & Days, H. (1979) . Information transfer in solving problems. Journal for Research in Mathematics Education , 10(2), 94-102.
Lester, F. K. J. (1978) . Mathematical problem solving in the elementary school: Some educational and psychological considerations. In L. L. Hatfield & D. A. Bradbard (Eds.), Mathematical problem solving: Papers from a research workshop . Columbus, OH: ERIC/SMEAC. (ERIC Document Reproduction Service No. ED156446).
Lewis, T., Petrina, S., & Hill, A. M. (1998) . Problem posing - Adding a creative increment to technological problem solving. Journal of Industrial Teacher Education , 36(1), 5-35.
Mayer, R. E. (1992) . Learners as information processors: Legacies and limitations of educational psychology's second metaphor. Educational Psychologist , 31(3/4), 151-161.
McCormick, R., Murphy, P., & Hennessy, S. (1994) . Problem-solving processes in technology education: A pilot study. International Journal of Technology and Design Education , 4(1), 5-34.
Meacham, J. A., & Emont, N. M. (1989) . The interpersonal basis of everyday problem solving. In J. D. Sinnott (Ed.), Everyday problem solving: Theory and applications . New York, NY: Praeger.
Mestre, J. (2002) . Transfer of learning: Issues and research agenda (No. NSF03-212). Arlington, VA: National Science Foundation.
National Science Board Commission on Pre-College Education in Mathematics Science and Technology. (1983) . Educating Americans for the 21st century . Washington, DC: Author.
Newell, A., & Simon, H. A. (1972) . Human problem solving . Englewood Cliffs, NJ: Prentice Hall.
Paige, J. M., & Simon, H. A. (1966) . Cognitive processes in solving algebra word problems. In B. Kleinmuntz (Ed.), Problem solving: Research, method, and theory (pp. 51-119). New York, NY: Wiley.
Reed, S. K., Ernst, G. W., & Banerji, R. (1974) . The role of analogy in transfer between similar problem states. Cognitive Psychology , 6, 436-450.
Richards, B. (1984, January) . Availability of prior knowledge and its effect on transfer of learning . Paper presented at the meeting of the Association for Educational Communication and Technology, Dallas, TX.
Silver, E. A. (1979, April) . Problem-solving performance and memory for mathematical problems: Solving related problems . Paper presented at the meeting of the American Educational Research Association, San Francisco, CA.
Simon, H. A., & Hayes, J. R. (1976) . The understanding process: Problem isomorphs. Cognitive Psychology , 8, 165-190.
Stein, B. S., Benningfield, S., & Hedgecough, C. A. (1983, March) . Constraints on the automaticity of transfer on problem solving . Paper presented at the meeting of the Southeastern Psychological Association, Atlanta, GA.
Westberry, R. (2003) . Design and problem solving in technology education. In K. R. Helgeson & A. E. Schwaller (Eds.), Selecting instructional strategies for technology education . Peoria, IL: McGraw-Hill Glencoe.
Yackel, E. B. (1984) . Characteristics of problem representation indicative of understanding in mathematics problem solving . Unpublished doctoral dissertation, Purdue University, West Lafayette, IN.
Zuga, K. F. (1989) . Relating technology education goals to curriculum planning. Journal of Technology Education , 1(1), 34-58.
Sutton is Assistant Professor in the Department of Industrial Technology at Purdue University in West Lafayette, Indiana. Sutton can be reached at mjsutton@tech.purdue.edu .