JOTS v39n1 - Reducing the Bullwhip Effect in the Supply Chain: A Study of Different Ordering Strategies
Reducing the Bullwhip Effect in the Supply Chain: A Study of Different Ordering Strategies
M. Affan Badar, Shyamsundarreddy Sammidi, and Leslie Gardner
Abstract
Profitability of a company can be affected by the costs associated with backlogs and large inventories due to the bullwhip effect in the supply chain. This work aims to find an ordering strategy that is practical and can minimize the bullwhip effect. Five strategies with different levels of information about inventory and components along the supply line have been compared with the just in time (JIT) pull strategy and the usage of point of sale (POS) data. This work uses the beer game spreadsheet simulation developed by Adams, Flatto, and Gardner (2008) . The simulation shows material and information flow in a four-echelon supply chain. Expressions for cost incurred and profit obtained by each player (manufacturer, distributor, wholesaler, and retailer) have been developed. Graphs for cost and profit with time are plotted. The strategy using POS data is found to be the best, and the pull strategy to be the next best. However, both require discipline. This study shows that putting information about the inventory levels and components of the supply line into an ordering strategy can also minimize the bullwhip effect.
Keywords: Supply chain, bullwhip effect, ordering strategy, beer game, inventory
Introduction
A supply chain integrates, coordinates, and controls the movement of goods and materials from a supplier to a customer to the final consumer, which therefore involves activities like buying, making, moving, and selling ( Emmett, 2005 ). Fast-rising supply chain risks are poorly understood and managed by most companies, according to the World Economic Forum ( Ladbury, 2008 ). Profit is the main goal of any commercial organization. To obtain profit one should reduce the costs incurred by manufacturing the product economically and reduce the supply chain costs. Supply chain costs involve inventory costs, which have a considerable share in determining the cost of the product. As the economy changes, as competition becomes more global, it is no longer company versus company, but it is supply chain versus supply chain ( Henkoff, 1994 ).
Customer order plays a vital role in the supply chain; it actually triggers all the supply chain activities. Supply chain activities begin with a customer order and end when a satisfied customer has paid for the purchase ( Chopra & Meindl, 2004 ). It should be noted that information flows in the supply chain are also as important as material flows. The whole supply chain process is kept moving by information flow from retailer to wholesaler, wholesaler to distributor, and distributor to manufacturer. Effective supply chain management maintains satisfied customers, growth in company market share, constant revenue growth, capability to fund continuous innovation, and capital investment for more value.
According to Simchi-Levi, Kaminsky and Simchi-Levi (2007) effective supply chain management reduces the costs incurred and thus increases the profit. It is very important to analyze demand and order in such a way that it reduces the costs incurred. Lead time is a critical component in making inventory decisions. Information delays are also one of the main components of total lead time, so electronic data interchange may reduce the delays and offer benefits through reduction in both the size and variability of orders placed ( Torres & Moran, 2006 ).
Despite the undoubted benefits of the lean manufacturing and supply chain revolutions, supply chain instability still continues (often described as bullwhip effect), which harms firms, consumers, and the economy through excessive inventories and poor customer service ( Torres & Moran, 2006 ). The bullwhip effect refers to the phenomenon where demand variability amplifies as one moves upstream in a supply chain, from consumption to supply points (from retailer to manufacturer) ( Lee, Padmanabhan, & Whang, 1997a ). It is an important demand and supply coordination problem that affects numerous organizations, and it is a major phenomenon in the beer game model ( Kumar, Chandra, & a,p; Seppanen, 2007 ). Because of the bullwhip effect, the variability increases at each level of a supply chain as one move from customer sales to production ( Chen, Drezner, Ryan, & Simchi-Levi, 2000 ). Lee et al. (1997a) lists demand signal processing, order batching, price fluctuations, and shortage gaming as the causes for bullwhip effect. Bhattacharya and Bandyopadhyay (2011) presented a good review of the causes of bullwhip effect. According to Chen (1999) a simple forecast formula, such as exponential smoothing or a simple moving average method can lead to bullwhip behavior in certain supply chain settings.
This work is focused toward supply chain costs by minimizing the bullwhip effect. A variety of remedies for the bullwhip effect have been proposed. For the beer game, Sterman (1989) modeled the ordering behavior of players in terms of an anchoring and adjustment heuristic. He used simulation to calculate the parameters that give the minimum total costs for the game. The beer game was developed by Sloan’s System Dynamics Group in the early 1960s at MIT. It has been played all over the world by thousands of people ranging from high school students to chief executive officers and government officials ( Sterman, 1992 ). Although this model is useful for simulation studies and development of theory, it probably has limited application for “real world” practitioners looking for effective decision rules. Industry experts and analysts have cited two recent innovations: the Internet and radio frequency identification (RFID), which t can improve supply chain performance by dampening the bull-whip effect ( Lee, Padmanabhan, & Whang, 2004 ).
One of the most popular remedies is complete visibility of POS order data throughout the supply chain. However, Croson and Donohue (2003) conducted an experiment to evaluate whether humans actually use POS data in the beer game when such data was available. Interestingly they found that humans were still inclined to over order, although not as much as when POS data was not available. Thus, disciplined human behavior is required as well as visible information. Another potential remedy is the pull system of JIT manufacturing. Reducing variability in all aspects of a manufacturing system is one of the principles of JIT and lean manufacturing for eliminating waste and cost. JIT utilizes a pull system in which material is produced only when requested and moved to where it is needed. JIT partnerships throughout a supply chain occur when suppliers and purchasers work together to remove waste, drive down costs, and extend JIT to the supply chain ( Heizer & Render, 2001 ). This can involve information sharing of forecasts as in point of sale (POS) strategies or can involve extending the pull system to the supply chain.
This study uses simulations developed in Microsoft Excel by Adams et al. (2008) to assess the impact of using simple adjustment heuristics based on information about inventory levels (inventory less backlog), orders in mail delays, materials in shipping delays, and the immediately upstream supplier’s backlog to remedy the demand forecast updating the cause of the bullwhip effect in a four-echelon supply chain as represented by the beer game. The objective is to determine if providing all information about inventory levels and components along the supply line into an ordering strategy is superior to the JIT pull strategy and the use of POS data. Equations for cost and profit obtained by each player in the supply chain (manufacturer, distributor, wholesaler, and retailer) have been determined. The study assumes that the manufacturer satisfies the distributor’s order and replenishes from limitless supply of raw material, while the distributor supplies the products to wholesaler, who in turn satisfies the demand of the retailer. The customer orders are placed with the retailer.
Background
Lee et al. (2004) mentioned that Forrester was the first person who documented the phenomenon of bullwhip effect, but the term was not coined by him. As per O’Donnell, Maguire, McIvor and Humphreys (2006) , Forrester studied the dynamic behavior of simple linear supply chains and presented a practical demonstration of how various types of business policy create disturbance, and he stated that random meaningless sales fluctuations could be converted by the system into annual or seasonal production cycles.
The term “bullwhip effect” was coined by Procter & Gamble when researchers studied the demand fluctuations for Pampers. If there is no proper channel of information passage between the players in a supply chain (retailers, wholesalers, distributors and manufacturers), this leads to inefficiency like excessive inventories, quality problems, higher raw material costs, overtime expenses, and shipping costs ( Lee et al. 1997a , b ; Chen et al. 2000 ). According to Cao and Siau (1999) a change in demand is amplified as it passes between members in the supply chain.
Classic management techniques are widely employed to reduce the bullwhip effect in supply chains. In the JIT system, materials are moved when required, and the suppliers and purchasers work together to eliminate waste reducing the cost of production ( Heizer & Render, 2001 ). Croson and Donohue (2003) examined the impact that POS data sharing had on ordering decisions in a multi-echelon supply chain. In a web-based simulation for supply chain management employing electronic data interchange similar to POS data, Machuca and Barajas (2004) found significant reductions in the bullwhip effect and supply chain inventory costs. Vendor- managed inventory (VMI) is another excellent method for reducing the bullwhip effect, and it has been employed by many international companies, such as Procter & Gamble and Wal-Mart, but the problem associated with this method is the sharing of information between retailer and factory ( Lee et al. 1997a , b ).
Warburton, Hodgson and Kim (2004) developed equations to compute the order and demand to nullify the bullwhip effect using a generalized order-up-to (OUT) policy. Control theory is another popular approach to reduce the bullwhip effect. Lin, Wong, Jang, Shieh, and Chu (2004) applied z-transforms to reduce the bullwhip effect, whereas Dejonckheere, Disney, Lambrecht, and Towill (2003) examined the bullwhip effect by using transfer function analysis. Many other researchers used computational intelligence techniques such as fuzzy logic, artificial neural networks, and genetic algorithms to reduce the bullwhip effect ( O’Donnell et al. 2006 ). Carlsson and Fuller (2001) employed fuzzy logic. Goldberg (1989) , Vonk, Jain, and Johnson (1997) and Moore and DeMaagd (2005) used genetic algorithms. Sarode and Khodke (2009) developed a multi-attribute decision-making technique: analytic hierarchy process (AHP).
A correct measurement is an essential start to investigating problems caused by demand amplification and to assess which measures can be taken to reduce this amplification. Fransoo and Wouters (2000) explained three issues in measuring the bullwhip effect: first, the sequence of aggregation of demand data, second filtering out the various causes of the bullwhip effect, and last the inconsistency in demand. Operational researchers also have worked on finding ways to reduce the bullwhip effect. For instance, Adelson (1966) studied simple supply chain systems, but the methodology required complex mathematics for solving the problem ( Towill, Zhou, & Disney, 2007 ).
Simulation also has been used in supply chain management to study the bullwhip effect. The beer game is a hands-on simulation that demonstrates material and information flows in a supply chain. As mentioned previously, it was developed by the Systems Dynamic Group of Sloan school of Management at the Massachusetts Institute of Technology. Using the beer game, Sterman (1989) demonstrated that the players systematically misinterpret feedback and nonlinearities, and underestimate the delays between action and response, which leads to bad decision making and causes problems in the behavior of the supply chain ( Torres & Moran, 2006 ). Jacobs’ (2000) Internet version of the beer game is brief in description and is limited solely to its characteristics and how that game is played. Machuca and Barajas’ (2004) web-based simulation using an electronic data interchange resulted in significant reductions in the bullwhip effect and supply chain inventory costs. Moyaux and McBurney (2006) used some kinds of speculators in agent-based simulations and concluded that these speculators can decrease the price fluctuations caused by the bullwhip effect. However, these speculators are not cost efficient and price bubbles may occur, particularly if too many speculators are used.
In their study, Kaminsky and Simchi-Levi (1998) showed the bullwhip effect, and they explained the effect of passing from a decentralized structure to a centralized structure and also observed the effects of shortening the lead time. Steckel, Gupta, and Banerji (2004) examined how changes in order and delivery cycles, shared POS data, and patterns of consumer demand affected the dynamics in a channel and thereby the severity of the bullwhip effect.
Cangelose and Dill (1965) considered the problem of the bullwhip effect from an organizational learning perspective. Jung, Ahn, Ahn, and Rhee (1999) analyzed the impacts of buyers’ order batching had on the supplier demand correlation and capacity utilization in a simple branching supply chain involving two buyers whose demands are correlated; they found that increase in the size of the order lot mitigates the correlation of purchase orders. Cachon & Lariviere (1999) investigated the performance of balanced ordering policies in a supply chain model with multiple retailers and summarized that the bullwhip effect would depend on the order cycle and batch size. They recommended balanced ordering with small batch size and a long order interval to reduce the suppliers’ demand variance.
This section has summarized a review of literature on the bullwhip effect. Researchers have employed JIT and POS data, mathematical techniques, algorithms, simulation, and balancing of order and delivery cycles in order to reduce the bullwhip effect.
The Beer Game
The beer game is played as a board game with four players: a retailer, a wholesaler, a distributor, and a factory ( Adams et al., 2008 ). Customer orders are placed with the retailer who fills them to the extent possible. The retailer then orders from the wholesaler to replenish his/her stock. Similarly the wholesaler fills retailer orders and replenishes from the distributor who in turn fills wholesaler orders and replenishes from the factory. The factory fills distributor orders and replenishes from a limitless supply of raw material. All players keep records of backlogs, or unfilled orders, and attempt to fill them as soon as possible. Shipping delays of two weeks (or periods) separate each player, as do information delays of two periods. Initially, all four players have twelve units of inventory, and four units of inventory are on each square representing a shipping delay. Similarly, all of the orders in the information pipeline at the start of the game are for four units. The game board is shown in Figure 1.
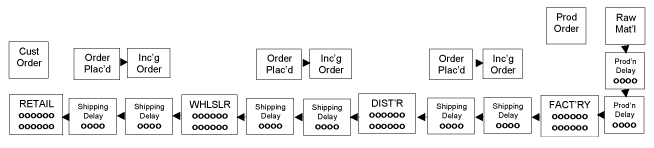
The objective of the game is to fill all customer orders without carrying excessive inventories or having excessive backlogs. The players must fill backlogs eventually. For the first several periods of the game, the customer orders are at four units each period. At some point, the customer orders jump to eight units and remain at that level for the rest of the game. The only stochastic part of the beer game is the human behavior in placing orders but human behavior rarely fails to produce the bullwhip effect. The game runs for 50 periods or until the players become frustrated with excessive backlogs and inventories and the point about the bullwhip effect has been made.
Methodology
The objective of this work is to find whether using information about inventory levels and components of the supply line into an ordering strategy is superior to the JIT pull strategy and the use of POS data at all levels of supply chain. To explore this, cost incurred and profit obtained by each member in a four-echelon supply chain (manufacturer, distributor, wholesaler, and retailer) are computed. For finding the costs incurred and profit obtained, data from spreadsheet beer game simulation developed by Adams et al. (2008) is used. After calculating costs and profit for each player of the supply chain, graphs are plotted between cost versus week (period) and profit versus week for seven different ordering strategies. These graphs have also been plotted for different lead times by Sammidi (2008) ; however, this paper uses the lead time of two periods.
Sterman (1989) developed an expression for ordering behavior in the beer game in terms of adjustment heuristic that is,
I0 t = L̂ t + AS t + ASL t
Where:
・ I0 t - Order rate in time period t,
・ L̂ t - expected demand in period t,
・ AS t - Difference between the desired stock and actual stock in period t, and
・ ASL t - Difference between the desired and actual supply line in time period t.
The anchoring heuristic L̂ t is often determined using exponential smoothing as follows:
L̂ t = θL t-1 + (1- θ )L̂ t-1
Where L t-1 is the demand for the previous period, L̂ t-1 is the forecast value of demand for previous period, θ is a parameter varying between 0 and 1.
The adjustment for stock AS t is the difference between the desired stock S* and the actual stock S t multiplied by a parameter α s (0 ≤ α s ≤ 1) specifying the fraction of the difference ordered each period.
AS t = α s ( S* - S t )
The adjustment for supply line is the difference between desired supply line SL* and the actual supply line multiplied by a parameter α SL specifying the fraction of the difference ordered each period.
ASL t = α SL ( SL* t - SL t )
The supply line consists of orders in mail delays, the immediately upstream supplier’s backlog, and the material in shipping delays ( Adams et al., 2008 ). We can have for orders: 0 ≤ α SLO ≤ 1; for material: 0 ≤ α SLM ≤ 1; and for upstream backlog 0 ≤ α SLB ≤ 1.
The cost incurred by each member is calculated by finding the various costs involved. The cost includes the price of the product, ordering cost, holding costs or inventory cost, and the backlog cost. The backlog cost is the cost, which the supplier must pay as a penalty if he/she cannot deliver the product within the time actually agreed upon. The backlog cost per item is computed by assuming it to be double the cost of the inventory per item ( Nienhaus, Zeigenbein, & Schoensleben, 2006 ). Thus,
Total cost = (Cost per item*number of items ordered) + Ordering cost + Inventory cost (2*Inventory cost per item*number of backlog items)
The ordering cost per order and inventory cost per item are assumed to be $100 and $0.5, respectively for each member in the four-echelon supply chain. Hence,
Total cost = Price per item*number of items ordered + 100 + 0.5*number of items in Inventory + 2*0.5* number of backlog items.
The value of price per item increases from manufacturer to retailer. The price per item for the manufacturer is assumed to be $10, and then it is increased by 2.5 times $10 when it comes to the distributor and then 2.5 times the price of the distributor for the wholesaler and then again 2.5 times the price of the wholesaler for the retailer. Thus, the price per item for distributor is $25, for wholesaler it is $62.5 and for the retailer it is $156.25. The number of items ordered, the number of items in inventory, and the backlogs values have been taken from the simulation developed by Adams et al. (2008) . After finding the total cost incurred for each member, the revenue of each member of the supply chain is calculated. The revenue for the manufacturer is the price that the distributor pays for the product; the revenue for the distributor is the price that the wholesaler pays for the product; and the revenue for the wholesaler is the price that the retailer pays for the product.
Profit of each member is calculated by deducting their cost incurred from their revenue obtained, and graphs are developed for seven different cases. Sammidi (2008) contains the detailed work. The seven cases are shown in Table 1.
| Case | L̂ t | AS t | ASL t |
|---|---|---|---|
| 1 | θ = 1, (Pull) | α s = 1, (12 – (inv – bklg)) | None |
| 2 | Pull | 12 – (inv – bklg) | α SLO = 1, α SLM = 0, α SLB = 0, (Less orders) |
| 3 | Pull | 12 – (inv – bklg) | α SLO = 0, α SLM = 1, α SLB = 0, (Less material) |
| 4 | Pull | 12 – (inv – bklg) | α SLO = 1, α SLM = 1, α SLB = 0, (Less material and orders) |
| 5 | Pull | 12 – (inv – bklg) | α SLO = 1, α SLM = 1, α SLB = 1, (Less material, orders, and upstream supplier’s backlog) |
| 6 | Pull | α s = 0, None | None |
| 7 | POS | Not applicable | Not applicable |
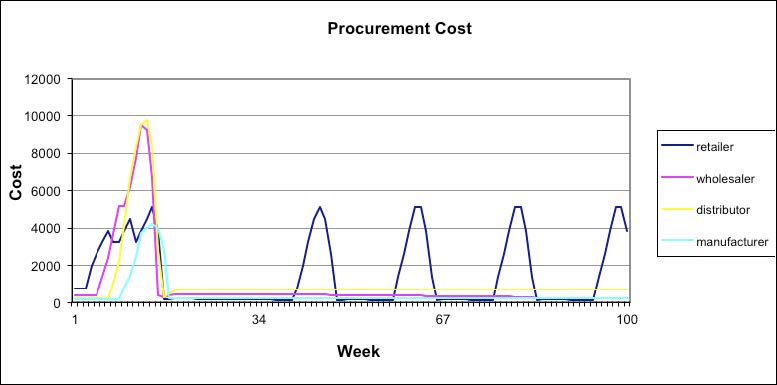
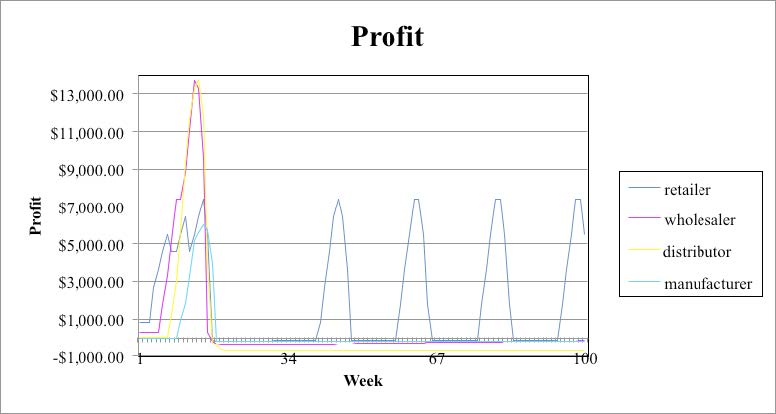
Among the seven cases mentioned, the first five cases demonstrate the reduction in bullwhip effect as more and more information is interpreted into the supply line. The first case uses an anchoring heuristic of ordering what was ordered, which is equivalent to the pull system, but with a stock adjustment of the full difference between the ideal stock of 12 and the inventory level, that is, 12 – (inventory – backlog). This case displays the largest bullwhip effect as shown in Figures 2-3 of all cases studied. Cases 2 – 5 use the same anchoring and stock adjustment heuristics of Case 1, but they have supply line adjustment heuristics that compensate for more and more of the supply line (orders in mail delays, material in shipping delays, and immediate upstream supplier’s backlog). As more and more of the supply line is compensated, the bullwhip effect diminishes in Cases 2 – 4 until it is completely eliminated in Case 5, when the entire supply line consisting of the sum of the orders in mail delays, the immediate upstream supplier’s backlog, and the material in shipping delays is accounted for.
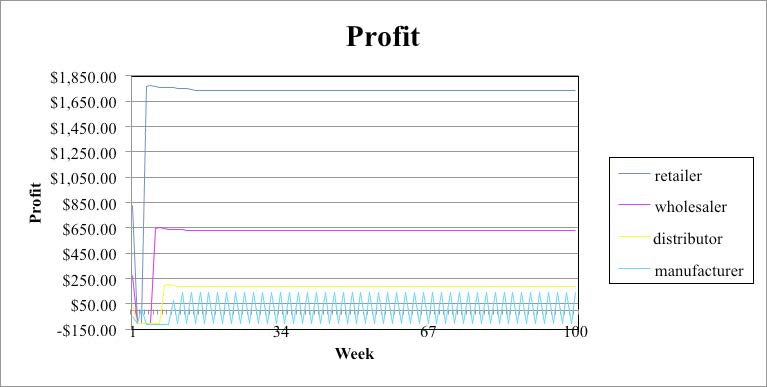
This paper shows graphs in Figures 2 – 6 for cost and profit versus period (week) for four cases with lead time of two periods. Because profit is revenue minus cost, the profit graph takes into consideration the effect on cost. Hence, there is no need to display the cost versus week graph for each of the cases. Cost and profit for Case 1 are displayed in Figures 2 and 3. Case 1 illustrates the maximum bullwhip effect when no supply chain line information is provided. Case 5 (Figure 4), Case 6 (Figure 5), and Case 7 (Figure 6) show that the bullwhip effect is eliminated. In Case 5, adjustments for supply chain in terms of order delay, material in shipping delay, and upstream backlog have been taken into account. Case 6 is pull strategy, which does not adjust for either stock or supply line. It does not show any bullwhip but produces a steady-state error. This error is better than the bullwhip effect. Also the steady error of Case 6 is slightly better than that of Case 5. In Case 7 there is complete exchange of data between the members of the supply chain, which eliminates the bullwhip effect. However, Case 6 and Case 7 both require discipline and at times are not easy for companies to follow.
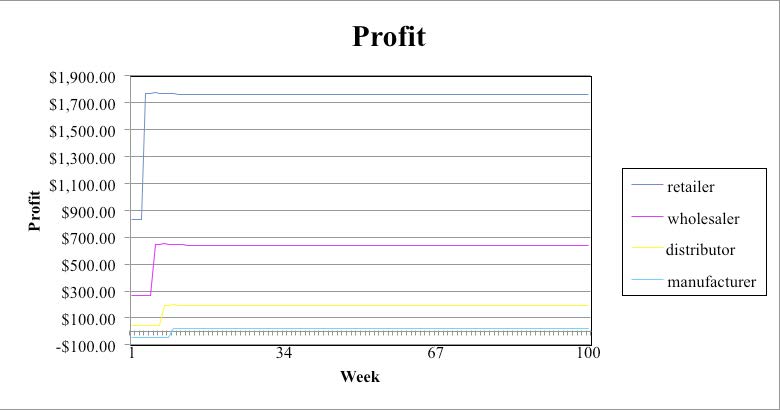
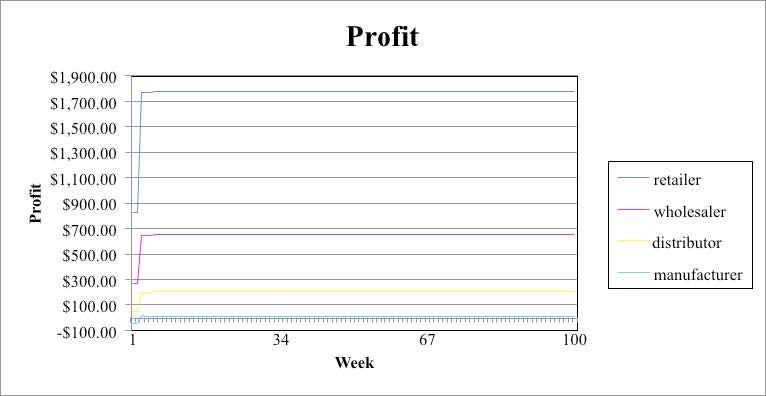
Conclusion
This study is an extension of the work done by Adams et al. (2008) , and it uses the beer game spread sheet simulation developed by them. The beer game ( Sterman, 1992 ), shows information and material flow in a four-echelon supply chain. An attempt has been made in the current work to find an ordering strategy that is easy to employ and can minimize the bullwhip effect. Five strategies (Case 1 through Case 5) with different levels of information about inventory and components along the supply line have been compared with the JIT pull strategy (Case 6) and the usage of POS data (Case 7). The cost incurred and profit obtained by each player (manufacturer, distributor, wholesaler, and retailer) of the supply chain for the seven ordering strategies have been determined. Graphs for cost and profit versus time have been plotted.
From the graphs it is evident that as more and more information is provided for the inventory and components along the supply line from Case 1 through Case 5, the bullwhip effect is reduced. Case 1 uses an anchoring heuristic of ordering what was ordered and a stock adjustment to compensate for the difference between the ideal stock and the inventory level. This case shows the largest bullwhip effect. Cases 2 – 5 use the same anchoring and stock adjustment heuristics of Case 1, but have supply line adjustment heuristics that compensate for more and more of the supply line. As more and more of the supply line is compensated, the bullwhip effect diminishes in Cases 2 – 4 until it is completely eliminated in Case 5, when the entire supply line consisting of the sum of the orders in mail delays, the immediate upstream supplier’s backlog, and the material in shipping delays is accounted for.
Case 6 is a pull strategy, which does not adjust for either stock or supply line. It does not show any bullwhip, but it produces a steady-state error. This error is better than the bullwhip effect. Also the steady error of Case 6 is slightly better than that of Case 5. In Case 7 there is complete exchange of data between the members of the supply chain, which eliminates the bullwhip effect. Thus, Case 7 where POS data is used is the best strategy that eliminates the bullwhip effect and Case 6 (pull strategy) is the next best. However, Case 6 and Case 7 both require discipline and at times are not easy for companies to follow. POS has an additional issue because of the reluctance between each member of the supply chain to share information. In such circumstances, Case 5 is a reasonable strategy with better applicability.
Dr. M. Affan Badar is the Chair of the Department of Applied Engineering & Technology Management at Indiana State University, Terre Haute. He is a member of Mu Chapter of Epsilon Pi Tau.
Shyamsundarreddy Sammidi graduated with a Masters in Industrial Technology in 2008 from Indiana State University, Terre Haute, and joined ISU’s MBA program.
Dr. Leslie Gardner is a Professor of Mathematics and Operations Management at the University of Indianapolis.
References
Adams, J., Flatto, J., & Gardner, L. (2008). Analyzing supply chain performance using beer game. In K. E. Stecke (Ed.), Operations management education review: Vol. 2 (pp. 41-68). Scotland, UK: Neilson Journals Publishing.
Adelson, R. M. (1966). The dynamic behavior of linear forecasting and scheduling rules. OR Quarterly, 17 (4), 447-462.
Bhattacharya, R., & Bandyopadhyay, S. (2011). A review of the causes of bullwhip effect in a supply chain. The International Journal of Advanced Manufacturing Technology, 54 (9-12), 1245-1261.
Cachon, G. P., & Lariviere, M. A. (1999). Capacity choice and allocation: Strategic behaviour and supply chain performance. Management Science, 45 (8), 1091-1108.
Cangelose, V. E., & Dill, W. R. (1965). Organizations learning: Observations toward a theory. Administrative Science Quarterly, 10 , 175-203.
Cao, Q., & Siau, K. (1999). Artificial intelligence approach to analyzing the bullwhip effect in supply chains. Proceedings of the 5th Americas Conference on Information Systems (pp. 44-45). Milwaukee: AMCIS.
Carlsson, C., & Fuller, R. (2001). Reducing the bullwhip effect by means of intelligent, soft computing methods. P roceedings of the 34th Annual Hawaii International Conference on System Sciences. 3-6 Jan 2001, p. 3027. IEEE Computer society.
Chen, F. (1999). Decentralized supply chains subject to information delays. Management Science, 45 (8), 1016-1090.
Chen, F., Drezner, Z., Ryan, J. K., & Simchi-Levi, D. (2000). Quantifying the bullwhip effect: The Impact of forecasting, lead times, and information. Management Science, 46 (3), 436-443.
Chopra, S., & Meindl, P. (2004). Supply chain management: Strategy, planning and operation. Englewood Cliffs, NJ: Prentice Hall.
Croson, R., & Donohue, K. (2003). Impact of POS data sharing on supply chain management: An experimental study. Production and Operations Management, 13 (4), 340-353.
Dejonckheere, J., Disney, S. M., Lambrecht, M. R., & Towill, D. R. (2003). Measuring and avoiding the bullwhip effect: A control theoretic approach. European Journal of Operational Research, 147 (3), 567-590.
Emmett, S. (2005). Excellence in Warehouse Management: How to Minimize Costs and Maximise Value. Hoboken, NJ: John Wiley & Sons.
Fransoo, J. C., & Wouters, M. J. (2000). Measuring the bullwhip effect in the supply chain. Supply Chain Management: An International Journal, 5 (2), 78-79.
Goldberg, D. E. (1989). Genetic algorithms in search, optimization and machine learning. Boston, MA: Addison-Wesley.
Heizer, J. H., & Render, B. (2001). Operations management (6th ed.). Upper Saddle River, NJ: Prentice Hall.
Henkoff, R. (1994). Delivering the goods. Fortune, 130 (11), 34-47.
Jacobs, F. R. (2000). Playing the beer distribution game over the internet. Production and Operations Management, 9 (1), 31-39.
Jung, H. D., Ahn, H. S., Ahn, B. H., & Rhee, S. K. (1999). Impacts of buyers’ order batching on the supplier’s demand correlation and capacity utilization in a branching supply chain. Production Planning and Control, 10 (5), 472-485.
Kaminsky, P., & Simchi-Levi, D. (1998). A New-computerized Beer game: A tool for teaching the value of integrated supply chain management. In H. Lee & S. M. Ng (Eds.) Supply chain and technology management (pp. 216-225). Miami, FL: POMS.
Kumar, S., Chandra, C., & Seppanen, M. S. (2007). Demonstrating supply chain parameter optimization through beer game simulation. Information Knowledge Systems Management, 6 (4), 291-322.
Ladbury, A. (2008). Supply-chain risks misunderstood, mismanaged: Report. Business Insurance, 42 (2), 23.
Lee, H. L., Padmanabhan, V., & Whang, S. (2004). Comments on “information distortion in a supply chain: The bullwhip effect.” Management Science, 50 (12), 1887-1893.
Lee, H. L., Padmanabhan, V., & Whang, S. (1997a). The bullwhip effect in supply chains. Sloan Management Review, 38 (3), 93-102.
Lee, H.L., Padmanabhan, V., & Whang, S. (1997b). Information distortion in a supply chain: The bullwhip effect. Management Science, 43 (4), 546-558.
Lin, P. H., Wong, D. S. H., Jang, S. S., Shieh, S. S., & Chu, J. Z. (2004). Controller design and reduction of bullwhip for a model supply chain system using z-transform analysis. Journal of Process Control, 14 (5), 487-499.
Machuca, J.A.D., & Barajas, R. P. (2004). The impact of electronic data interchange on reducing bullwhip effect and supply chain inventory costs. Transportation Research Part E: Logistics and Transportation Review, 40 (3), 209-228.
Moore, S. A., & DeMaagd, K. (2005). Using a genetic program to search for supply chain reordering policies. In U-M. O’Reilly, T. Yu, R. Riolo, & B. Worzel (Eds.), Genetic programming theory and practice II (pp. 207-223). NY: Springer.
Moyaux, T., & McBurney, P. (2006). Reduction of the bullwhip effect in supply chains through speculation. In C. Bruun (Ed.), Advances in artificial economics: The economy as a complex dynamic system. Lecture Notes in Economics and Mathematical Systems Series, Volume 584 (pp. 77-89). Berlin, Germany: Springer.
Nienhaus, J., Zeigenbein, A., & Schoensleben, P. (2006). How human behaviour amplifies the bullwhip effect. A study based on the beer distribution game online. Production Planning & Control, 17 (6), 547-557.
O’Donnell, T., Maguire, L., McIvor, R., & Humphreys, P. (2006). Minimizing the bullwhip effect in a supply chain using genetic algorithms. International Journal of Production Research , 44 (8), 1523-1543.
Sammidi, S. (2008). Cost and profit analysis of supply chain ordering strategies to minimize the bullwhip effect using beer game. Indiana State University: MS in Industrial Technology Major Project.
Sarode, A. D., & Khodke, P. M. (2009). Performance measurement of supply chain management: A decision framework for evaluating and selecting supplier performance in a supply chain. The International Journal of Applied Management and Technology , 8 (1), 1-21.
Simchi-Levi, D., Kaminsky, P., & Simchi-Levi., E. (2007). Designing and managing the supply chain: Concepts, strategies, and case studies (3rd ed.). Boston, MA: Irwin McGraw-Hill.
Steckel, J. H., Gupta, S., & Banerji, A. (2004). Supply chain decision making: Will shorter cycle times and shared point-of-sale information necessarily help? Management Science , 50 (4), 458-464.
Sterman, J. D. (1989). Modeling managerial behavior: Misperception of feedback in a dynamic decision making experiment. Management Science , 35 (3), 321-339.
Sterman, J. (1992). Teaching takes off: Flight simulators for management education. OR/MS Today , October, 40-44.
Torres, O. A. C., & Moran, F. A. V. (2006). The bullwhip effect in supply chains: A review of methods, components and cases. New York: Palgrave Macmillan.
Towill, D. R., Zhou, L., & Disney, S. M. (2007). Reducing the bullwhip effect: Looking through the appropriate lens. International Journal of Production Economics , 108 (1-2), 444-453.
Vonk, E., Jain, L. C., & Johnson, R. P. (1997). Automatic generation of neural network architechture using evolutionary computation. Advances in fuzzy systems - Applications and theory, Vol. 14. River Edge, NJ: World Scientific.
Warburton, R. D. H., Hodgson, J. P. E, & Kim, Y. K. (2004). An analytical investigation of the bullwhip effect. NTC Project: S03-MD13s, National Textile Center Annual Report.