JITE v44n3 - An Instructional Strategy for Pictorial Drawing

Volume 44, Number 3
Fall 2007


An Instructional Strategy for Pictorial Drawing

Dr. James L. Mohler
Purdue University

Abstract

This contribution presents two major findings from a qualitative investigation into spatial ability. The elicited data suggested that one of the significant differences between individuals identified as high and low in spatial ability was their decomposition skill relative to spatial problems. Also revealing was the impact of frustration and anxiety on spatial functioning. The author discusses an instructional strategy for pictorial drawing that appeared effective for individuals solving pictorial drawing problems.

Introduction

With over 100 years of literature on the subject, it is no surprise that many studies have reported the positive effects of direct and indirect instruction on spatial ability ( Blade & Watson, 1955 ; Burnett & Lane, 1980M ; Coleman & Gotch, 1998 ; Ferrini-Mundy, 1987 ; Khoo & Koh, 1998 ; Kyllonen, Lohman, & Snow, 1984 ; Kyllonen, Lohman, & Woltz, 1984 ; Languis, 1998 ; Lord, 1985 ; Miller and Bertoline, 1991 ; Poole & Stanley, 1972 ; Rhoades, 1981 ; Rovet, 1983 ). Most researchers agree that spatial ability is a trainable attribute ( Tillotson, 1984 ).

Even a transient review of the literature on spatial ability yields hundreds of papers that discuss myriad spatial improvement activities and approaches. A few examples of these include traditional paper and pencil ( Newlin, 1979 ), physical models ( Miller, 1992 ), 2D CAD ( Mack, 1995 ), 3D CAD ( Shavalier, 2004 ), 3D animation ( Wiebe, 1993 ), and computer games ( Dorval & Pepin, 1986 ).

As reported by many researchers, context-specific direct instruction yields the best results ( Baldwin, 1985 ; Conner, Serbin & Schackman, 1977 ; Friedlander, 1985 ; Smith & Litman, 1979 ; Smith & Schroeder, 1979 ; Tillotson, 1984 ). Most pedagogical methods focus on spatial relations or spatial visualization activities. The former requires the mental manipulation of envisioned objects (e.g., rotating or moving them). The latter uses a variety of stimulus visuals that require the creation of alternative representations.

Aside from the practical methods employed, literature shows that spatial ability instruction is effective at nearly every instructional level. Clements, Battista, Sarama, and Swaminathan (1997) examined elementary students and found that instruction had a strong positive effect on student spatial ability (with respect to accuracy and number of items completed). A variety of studies also found that spatial instruction was effective with middle school students ( Ben- Haim, 1983 ; Ben-Haim, Lappan & Houang, 1985 ; Ben-Chaim, Lappan & Houang, 1988 ), reporting that all middle-school children benefited considerably from participation in spatial activities. Similarly, instruction has been found to be effective with high school students ( Battista, 1990; Geban, Askar, & Ozkan, 1992 ; Gurny, 2003 ) and post-secondary learners also ( Aldahmash, 1995 ; Braukmann & Pedras, 1993 ; Lord, 1983 , 1985 ; Small & Morton, 1983 ). Of particular noteworthiness, spatial ability is drastically affected by even limited amounts of spatial training. Rovet (1983) stated that, “it appears that 12 minutes of instruction was roughly equivalent to three years of untutored development” (p. 171).

Potential Qualitative Insights

That quantitative research dominates the spatial literature is no surprise. From its psychometric beginnings ( Carroll, 1993 ) to current information processing approaches ( Kyllonen, 1984 ), spatial ability research has a long quantitative history. Within the span between are a variety of other approaches including developmental ( Harris, 1979 ), strategic ( Lohman & Kyllonen, 1983 ), and differential ( Harris, 1978 ) perspectives, most of which utilize quantitative methodologies.

However, qualitative methods have yet to be extensively applied to this expansive area of research. Qualitative studies are rare in spatial research, even though they have the potential of providing rich insights and complementing well, the tradition that dominates the literature. Well-known quantitative researchers have acknowledged this ( Lohman & Kyllonen, 1983 ), encouraging researchers to engage in such studies.

Outside the spatial arena, qualitative inquiry has a lengthy history; most notably within education, psychology, and sociology. At its core, this mode of inquiry focuses on themes, patterns, concepts, insights, and understandings by using naturalistic, realworld situations, unfolding their depth and revealing their richness through introspection. Qualitative research is context-specific and generalizable to the extent that the context and situations are similar in the comparisons. Moreover, qualitative research focuses on questions that ask “what” or “how” rather than “why.”

Of the fundamental differences between qualitative and quantitative research and the respective questions each seeks to answer, Van Manen (1990) deftly explains:

…we are less interested in the factual status of particular instances: whether something happened, how often it tends to happen, or how the occurrence of an experience is related to the prevalence of other conditions or events. For example, phenomenology does not ask, “How do these children learn this particular material?” but it asks, “What is the nature or essence of the experience of learning (so I can now better understand what this particular learning experience is like for these children)? (p. 10)

A Qualitative Investigation of Spatial Ability

This contribution discusses an instructional strategy for pictorial drawing that emerged from a qualitative study into spatial ability. While the major qualitative themes and phenomenological description of spatial ability from the study is reported elsewhere ( Mohler, 2007 ), the most significant practical result is presented here – a problem solving approach for pictorial drawing. The goal of the overall study from which the finding resulted was to investigate the differences between the spatial experiences of those classified as high and low in spatial ability. The study used a phenomenological framework to study spatial ability as encountered by freshman engineering students; phenomenology is a specific type of qualitative research methodology where phenomena are examined through individual experience. Questions central to this research were:

  1. What do students report as their personal background (gender, parental occupation, parental involvement, or family income) that could have contributed to their strength or weakness in spatial ability?
  2. What personal experiences (hobbies and childhood or teenage experiences) or academic experiences (favorite courses, teachers or subjects) have contributed to their ability or inability?
  3. How do students approach spatial activities given their level of spatial ability, that is, what are their attitudes, thought processes, and perceptions surrounding such activities?

Methodology

The sample for this study was selected from students in the Computer Graphics Technology course CGT 163: Introduction to Graphics for Manufacturing during the spring semester of 2006 at Purdue University’s West Lafayette campus. CGT 163 was predominantly populated with freshman engineering students and it focused on freehand sketching and computer-aided design (CAD) to convey engineering ideas.

Extreme or deviant case sampling ( Patton, 2002 ) was used to select study participants; high and low spatial ability was determined using the Vandenberg Mental Rotations Test (1971) due to its reliability, validity, and convenience. Qualitative literature suggests between six and 10 participants ( Creswell, 1998 ; Dukes, 1984 ; Morse, 1994 ; Riemen, 1986 ). Therefore, 12 students were selected o participate in in-depth interviews; and eight students participated in one of two focus groups, totaling 20 participants in all.

Relevant to this article was the emergence of an instructional method to help students create pictorial drawings from multiview drawings, a task common in engineering graphics. The method resulted as a unique finding related to the third study question and as a result of think aloud tasks. It was corroborated through triangulation with the other data sources (interviews, observations, and focus groups). The remainder of the paper presents how the method emerged, the steps of the method, and some preliminary data in response to its use. The article concludes with opportunities for future investigations relative to the findings.

Think-aloud Tasks

While this phenomenological study included several data sources, one source was derived from engineering drawing problems that the participants solved during an interview. As the participants solved the problems, they were required to use a think-aloud technique, sometimes called a talk-aloud procedure. During this process, the participant speaks aloud their mental thoughts as they do some behavioral task ( Lodge, Tripp, & Harte, 2000 ; Nielson, Clemmensen, & Yssing, 2002 ). Concurrently, the researcher records the narrative, while also observing the participant and writing supplementary notes. The think-aloud sessions are then transcribed and qualitatively analyzed, along with the other data sources. Through analysis, the qualitative researcher looks for trends, themes, consistencies, and discrepancies ( Giorgi, 1985 , 1997 ).

During the think-aloud sessions, participants were given 90- minutes to solve three different engineering drawing problems. As shown in Figure 1, one problem required the creation of multiviews from a pictorial, while the other two problems required the creation of isometric pictorials from multiviews.

Nearly all of the participants were able to solve the multiview problem. Except for an occasional forgotten or incorrect line, both high and low spatial ability participants were able to correctly solve the general basis of the problem. As for the isometric pictorials, however, nearly all of the low ability participants were unable to solve them.

At the conclusion of the think-aloud interviews, the researcher provided feedback to the participants on their solutions and their process for creating them. In the case of the low ability participants, many were unable to complete much (if any) of the pictorial problems. Therefore, the extra time was used instructionally. The researcher talked through and solved the problems for the participants, describing things that the participant could do to improve their spatial problem solving skills. Following the data analysis, the researcher was able to recognize significant differences between those deemed high and low in ability, but it was the instructional aspect of the think-aloud tasks that revealed the most significant finding. The researcher realized that the high ability participants were using a consistent process in solving the pictorial problems and it was that same process that the researcher was repeating, albeit unknowingly, over and over during the instructional sessions with the low ability participants.

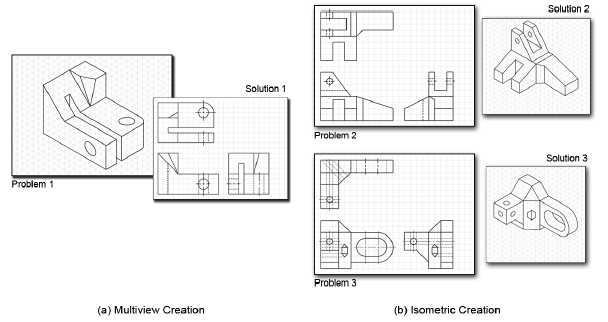Six images in three pairs. On the left problem one is next to solution 1. on the right problem 2 is next to solution two and below them problem 3 is next to solution 3.
Figure 1. Participants solved (a) one multiview creation problem and (b) two isometric pictorial problems while using a think-aloud technique.

Realizing “What is Going on Here?”

The researcher concluded that the major difference between the high and low spatial ability participants was their ability (or lack thereof) in deconstructing spatial representations into simpler, more manageable pieces so that they could solve them. As well, the pictorial drawing process appeared to not only assisted low ability participants in decomposing objects more easily, but it also provided a scaffolding mechanism that would enable a low ability participant to solve the pictorial problems even if they could not mentally decompose the problem. At the end of the study, the low ability participants reported that the process was enlightening, helpful, and that they gained positive results from utilizing it.

Questioning, Decomposition, and Frustration

Individuals with high spatial ability can often picture in the mind the solutions shown in Figure 1 , based upon the respective problem drawings. However, depending on their spatial capability, others may only be able to visualize certain portions of the object. Nevertheless, it is highly desirable that students develop cognitively—to the point of being able to visualize fully the pictorials from multiviews and vice versa. However, with the wide range of ability levels (and indeed when learning to visualize), it is more likely that students will not be able to visualize the entire object.

Listening to the high ability participants think-aloud narrative (and watching the low ability participants struggle immensely), the researcher realized that low ability participants needed a method for breaking down objects so they could visualize pieces of it. This was the first part of being able to create the pictorial drawing.

As was observed in this study, too often low ability participants got frustrated with the fact that they could not visualize the entire object—they got frustrated to the point of shutting down or giving up on the problem before they had ever drawn a single line on the page! But even the high ability participants (and the course instructor) acknowledged the importance of breaking the problem down into pieces, rather than trying to visualize the entire object from the start. When dealing with problem 2 and 3, nearly all of the high ability participants acknowledged decomposing the problem to solve it. The low ability participants either did not know that it was all right to do this, or they simply could not figure out how to do it, leading to significant frustration.

The researcher realized that there were some critical questions that participants could ask themselves (or be asked by someone else) that would help them begin solving complex spatial problems. The first question was whether they could visualize the entirely of the object. While seeming to be an obvious question, learners need to realize that if they can not visualize the entirety of an object in a spatial problem, it is ok. A related finding in this study was the crippling effect that frustration had on spatial thinking, particularly for low ability individuals. During the think-aloud sessions, reassurance had a dramatic effect on the low ability participants. Left alone, many low ability participants exhibited anxiety and frustration, which in turn disabled their spatial thinking, not to mention its impact on their motivation. But when reassured that visualizing a problem in chunks was acceptable (rather than holistically), their frustration and anxiety was visibly reduced.

Instead of becoming frustrated, learners need to stop and attempt to decompose an object mentally—to envision smaller chunks of the object. Figure 2 shows a visual example of how a spatial problem may be decomposed into simpler parts.

The 3-D geometric design of problem two with its four component parts seperated.
Figure 2. Problem 2 decomposed into its component parts.

Most of the low ability participants seemed to understand the concept of decomposition and, based on their comments, had “never thought of it that way.” Once decomposed in this way, the object could be initiated by drawing any of the three primary pieces shown in Figure 2 .

Then again, decomposition was not the only low ability participant problem that presented itself. Even if they could decompose the object, low ability participants seemed unsure how to draw the multiple pieces of the object in relation to one another; two participants actually made specific comments to this effect. Therefore, the researcher also went on to describe to them that whether or not they could mentally deconstruct an object, they could still create the pictorial using the pictorial drawing process.

The Pictorial Drawing Process (PDP)

The first step in the PDP is to create the pictorial box and center it on the page. Nearly all of the participants in the study used an isometric box, as shown in Figure 3 , to start their drawing. Figure 3 shows the construction box as a dashed line for clarity.

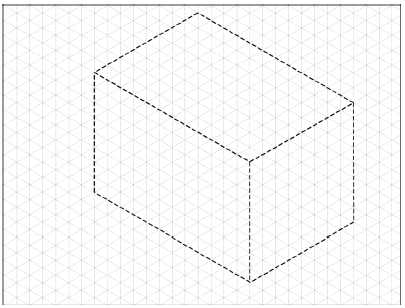A 3-D isometric box.
Figure 3 . Creation of the construction box for the isometric pictorial.

While all of the participants started problem 2 with an isometric box, all had difficulty centering it on the page. Therefore, the researcher realized that the following suggestions would help with centering the box on the page:

  • If the front view is wider than the right side view, start the front edge of the box to the right of center (the greater the size difference the farther to the right the front edge will be).
  • If the front view is smaller than the right side view, start the front edge of the box to the left of center (the greater the size difference, the farther to the left the front edge will be).

Ex post facto, all participants reported that these rules were quite helpful in centering the object. Fortuitously, all participants had a major sketching exam not long after the think-aloud interviews. All participants reported that the previous suggestions enabled them to correctly center their isometric pictorials on the paper.

Step 2 of the PDP stated that all features were reduced to prismatic elements. This was predominantly aimed at objects with large cylindrical or conical features. While problem 2 had none of these, problem 3 was an example that did (e.g., examine the large loop feature in Figure 1b).

Step 3 of the process required that participants draw all of the planes of the object that were coplanar with the isometric box faces. When working with the low ability participants, the researcher quizzed them on which faces were and were not coplanar with the isometric box. Figure 4 shows an example of the faces from problem 2 that would have been drawn.

The next step was to draw the lines that were coplanar with the left, back, and bottom planes of the isometric box. While this was a little more difficult for the low ability participants, the researcher again quizzed them on which lines were both visible and coplanar with the isometric box faces. Figure 5 shows the lines from problem 2 that qualified.

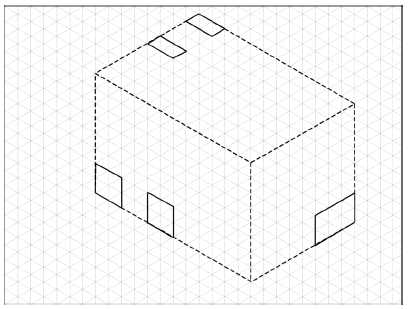The 3-D isometric box with the lines that were visable and coplanar from problem 2 outlined.
Figure 4 . In step 3, the faces that are coplanar with the isometric box planes are drawn.
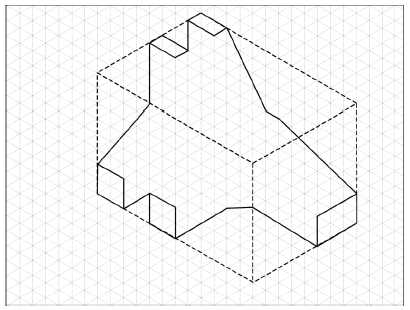The faces of the isometric box that are coplaner are drawn with the rest of the box cut away.
Figure 5 . In step 4, the lines that are coplanar with the left, back, and bottom of the isometric box are drawn.

Step 5 required that any remaining planar normals be drawn. Planar normals are those planes that are parallel to the isometric box planes, but do not lie in the isometric box planes. Figure 6 shows the one plane that was added to the drawing.

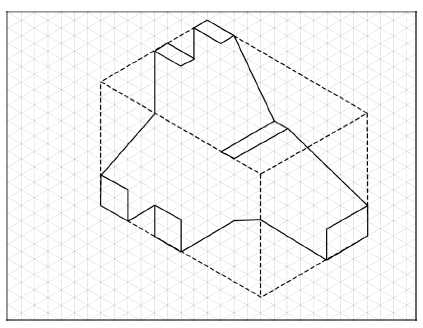The faces of the isometric box that are coplaner and the planar normals are drawn with the rest of the box cut away.
Figure 6. Adding the planar normals was the next step

In Step 6, inclined surfaces are added to the drawing. Problem 2 had several inclined (angled) surfaces. While drawing the inclined surfaces, the researcher provided instruction on finding the termination points on the slots, another aspect of difficulty. Figure 7 shows the solution for problem 2 with the inclined surfaces added.

Oblique planes are typically one of the most difficult things to draw in isometric. An oblique plane is a plane that is not true size or shape in the problem’s orthographic views (front, top, right side). In step 7, oblique planes were added to the drawing, as shown in Figure 8 .

While problem 2 had no cylindrical or conical features, step 8 would add these types of features to the drawing. Step 9, on the other hand, added negative geometry, as shown in Figure 9 (two holes).

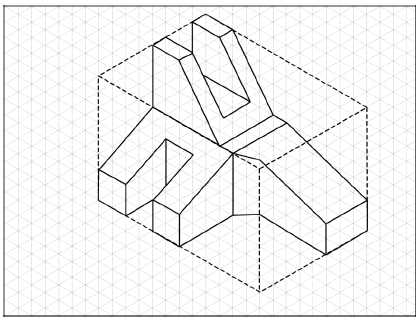The faces of the isometric box that are coplaner, the planar normals, and the inclined surfaces are drawn with the rest of the box cut away.
Figure 7 . Inclined surfaces are added to the drawing.

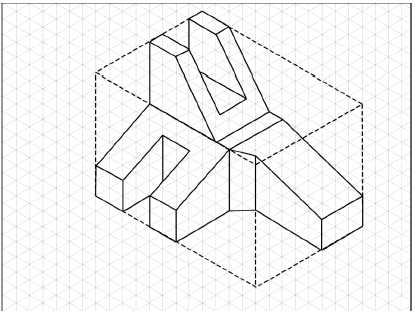The faces of the isometric box that are coplaner, the planar normals, the inclined surfaces, and the oblique planes are drawn with the rest of the box cut away.
Figure 8 . Oblique planes are added to the drawing in step 7.

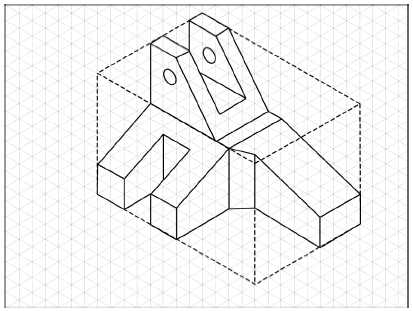The faces of the isometric box that are coplaner, the planar normals, the inclined surfaces, oblique planes, and negative geometry (such as holes) are drawn with the rest of the box cut away.
Figure 9 . Step 9 adds remaining negative geometry, such as holes.

The last step in the process was for the participant to review their solution for accuracy. The researcher encouraged all the participants, but particularly the low ability participants, to stop and check their drawing when completed.

Student Evaluation of the PDP

In the third and final interview of the study, several of the low ability participants acknowledged how helpful and beneficial the PDP was. The PDP had impact because the students did not have a defined process for pictorial creation. They had no scaffolding or procedure to use on complex objects. One participant said a pictorial creation process had not been taught in the course:

...as I said, that [pictorial drawing] is pretty hard to verbalize, because I don't think I could verbalize that to someone, and I don't know how they [instructors in CGT 163] could necessarily verbalize it to us. But, you know, with going from a 3D view or going from a pictorial to multiviews, you can see that a little easier cause you can like see the shape, like right in front of you, and kind of like, going from the views up. Sometimes it’s just very hard for anyone to just like get it right away. And I don't even know if there is a method, like, for them to teach us but like, their not doing it now if there is one.

However, later in the interview, the same participant said that the PDP helped her:

...when you taught me the method for the pictorial views, or going from multiview to the pictorial, I kind of thought, "Oh! That's how you do it." Kind of, or it’s like, how you can start from like pieces and put them together. I thought that was, I mean, very helpful because I don't think like if I had done that, or if you had taught me that I would, I would still be struggling with them today.

Similarly another participant said:

Um, that whole thing when you explained to me about the planes actually touch [the isometric box planes]…that helped me so much because before, I don't know, when I pictured it, I couldn't picture, like decipher between the ones that were like flat up against it and the ones that were pushed back and it kind of got jumbled in my head. And I don't know, that just made it a lot clearer.

Due to the limitations of this study, the researcher was unable to do much more than discover the PDP as it emerged from the data. While the prior participant comments are encouraging, after presenting the PDP it would have been beneficial to do additional applied, think-aloud problems to determine the effects (or range of effects) of the process on the participants.

The acknowledgement of the PDP raised several questions that could be pursued in future studies:

  1. Was the process useful to all types of pictorial drawing problems, or just specific types?
  2. To what degree did the student become more efficient or effective in creating pictorials?
  3. Did the process help the students develop their spatial skills to a point where the process is no longer needed as their spatial ability improves?
  4. Are there other alternative, part-dependent processes that high ability participants used?
  5. With refinement, could the pictorial drawing process affect all low ability participants?
  6. Does a similar process exist for complex multiview creation problems?

These are some of the questions that future studies should investigate. Nevertheless, the emergence of this process seemed to be an important finding in this study and has several implications for how engineering students are taught pictorial drawing.

Summary

This study has presented two of the findings from a qualitative study on spatial ability. The data suggest that one of the significant differences between individuals high and low spatial ability is their ability or inability in object decomposition. Important also was the impact that frustration and anxiety had on spatial functioning. It is the author’s recommendation that the pictorial drawing process described in this contribution be used as a teaching methodology. Moreover, additional studies should be conducted to evaluate its merit beyond the initial participant responses documented in this article.

References

Aldahmash, A. H. (1995). Kinetic vs static computer-generated visuals for facilitating college students’ understanding of reaction mechanisms in organic chemistry. Dissertation Abstracts International, 56 (8), 3069.

Baldwin, S. L. (1985). Instruction in spatial skills and its effect on math achievement in the intermediate grades. (Doctoral dissertation, University of Northern Colorado, 1984). Dissertation Abstracts International, 46 (3), 595.

Battista, M. T. (1990). Spatial visualization and gender differences in high school geometry. Journal for Research in Mathematics Education, 21 (1), 47-60.

Ben-Chaim, D., Lappan, G., & Houang, R. T. (1988). The effect of instruction on spatial visualization skills of middle school boys and girls. American Educational Research Journal, 25 (1), 51-71.

Ben-Haim, D. (1983). Spatial visualization: Sex differences, grade level differences and the effect of instruction on the performance and attitudes of middle school boys and girls. (Doctoral dissertation, Michigan State University, 1982). Dissertation Abstracts International, 43 (9), 2914.

Ben-Haim, D., Lappan, G., & Houang, R. T. (1985). Visualizing rectangular solids made of small cubes: analyzing and effecting students’ performance. Educational Studies in Mathematics, 16 , 389-409.

Blade, M. F., & Watson, W. S. (1955). Increase in spatial visualization test scores during engineering study. Psychological Monographs, 69 (12), 1-13.

Braukmann, J., & Pedras, M. J. (1993). A comparison of two methods of teaching visualization skills to college students. National Association of Industrial and Technology Teacher Educators, 30 (2), 65-80.

Burnett, S. A., & Lane, D. M. (1980). Effects of academic instruction on spatial visualization. Intelligence, 4 , 233-242.

Carroll, J. B. (1993). Human cognitive abilities: A survey of factoranalytic studies. New York: Cambridge University Press.

Clements, D. H., Battista, M. T., Sarama J., & Swaminathan, S. (1997). Development of students’ spatial thinking in a unit on geometric motions and area. The Elementary School Journal, 98 (2), 171-186.

Coleman, S. L., & Gotch, A. J. (1998). Spatial Perception Skills of Chemistry Students. Journal of Chemical Education, 75 (2), 206- 209.

Conner, J. M., Serbin, L. A., & Schackman, M. (1977). Sex differences in children’s response to training on a visual-spatial test. Developmental Psychology, 13 (3), 293-294.

Creswell, J. W. (1998). Qualitative inquiry and research design: Choosing among five traditions. Thousand Oaks, CA: Sage Publications.

Dorval, M., & Pépin, M. (1986). Effect of playing a video game on a measure of spatial visualization. Perceptual Motor Skills, 62 , 159-162.

Dukes, S. (1984). Phenomenological methodology in the human sciences. Journal of Religion and Health, 23 (3), 197-203.

Ferrini-Mundy, J. (1987). Spatial training for calculus students: Sex differences in achievement and in visualization ability. Journal for Research in Mathematics Education, 18 (2), 126-140.

Friedlander, A. (1985). Achievement in similarity tasks: Effect of instruction, and relationship with achievement in spatial visualization at the middle grades level. (Doctoral Dissertation, Michigan State University, 1984). Dissertation Abstracts International, 45 (12), 3570.

Geban, O., Askar, P., & Ozkan, I. (1992). Effects of computer simulations and problem-solving approaches on high school students. Journal of Educational Research, 86 (1), 5-10.

Giorgi, A. (1997). The theory, practice and evaluation of the phenomenological methods as a qualitative research procedure. Journal of Phenomenological Psychology, 28 , 235-260.

Giorgi, A. (Ed.). (1985). Phenomenology and psychological research. Pittsburgh, PA: Duquesne University Press.

Gurny, H. G. (2003). High school students' performance on Vandenberg's Mental Rotations Test: Art ability, gender, activities, academic performance, strategies, and easy of taking the test. Unpublished Master’s Thesis, College of New Rochelle, New York.

Harris, L. J. (1978). Sex differences in spatial ability: Possible environmental, genetic, and neurological factors. In M. Kinsbourne (Ed.), Asymmetrical function of the brain (pp. 405- 521). London: Cambridge University.

Harris, L. J. (1979). Sex-related differences in spatial ability: A developmental psychological view. In C. B. Kopp & M. Kilpatrick (Eds.), Becoming female: Perspectives on development (pp. 133-181). New York: Plenum Press.

Khoo, G. S., & Koh, T. S. (1998). Using Visualization and Simulation Tool in Tertiary Science Education. Journal of Computers in Mathematics and Science Teaching, 17 (1), 5-20.

Kyllonen, P. C. (1984). Information processing analysis of spatial ability. (Doctoral Dissertation, Stanford University, 1984). Dissertation Abstracts International, 45 (3), 819.

Kyllonen, P. C., Lohman, D. F., & Snow, R. E. (1984). Effects of Aptitudes, Strategy Training, and Task Facets on Spatial Task Performance. Journal of Educational Psychology, 76 (1), 130- 145.

Kyllonen, P.C., Lohman, D. F., & Woltz, D. (1984). Componential Modeling of Alternative Strategies for Performing Spatial Tasks. Journal of Educational Psychology, 76 (6), 1325-1345.

Languis, M. L. (1998; May). Using knowledge of the brain in educational practice. NASSP Bulletin, 82 , 38-47.

Lodge, J., Tripp, G., & Harte, D. K. (2000). Think-aloud, thoughtlistening, and video-mediated recall procedures in the assessment of children’s self-talk. Cognitive Therapy and Research, 24 (4), 399-418.

Lohman, D. F., & Kyllonen, P. C. (1983). Individual differences in solution strategy on spatial tasks. In R. F. Dillon & R. R. Schmeck (Eds.), Individual differences in cognition (Vol. 1, pp. 105-135). New York: Academic Press.

Lord, T. R. (1983). The effects of visual-spatial aptitude on the study of college biology. Dissertation Abstracts International, 44 (8), 2430.

Lord, T. R. (1985). Enhancing the visuo-spatial aptitude of students. Journal of Research in Science Teaching, 22 (5), 395-405.

Mack, W. E. (1995). Computer-aided design training and spatial visualization ability in gifted adolescents. Journal of Technology Studies, 21 (2), 57-63.

Miller, C. L. (1992a). The results of integrating real and computer generated models into a traditional sketching based engineering graphics course. Engineering Design Graphics Journal, 56 (2), 27-47.

Miller, C. L., & Bertoline, G. R. (1991). Spatial visualization research and theories: Their importance in the development of an engineering and technical design graphics curriculum model. Engineering Design Graphics Journal, 55 (3), 5-14.

Mohler, J. L. (2007). A phenomenological examination of spatial ability. Proceedings of the 61st Annual Engineering Design Graphics Division Mid-year Meeting (pp. 123-136). Washington, D. C.: ASEE.

Morse, J. M. (1994). Designing funded qualitative research. In N. K. Denzin & T. S. Lincoln (Eds.), Handbook of qualitative research (pp. 220-235). Thousand Oaks, CA: Sage.

Newlin, C. W. (1979). The total concept of graphics and design in the engineering curriculum. Engineering Design Graphics Journal, 43 (2), 21-22.

Nielson, J., Clemmensen, T., & Yssing, C. (2002). Getting access to what goes on in people’s heads: Reflections on the think-aloud technique. Proceedings of the second Nordic conference on Human-computer interaction , October 19-23, 2002, Aarhus, Denmark.

Patton, M. Q. (2002). Qualitative evaluation and research methods (3rd ed.). Thousand Oaks, CA: Sage Publications.

Poole, C., & Stanley, G. (1972). A factorial and predictive study of spatial abilities. Australian Journal of Psychology, 24 (3), 317- 320.

Rhoades, H. M. (1981). Training spatial ability. In E. Klinger (Ed.), Imagery, concepts, results and applications (Vol. 2, pp. 247- 256). New York: Plenum Press.

Rieman, D. J. (1986). The essential structure of a caring interaction: Doing phenomenology. In P. M. Munhall & C. J. Oiler (Eds.), Nursing research: A qualitative perspective (pp. 85-105). Norwalk, CT: Appleton-Century-Crofts.

Rovet, J. (1983). The Education of Spatial Transformations. In D. R. Olson & E. Bialystok (Eds.), Spatial cognition: The structure and development of mental representations of spatial relations (pp. 164-181). London: Lawrence Erlbaum Associates.

Shavalier, M. (2004). The effects of CAD-like software on the spatial ability of middle school students. Journal of Educational Computing Research, 31 (1), 37-49.

Small, M. Y., & Morton, M. E. (1983). Spatial Visualization training improves performance in organic chemistry. Journal of College Science Teaching, 13 (1), 41-43.

Smith, W. S., & Litman, C. I. (1979). Early adolescent girls’ and boys’ learning of a spatial visualization skill. Science Education, 63 (5), 671-676.

Smith, W. S., & Schroeder, C. K. (1979). Instruction of fourth grade girls and boys on spatial visualization. Science Education, 63 (1), 61-66.

Tillotson, M. L. (1984). The effect of instruction in spatial visualization on spatial abilities and mathematical problem solving. (Doctoral Dissertation, The University of Florida, 1984). Dissertation Abstracts International, 45 (9), 2792.

Van Manen, M. (1990). Researching lived experience: Human science for an action sensitive pedagogy. New York: State University of New York.

Vandenberg, S. G. (1971). The Mental Rotations Test. Boulder: University of Colorado.

Wiebe, E. N. (1993). Visualization of three-dimensional form: A discussion of theoretical models of internal representation. Engineering Design Graphics Journal, 57 (1), 18-28.

James L. Mohler is an Associate Professor of the Department of Computer Graphics Technology at Purdue University. He can be reached at jlmohler@purdue.edu .