JTE v11n2 - Elementary Children's Awareness of Strategies for Testing Structural Strength: A Three Year Study
Elementary Children's Awareness of Strategies for Testing Structural Strength: A Three Year Study
Brenda J. Gustafson, Patricia M. Rowell and Sandra M. Guilbert
Brenda J. Gustafson (brenda.gustafson@ualberta.ca) is an Associate Professor in the Department of Elementary Education. Patricia Rowell (pat.rowell@ualberta.ca) is a Professor of Elementary Science Education in the Department of Elementary Education. Sandra M. Guilbert is a doctoral candidate in the Department of Elementary Education. All are with the University of Alberta, Edmonton, Alberta, Canada.
Introduction
In recent years there has been a trend towards including design technology in elementary school programs either as a separate subject area or as an addition to some existing science program. Design technology study is seen as a means for children to develop procedural and conceptual knowledge of devices created to fulfill a human need.
In Alberta, Canada a new Elementary Science Program ( Alberta Education, 1996 ) was mandated for use in September 1996. One feature of this new program was the inclusion of a Problem Solving Through Technology topic at each of the six grade levels. Problem Solving Through Technology topics were intended to promote children's development of skills and knowledge related to design technology ( Rowell, Gustafson, & Guilbert, 1999 a, b ).
The three year research project from which this paper is written commenced in September 1995; one year prior to the mandated implementation of a new Elementary Science Program ( Alberta Education, 1996 ). In this three year project, we asked elementary children to respond to Awareness of Technology Surveys , interviewed teachers, administrators and engineers, conducted case studies in classrooms, and involved children in performance based assessments related to the design technology topics. The scope and nature of this three-year research project is described in detail in previous publications ( Gustafson, Rowell, Rose (1999); Rowell, Gustafson, & Guilbert, 1999 a, b; Rowell & Gustafson, 1998 ).
Research Questions
In the research reported in this paper, we focus on one question from the Awareness of Technology Survey that was administered in Study Year One (September, 1995June, 1996) prior to the implementation of the new Alberta elementary science program. A revised version of this same survey question was re-administered to children in Study Year Three after they had participated in formal classroom experiences in Study Year Two related to the Problem Solving Through Technology topics. The survey question, named Jan's and Bob's Bridges, was designed to explore elementary children's awareness of strategies for testing the structural strength of bridges pictured in the survey. Analysis of the children's responses to this survey question allowed discussion of the following research questions:
- What is the nature of children's ideas about testing structural strength?
- How do children's perceptions of testing strategies change over time?
- Do young children's survey responses differ from those offered by older children?
- Are there any gender related differences between survey responses?
Related Literature
The theoretical underpinnings of this research are primarily drawn from constructivist learning theory and research into the nature and development of children's design technology problem solving skills.
Ideas from Constructivist Learning Theory
Constructivists view learning as a complicated endeavor influenced by the learner's existing ideas, the learner's willingness to engage intellectually in the task at hand, the socio-cultural context, and the teacher's pedagogical practice ( Appleton, 1997 ; Driver, 1989; Harlen & Jelly, 1989; Osborne & Freyberg, 1985 ). Constructivists believe that prior to formal classroom instruction children possess existing ideas that are sensible (to the children), strongly held and constructed from a number of sources and experiences ( Osborne & Freyberg, 1985 ). These existing ideas may prove helpful or unhelpful when children encounter new ideas in the classroom and draw upon existing knowledge to make sense of the encounter ( Appleton, 1997 ). In addition to recognizing the importance of existing knowledge, constructivists also lend support to the observation that children may participate in common classroom experiences and subsequently display a variety of interpretations of those experiences ( Appleton, 1997 ). The complex ways in which children use existing ideas to make sense of new situations and move towards some understanding or solution can help account for the variety and nature of children's ideas.
Ideas from Design Technology Research
Much design technology research has focussed on characterizing what children do to solve problems and arranging these actions into design technology problem solving models ( Bottrill, 1995 ; Johnsey, 1995, 1997 ; Layton, 1993 ; McCormick, 1996 ; Roden, 1997 ). Various terms have been used to describe children's problem solving actions. They include processes, procedures, procedural skills, facets of performance, facets of capability, problem solving skills, problems solving processes, and thinking processes ( Bottrill, 1995 ; Custer, 1995; Johnsey, 1997; Kimbell, Stables, & Green, 1996 ). Regardless of the label given to these actions, researchers tend to produce lists of actions or skills, sometimes arranged into problem solving models, which can include designing, making, trouble-shooting, repairing, inventing, testing, and evaluating. These problem solving models can then be used to direct teaching practice, assess children, and influence program development.
A skill commonly appearing in problem solving models and considered to be one facet of technological capability is evaluating or testing a product ( Kimbell, 1994 ). In the research presented in the paper, we have tended to view evaluating and testing as closely linked and capable of occurring concurrently ( Anning, 1994; Anning, Jenkins, & Whitelaw, 1996; Bottrill, 1995 ). Other researchers have distinguished between the two while emphasizing that both can occur during and at the end of an activity ( Kimbell, Stables, & Green, 1996 ). In reviewing a range of problem solving models, Johnsey (1995) showed that evaluating could involve: judging a solution against some specifications; identifying judging criteria; evaluating the effectiveness of a solution; critically appraising a solution inside the head; considering design ideas as they develop; appraising the efficacy of design activity, or; accepting or rejecting a solution. Testing could involve: testing the performance of a product; conducting trials; testing an outcome; validating and judging inside the head together with testing; testing a solution, or; assessing the effectiveness of a product ( Johnsey, 1995) . Evaluating and testing, therefore, do not appear mutually exclusive. At times these skills can blend together as children judge whether a device has met the original identified need, whether it exhibited appropriate resource use, and whether it made an impact beyond the purpose for which it was designed ( Anning, Jenkins, & Whitelaw, 1996; Kimbell, Stables, & Green, 1996; Tickle, 1990 ).
Evaluating or testing can occur during the process of reaching an effective solution and additionally involve summative evaluation of product success against design criteria ( Bottrill, 1995; Kimbell, Stables, & Green, 1996 ). In classroom situations, evaluating or testing allows children to reflect on the developing design and think about design strengths and weaknesses once it has been completed ( Kimbell, Stables, & Green, 1996 ). In the present study, we explore testing or evaluation strategies that would likely occur during summative evaluation of a structure.
Age and Gender Issues in Design Technology
Researchers have observed that young children frequently display a reluctance to perform summative evaluation or testing and may have difficulty performing the cognitive tasks necessary for evaluation. Anning (1994) observed that teachers of young children found it unrealistic to expect children to perform summative evaluation. Children viewed this evaluation as "doing it again" and were reluctant to engage in this task. Evaluation was much more useful if it "permeated the whole iterative cycle of designing and making" ( Anning, 1994, p. 174) . Other researchers have agreed that Key Stage 1 (ages 5-7) children prefer to respond to problems on an ongoing basis and see less need to perform summative evaluation on their finished products ( Kimbell, Stables, & Green, 1996) .
Product evaluation and testing involves complex cognitive demands. Kimbell (1994) describes these demands as encompassing an understanding of materials, tools, and processes then using this knowledge to make a product and evaluate it critically against the needs of the user. This can be a daunting task for young children. Other researchers observe that young children can show a reluctance to test or evaluate their work because they lack the mental models against which to make informed judgements or resist the requirement to think deeply or are unaware of appropriate evaluation criteria ( Anning, 1994; Anning, Jenkins & Whitelaw, 1996 ). Clearly, researchers perceive differences between evaluation conducted by children of different age groups. Kimbell (1994) warns, however, that caution should be used when assigning criteria of capability based on children's ages. Perceived capability in testing or evaluating could be influenced by any number of factors known to play a role in children's understanding of constructing.
Fewer studies have been conducted on gender differences in design technology ( Kimbell, Stables, & Green, 1996; Ross & Brown, 1993) . An observation pertinent to the present study is that in general, girls do better than boys in the more reflective areas of design technology work. An example of these more reflective tasks includes testing and evaluating products in terms of their performance and fit with evaluative criteria.
Study Framework
In this section, we provide a brief overview of the Alberta program followed by information about study methodology.
Alberta Program
As mentioned earlier, in September 1996 a new Alberta Elementary Science Program (1996) was mandated for use in Alberta schools. The program featured four Science Inquiry (SI) topics and one Problem Solving Through Technology (PST) topic at each of the six grade levels. The Problem Solving Through Technology topics were intended to show links between science and technology through allowing children to participate in design technology activities created to promote technological problem solving capability and conceptual knowledge. In each grade level, a Problem Solving Through Technology problem solving model was outlined which arranged technological problem solving skills under three headings: Focus; Explore and Investigate, and Reflect and Interpret. A Science Inquiry (SI) problem solving model in which skills were outlined under the same three headings was also included in the program. These models were followed by the topics for the grade and a list of General and Specific Learner Expectations (GLEs and SLEs) written in behavioral terms describing activities related to the topics.
In Grade One, the PST model provides no specific mention of evaluating or testing. Instead, the Building Things topic asks children to select materials and construct objects such as buildings, furniture, vehicles, and wind and water related artifacts. These building activities quite naturally involve the ongoing evaluation of materials and methods of fastening despite the lack of acknowl-edgement of these skills in the problem solving model. Grade Two focuses on a Buoyancy and Boats topic which promotes building and testing a variety of watercraft, testing that leads to modifying a watercraft and evaluating the appropriateness of various materials. The PST model at this grade level reiterates that children should "identify steps followed in constructing an object and in testing to see if it works" ( Alberta Education, 1996, p. B6 ). Building With a Variety of Materials is the Grade Three PST topic frequently taught in conjunction with a Testing Materials and Designs science inquiry topic. These two topics ask children not only to construct and test structures that span gaps, but also to conduct tests to show how materials, shapes, and methods of joining effect the strength of structures. The Grade Four SI model mentions that children should "carry out, with guidance, procedures that comprise a fair test" ( Alberta Education, 1996, p. B17 ). The PST model states that children will "identify steps followed in completing the task and in testing the product" and "evaluate the product based on a given set of questions or criteria ( Alberta Education, 1996, p. B17, B18 ). Grade Four children participate in a Building Devices and Vehicles That Move topic which further requires them to explore and evaluate design variations of mechanical devices and models. In Grade Five, the SI model again mentions the importance of carrying out fair tests and the PST model asks children to "evaluate a design or product, based on a given set of questions or criteria" ( Alberta Education, 1996, p. B24 ). As Grade Five children work on Mechanisms Using Electricity , they use ongoing evaluation to construct electrical devices such as motion detectors and burglar alarms. Fair testing is again emphasized in Grade Six with children expected to evaluate procedures used and products constructed. The topic Flight provides a context in which children can build and test a number of flying devices such as designs for parachutes, gliders and propellers.
Clearly, the Alberta program provides opportunities for children to work in a number of contexts to develop evaluating and testing skills that would promote the development of technological capability. What is less clear is how Alberta teachers operationalized these program expectations during Study Year Two of this research project.
In order to provide insight into Study Year Two instruction, we conducted case studies in six elementary classrooms ( Rowell & Gustafson, 1998 ). Many of the children who responded to the Awareness of Technology Surveys were enrolled in these classrooms. Case studies showed most teachers struggled to understand the conceptual underpinnings of the design technology topics, were unfamiliar with the discourse of technological problem solving, tended to interpret technological problem solving models as similar to science inquiry models, and received little professional support for the development of necessary skills and understandings. Despite these challenges, generally teachers were enthusiastic about the design technology topics and the potential these topics held for extending children's understanding of technology and science.
Study Methodology
Instrument
The instrument used was named the Awareness of Technology Survey and featured questions intended to explore children's characterization of technology and knowledge of skills and concepts related to the Alberta program. Each of the six grade levels featured a different selection of questions related to program expectations with some questions, such as Jan's and Bob's Bridges, repeated at each grade level.
Awareness of Technology Survey questions were either created by the authors or patterned after similar questions posed in previous studies by other researchers ( Aikenhead, 1988 ; Coenen Van Den Bergh, 1987 ; DES, 1992 ; Gadd & Morton, 1992 a, b ; Harrison & Ryan, 1990 ; Rennie, 1987 ; Rennie, Treagust, & Kinnear, 1992; Symington, 1987 ). Working copies of questions were sent to provincial government personnel familiar with the new program who had experience with student assessment and test development. Comments from these consults were used to improve question structure and provide validation of survey questions with respect to the new program.Piloting
The Awareness of Technology Survey was piloted with a group of 140 children in grades one through six (ages 5-12). Grade One children who had yet to develop extensive reading skills had questions read to them as a whole group; this strategy was used despite the fact that the Grade One version of the survey featured little writing. Children's oral questions and advice as well as teacher comments were noted. Children's written survey responses were analyzed by study authors to check whether they addressed the original intent of the questions and revisions were made to the questions. This piloting experience allowed authors to construct the Awareness of Technology Survey used in Study Year One. A revised version of this same survey which eliminated some Study Year One questions and asked children to elaborate more on remaining questions was used in Study Year Three.
Selecting the Children and Administering the Survey
The Awareness of Technology Survey was administered in cooperation with a rural school system located adjacent to a large urban area. Classrooms and teachers were selected by the school system's Program Facilitator, who was careful to involve children from a variety of schools and grade levels. In Study Year One, 334 children (180 male, 154 female) from all six grade levels completed the survey. In order to assist Grade One children with reading the survey, a research assistant read the survey to each child and assisted with writing down the children's verbal comments. Teachers in other grade levels were asked to assist any children assigned to their classrooms who encountered reading difficulties.
In Study Year Three, children who had completed the Jan's and Bob's Bridges survey question in Study Year One were located and the revised version of the same question was asked of them. Those students who had been enrolled in Grade 6 in Study Year One were excluded from Study Year Three data collection since they would now be in Grade 7 (Junior High School). They would therefore not have participated in experiences related to the Problem Solving Through Technology topics in the elementary science program.
Study Focus
This research study explored strategies for testing structural strength proposed by elementary children before and after formal classroom instruction in Problem Solving Through Technology topics. Specifically, this research reports on children's responses to the Jan's and Bob's Bridges survey question that focused on how children might test the structural strength of two bridges which were presented to them in the form of illustrations, as shown in Figure 1.
JAN AND BOB EACH BUILT A BRIDGE ACROSS A SMALL STREAM 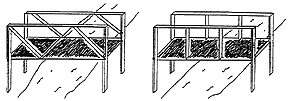
JAN'S BRIDGE BOB'S BRIDGE Figure 1. Illustrations of Jan's and Bob's Bridges as presented in the study. The questions asked of the children at the two levels of the study are presented in Table 1.
The focus was on 167 elementary children (83 male; 84 female) who completed this survey question in both Study Years One and Three (see Table 2). In Study Year One, these children were enrolled in Grades 1-5 (ages 5-11) and in Study Year Three were in Grades 3-7 (ages 8-14). Examining the same population in both years (while keeping in mind the unequal numbers of subjects between grades) allows judgements to be made about the degree to which participation in classroom activities in Study Year Two might have promoted children's testing and evaluation strategies.
Table 1
Questions Asked of Children at Study Year One and Study Year Three Study Year One Study Year Three Circle the strongest bridge. Circle the strongest bridge. How could you find out if your answer is correct? Why do you think this bridge is the strongest? What would you do to find out if your answer is correct? Results
In Study Years One and Three, children were asked to decide whether they thought Jan's or Bob's bridge was stronger and then propose a testing strategy which would confirm or possibly disprove their decision. Children's responses about testing strategies were read repeatedly and were ordered into five categories in terms of their usefulness for understanding the problem and components of fair testing. The children's responses ranged from indicating why the bridge was strong to suggestions involving elements of fair testing. The five categories are shown in Table 3.
Children in Category 1 could be viewed as having misread the question as they focused on describing why the bridge they circled was stronger than the other bridge rather than how to test for bridge strength. Some survey responses tended to focus on the obvious differences between the bridge railings and children variously judged either slanted or vertical railings as key to structural strength. For example, some children wrote:
- Because [up and down railings] can hold it up better.
- Because this one has squares and the other has diamond shapes.
- The posts go up and down.
Other children noticed Jan's bridge had three diagonal railings while Bob's had two vertical railings but it remained unclear how this would affect bridge strength.
- This one has more sticks [Jan's].
- This one [Bob's] has less sticks so it will hold people.
Some of the younger children in Category 1 seemed to have difficulty interpreting the three-dimensional picture. Some argued that their selected bridge was stronger because the wood was thicker or that one bridge was bigger than the other bridge. Although Category 1 responses did not address the issue of testing, they still provided some insight into children's notions of structural strength. Clearly, in trying to judge structural strength, some children thought that the orientation of structural components was critical while others believed the amount of materials used impacted on structural strength. Although component orientation is a key idea underpinning structural strength, the issue of material amount is more contentious. Adding more materials can, in some situations, increase the strength of the structure. But other factors, such as the type of material, how it is joined to the structure, and the way it is oriented within the structure, could all potentially influence whether additional materials do increase strength.
Table 2
Descriptive Statistics
Study Year 1 Response Category Grade Gender Mean Standard Deviation N 1 Male 1.48 .87 21 Female 1.25 .44 24 Total 1.36 .68 45 2 Male 1.77 1.24 13 Female 1.73 1.10 11 Total 1.75 1.15 24 3 Male 1.29 .47 17 Female 2.05 .91 19 Total 1.69 .82 36 4 Male 2.09 1.51 11 Female 2.00 1.41 17 Total 2.04 1.43 28 5 Male 2.20 1.01 20 Female 3.43 1.34 14 Total 2.71 1.29 34 Total Male 1.74 1.05 82 Female 2.00 1.24 85 Total 1.87 1.16 167 Study Year 3 Response Category Grade Gender Mean Standard Deviation N 3 Male 1.95 1.07 21 Female 1.96 1.00 24 Total 1.96 1.02 45 4 Male 2.54 .97 13 Female 2.45 .82 11 Total 2.50 .88 24 5 Male 2.88 1.11 17 Female 2.68 1.20 19 Total 2.78 1.15 36 6 Male 3.00 1.41 11 Female 3.12 1.50 17 Total 3.07 1.44 28 7 Male 2.70 1.34 20 Female 3.93 1.38 14 Total 3.21 1.47 34 Total Male 2.56 1.22 82 Female 2.74 1.36 85 Total 2.65 1.29 167 Table 3
Categories of Children's Responses
Category Description 1 Indicated why the bridge was strong; but not how to test the bridge 2 Concept of testing was weakly expressed (e.g., Build it; Test it.) 3 Testing concept developed, but fairness lacking (e.g., Add weights; Put toys on it; Shake it.) 4 A fair test but lacking all the items (exact same test for each bridge) 5 A fair test including weights and a measurement decision (e.g., addition of the element of measurement: how much weight could be added until one broke) Category 2 responses showed an awareness of testing but children seemed unsure about exactly what would constitute fair testing strategies. Some simply advised that one could camp, drive, walk or jump on the selected bridge, hit it with a hammer, kick it, or build it. Some children wrote:
- I would build the bridge and put pressure on the railing.
- Walking across it.
- I would put a small toy car on it.
No mention was made of comparing the two bridges or of specific criteria used to perform the test. Be that as it may, the children offered ideas that could form the beginning of good testing ideas.
The third response category included children who showed more development of testing strategies than the previous category in that some of them acknowledged the necessity of comparing the bridges, while others provided a few more details about the testing strategy. For example, some children wrote:
- Put some things on each of the bridges.
- Rock them back and forth.
- Walk across each bridge.
- I would find out if it was correct by putting something heavy on both of the bridges.
Through these responses children showed they realized that comparative testing was needed in order to judge which bridge was stronger. However, some did not include many details. Others did not mention continuing the test until some conclusive observations could be seen.
Category 4 included children who wrote about a fair test and the necessity to continue that test until some conclusion could be arrived at, but were still in need of clarifying some of the testing details. For example, children wrote:
- You could build them and test it with weight and see whose bridge falls down first.
- You could get lots of people to stand on each on and see which holds better.
- I would find out by tapping it a little bit and see which ones collapse.
Category 4 contained useful ideas simply in need of a few more details. The first child quoted above could be asked to clarify the manner in which the weights would be added to the bridges, the second child asked how people would be ordered onto the bridges, and the third child asked to outline the details of the tapping test. These added details would show the details of the fair testing procedure contained in the responses.
Children in Category 5 provided impressive fair testing ideas that included details about how to compare the relative strength of each bridge. One child suggested that, " you could put something [equal to] the weight of an averaged sized eleven year old child and put it on to see if it will brake or not then if they don't breke try going hever" [sic]. Another child responded in a similar vein that "you could put weights on the bridges and keep on putting weights on until one of the bridges broke." These responses show the children in this category had an understanding of fair testing similar to the expectations found by the Grade Five level of the Alberta program. The variety of written responses to the survey question provide insights into the first research question listed at the beginning of this paper.
Statistical analysis of children's coded responses was used to provide answers to the remaining three research questions and to help judge differences between study years, grades, and gender. In this way, it was hoped that some insight might be discovered of how children's perceptions of testing strategies might have changed over time, how younger children's answers compared to older children's answers, and whether there were any significant differences between boys' and girls' responses. Significant differences between these variables could provide some understanding of how population samples performed as well as the possible efficacy of Study Year Two instruction.
A 2X2 ANOVA using a repeated measures procedure was applied to Study Years One and Three data to examine the differences in students' performance on the Jan's and Bob's Bridges survey question. The obtained scores were assumed to be independent and normally distributed within each treatment level. The computed Greenhouse-Geiser epsilon value was 1.000 showing that the condition of sphericity in the repeated measures procedure was met. The results of the ANOVA are reported in Table 4.
Table 4
ANOVA Between Study Years One and Three
Test SS df MS F p Year 49.119 1 49.119 40.545 .000 Year*Grade 4.773 4 1.193 .985 .418 Year*Gender .243 1 .243 .201 .655 Year*Grade*Gender 4.273 4 1.068 .882 .476 Error (YEAR) 190.199 157 1.211 An overall significant difference ( p < .05) in students' performance on the Jan's and Bob's Bridges survey question between Study Years One and Three ( F (1, 157) = 40.545) was found. Tests of interactions (Year X Grade; Year X Gender; and Year X Grade X Gender) indicate that the difference between the two Study Years was uniform across the five grade levels and was not influenced by the respondents' gender.
The ANOVA of between-subject effects (see Table 5) reveals a significant interaction between gender and grade. This means that boys and girls performed differently to the survey question depending on grade level ( F (4,157) = 4.02). In particular, when all boys in the study are compared to all girls in the study (study years combined), boys outperformed girls in the lower grades while girls outperformed boys in the higher grades (see Table 6). Table 5 also shows a significant grade level effect ( F (4,157) = 15.72) which means students in different grade levels performed differently (see Table 6 for details between grades). To illustrate, Bonferroni post hoc tests for between-subject effects show significant differences in mean performance across two years of study between Grades 1 and 4 and between Grades 1 and 5 ( t (5,157) = -3.58, and t (5,157) = -4.91 respectively). Table 5 also features a marginal significant overall gender effect, meaning that when boys and girls in the two years of the study are combined, the genders perform differently. This marginal effect was further examined through planned post hoc multiple comparisons, which revealed that boys in Grades 4 and 5 together performed differently across the two years of study when compared to girls in the corresponding grades ( t (2,157) = -2.73).
Table 5
ANOVA of Between-Subjects Effects
Test SS df MS F p Intercept 1690.35 1 1690.35 1322.47 .000 Grade 80.38 4 20.10 15.72 .000 Gender 5.69 1 5.69 4.45 .036 Grade*Gender 20.57 4 5.14 4.02 .004 Error 172.52 157 1.10 Table 6
Table of Means: Mean Performances Across Gender and Grade (Study Years One and Three Combined)Bonferroni post hoc tests were conducted to examine differences in students' performances on the survey question over time at each grade level (see Table 7). The Bonferroni procedure was used because of its conceptual simplicity, flexibility, and ability to control Type 1 error when families of contexts are tested. The results indicated that the difference in performance on the survey question administered in Study Years One and Three was statistically significant (p < .05) for students who were in Grades 3 and 4 in Study Year One then Grades 5 and 6 in Study Year Three.
Gender Grade 1(3) Grade 2(4) Grade 3(5) Grade 4(6) Grade 5(7) Total Male 1.715 2.155 2.085 2.545 2.45 2.15 N=21 N=13 N=12 N=11 N=20 N=82 Female 1.60 2.09 2.365 2.56 3.18 2.37 N=24 N=11 N=18 N=12 N=14 N=85 Total 1.66 2.082 2.225 2.553 2.815 N=45 N=24 N=36 N=28 N=34 N=167 Table 7
Bonferroni Post Hoc Tests
Grade Mean Difference Bonferroni t ((5,157) 1-3 -.60 2.59 2-4 -.75 2.36 3-5 -1.09 4.20* 4-6 -1.03 3.50* 5-7 -.50 1.87 *p < .05 Discussion
The most useful part of this study lies in the range of survey responses offered by the children and the insight this provides into future classroom practice. Clearly, children hold a variety of ideas about how to test structural strength even before formal classroom instruction in this design technology skill. These ideas likely arise from prior experiences encountered during everyday life. The frequency of responses of the children among the five response categories developed for the study, however, revealed that children in all grade levels are in need of further assistance. Most responses in Study Years One and Three tended to fall into Categories 1-3 despite statistical analysis showing an overall significant difference between the two study years. Category 1 included ideas about why a bridge was stronger while Categories 2 and 3 included a beginning awareness of testing strategies. These ideas about strength and testing are potentially useful but still in need of further refinement. A productive use of classroom time would involve exploring children's existing ideas about testing strategies and helping children grow towards recognizing how a fair comparison between two structures would allow a more critical appraisal of the design. Another important idea following from the response categories involves the ordering of the categories. Through ordering children's responses we only sought to provide an interpretive framework for this research study. Suggesting that children's responses indicate sequential stages of understanding fair testing through which children progress is not supported by this study. Instead, we do not rule out that children could show many unanticipated routes and frequent reversals of thinking before arriving at a full understanding of fair testing. A similar argument questioning the sequential ordering of problem solving skills could also be applied to technological problem solving models depicted in school programs. Johnsey (1997) has argued that children tend to employ problem solving skills in a fairly random way and that skills are naturally intermixed as children work towards solutions. Others describe technological problem solving as a messy and somewhat internally chaotic experience bearing little resemblance to the stage models appearing in literature ( Ridgway & Passey, 1992 ; Rowell & Gustafson, 1998) . Clearly, problem solving models listing skills arranged in some sequence or series of stages may not provide an accurate picture of how children tackle classroom problem solving. Further, describing individual skill development as being comprised of some progressive sequence of thinking might be equally misguided. A second focus of this study was on the possible influence of experiences from Study Year Two on the children's responses over time. Study Year Two featured opportunities for children to participate in design technology units that should have included learning about evaluating and testing. As mentioned earlier, design technology topics in the Alberta program varied in their emphasis on testing and evaluating and featured the development of these skills within a number of different contexts. Also, teachers faced with implementing these topics in Study Year Two received little professional support, were inexperienced with concepts related to structural strength and skills such as testing, and found it challenging to interpret and teach the new program. Some researchers maintain that problem solving is a domain specific activity and that expertise in some skill in one context does not necessarily mean the skill can be transferred successfully to some other context ( McCormick, Hennessy, & Murphy, 1993 ; McCormick, Murphy, Hennessy, & Davidson, 1996 ). When this hypothesis is applied to the Alberta program, it means that children would need to revisit fair testing each year as they encountered different contexts within the program. Teachers would have to be cautious in assuming that children could use fair testing experiences to interpret contexts from one grade to another. In this research study, only children participating in testing bridges in Study Year Two (children enrolled in Grade 2 in Study Year One) would have encountered a classroom building context similar to the survey question and thus would be expected to show the greatest improvement over the course of the study. This was not supported by statistical analysis. Instead, Table 7 showed that when individual grades are examined, only children who were in Grades 3 and 4 in Study Year One showed a significant change in Study Year Three. In Study Year Two, children formerly in Grade 3 would have participated in the Building Devices and Vehicles That Move topic while children formerly in Grade 4 would have experienced the Mechanisms Using Electricity topic. Both of these program topics involve extensive experiences with constructing devices and performing fair tests but in contexts different from that displayed in the survey question. Future research on how particular contexts may or may not assist children to develop evaluating and testing skills over time would be useful. Other researchers have observed that some skills can be generalized to other contexts far better than others ( Ridgway & Passey, 1992 ). They have speculated that time taken to learn some skills, the degree to which a task may be contextualized, and the way in which each child has structured existing knowledge may all help account for variations in skill generalizability ( Ridgway & Passey, 1992 ). We would tend to agree with this more complex interpretation of skill generalizability while adding that in this research study, the issue was further complicated by the lack of professional support for teachers. This lack of support influenced teachers' understanding of the program and consequently affected the degree to which children could structure an understanding of program components. Results addressing study questions about age and gender differences are more difficult to interpret. Results show that in general, younger children responded to the survey question slightly differently from older children. In Study Years One and Three, younger children tended to provide ideas about testing that were in the first three categories. Older children showed a slightly greater inclination for more detailed answers. In regard to gender differences, results show that depending on the grade, either the boys or the girls could be judged as outperforming the other gender, but these distinctions were not greatly significant. We believe that study limitations can help account for these more indistinct results. One limitation would involve contextual variables associated with the survey question. Anning (1994) warned that contextual variables will affect children's responses and the type of question, the context of the question, support for reading the question, and children's previous experiences with bridges can affect their answers. Another limitation is the variability in Study Year Two experiences. If skill capability is influenced by context, teaching practice, and teacher preparedness, then the variety of learning contexts in which evaluating and testing were developed in Study Year Two might well have influenced study results. A third limitation might lie in using an atomized assessment to make judgements about children's capabilities. Kimbell (1992) cautions against the exclusive use of atomized assessments and advises that if atomized assessments are used, they should be balanced with whole judgements derived from children's performance on a variety of tasks. Study results, as well as limitations to this study, help reveal productive areas for future research. In order to assist with characterizing children's testing strategies for any one age group or gender, children could be observed as they participate in a number of similar contexts that involve testing or evaluating. In this way, a more extensive profile of testing strategies might emerge which could show more distinct trends in children's thinking. Information about children's thinking would help inform the design and content of school technology programs. Further, children could be observed as they participate in a number of different contexts; children's work in these contexts could then be compared in order to help answer in what ways context contributes to skill development. Information about contexts could influence the nature of practical activities recommended for inclusion in school programs and teachers' selection of classroom activities. Finally, the study could be repeated after teachers had gained more expertise with teaching design technology. Perhaps when teachers had the support and time to become familiar with technological problems solving, concepts and discourse, more insight could be gained into how participation in school technology programs influences children's skill development.
The support of this work HRC-Northern Telecom Grant #812950007 is gratefully acknowledged.
An earlier version of this paper was presented at the Annual Meeting of the National Association for Research in Science Teaching, Boston, MA, March 30, 1999.
References
Aikenhead, G. S. (1988) . An analysis of four ways of assessing student beliefs about STS topics. Journal of Research in Science Teaching, 25(8), 607-629.
Alberta Education. (1996) . Alberta elementary science program. Alberta: Alberta Education.
Appleton, K. (1997) . Teaching science: Exploring the issues. Queensland: Central Queensland University.
Anning, A. (1994) . Dilemmas and opportunities of a new curriculum: Design and technology with young children. International Journal of Technology and Design, 4, 155-177.
Anning, A. (1997) . Teaching and learning how to design in schools. Journal of Design and Technology Education, 2(1), 50-52
Anning, A., Jenkins, E., & Whitelaw, S. (1996) . Bodies of knowledge and design-based activities: A report to the Design Council. England: Design Council.
Bottrill, P. (1995) . Designing and learning in the elementary school. Washington: International Technology Education Association.
Coenen-Van Den Bergh, R. (Ed.). (1987) . Report PATT conference: Volume 2 Contributions. Netherlands: Bariet, Runinen.
Davies, D. (1996) . Professional design and primary children. International Journal of Technology and Design Education, 6(1), 45-59.
DES, (1992) . Technology: Key stages 1, 2 and 3: A report by the HMI Inspectorate on the second year, 1991-92. London: HMSO.
Department for Education and the Welsh Office (DFE/WO). (1995) . Design and technology in the National Curriculum. HMSO: London.
Driver, R. (1989) . The construction of scientific knowledge in classrooms. In R. Millar (Ed.), Doing science: Images of science in science education (pp. 83-106). London: Falmer.
Gadd, T., & Morton, D. (1992a) . Blueprints: Technology key stage 1. Cheltenham: Stanley Thornes.
Gadd, T., & Morton, D. (1992b) . Blueprints: Technology key stage 2. Cheltenham: Stanley Thornes.
Gustafson, Brenda J., Rowell, Patricia M., & Rose, Dawn P. (1999) . Elementary children's conceptions of structural stability: A three year study. Journal of Technology Education, 11(1), 26-42 .
Harlen, W., & Jelly, S. (1989) . Developing science in the primary classroom. Essex: Oliver & Boyd.
Harrison, P., & Ryan, C. (1990) . Folens technology in action. Dunstable: Kenley.
Johnsey, R. (1995) . The design process: does it exist? International Journal of Technology and Design Education, 5(3), 199-217.
Johnsey, R. (1997) . Improving children's performance in the procedures of design and technology. Journal of Design and Technology Education, 2(3), 201-207.
Kimbell, R. L. (1992) . Assessing technological capability. ICTE.
Kimbell, R., Stables, K., & Green, R. (1996), . Understanding practice in design and technology. Buckingham: Open University.
Layton, D. (1993) . Technology's challenge to science education. Philadelphia: Open University.
McCormick, R. (1996) . Conceptual and procedural knowledge. A paper presented at the Second Jerusalem International Science and Technology Conference on Technology Education for a Changing Future: Theory, Policy and Practice, Jerusalem, January 8-11, 1996.
McCormick, R., Murphy, P., & Hennessy, S. (1994) . Problem solving process in technology education: A pilot study. International Journal of Technology and Design Education, 4, 5-34.
McCormick, R., Murphy, P., Hennessy, S., & Davidson, M. (1996, April) . Problem solving in science and technology education. Paper presented at the American Educational Research Association Annual Meeting, New York, N. Y.
Osborne, R. J., & Freyberg, P. S. (1985) . Learning in science: The implications of children's science. Auckland: Heinemann.
Rennie, L. J. (1987) . Teachers' and pupils' perceptions of technology and the implications for curriculum. Research in Science and Technological Education, 5(2), 121-133.
Rennie, L. J., Treagust, D. F., & Kinnear, A. (1992) . An evaluation of curriculum materials for teaching technology as a design process. Research in Science and Technological Education, 10(2), 203-217.
Ridgway, J., & Passey, D. (1992) . Developing skills in technology: The theoretical bases for teaching. ICTE.
Roden, C. (1997) . Young children's problem solving in design and technology: towards a taxonomy of strategies. Journal of Design and Technology Education, 2(1), 14-19.
Ross, C., & Brown, N. (1993) . Girls as constructors in the early years. Stoke-on-Trent, UK: Trentham Books.
Rowell, Patricia M., & Gustafson, Brenda J. (Eds.). (1998) . Problem solving through technology: Case studies in Alberta elementary classrooms. University of Alberta: Centre for Mathematics, Science, and Technology Education.
Rowell, Patricia M., Gustafson, Brenda J., & Guilbert, Sandra M. (1999a) . Engineers in elementary classrooms: perceptions of learning to solve technological problems. Research in Science and Technological Education, 17(1), 109-118.
Rowell, Patricia M., Gustafson, Brenda J., & Guilbert, Sandra M. (1999b) . Characterization of technology within an elementary science program. International Journal of Technology and Design Education, 9, 37-55.
Symington, D. J. (1987) . Technology in the primary school curriculum: teacher ideas. Research in Science and Technological Education, 5(2), 167-172.
Tickle, L. (Ed.). (1990) . Design and technology in primary school classrooms. London: Falmer.
Williams, P., & Jinks, D. (1985) . Design and technology 5-12. London: Falmer.