JTE v28n1 - Advancing Diagnostic Skills for Technology and Engineering Undergraduates: A Summary of the Validation Data
Advancing Diagnostic Skills for Technology and Engineering Undergraduates: A Summary of the Validation Data
W. Tad Foster, A. Mehran Shahhosseini, & George Maughan
Abstract
Facilitating student growth and development in diagnosing and solving technical problems remains a challenge for technology and engineering educators. With funding from the National Science Foundation, this team of researchers developed a self-guided, computer-based instructional program to experiment with conceptual mapping as a treatment to improve undergraduate technology and engineering students' abilities to develop a plan of action when presented with real technical problems developed in collaboration with industrial partners. The pilot-testing and experimental portions of the project confirmed that the subjects found the training interesting and useful. However, the experimental data did not support the conclusion that the treatment caused an increase in diagnostic performance. Analysis of individual data demonstrated that for a portion of the sample, significant gains occurred. Qualitative analysis demonstrated that the majority of the students treated the experience as a trivial academic exercise, which seriously limited their efforts. A major step forward occurred in the ability to automatically compare student maps with the expert's reference map using a modified version of the similarity flooding algorithm. Student feedback was based on this automatic comparison. In all, the experience has encouraged the team to continue and expand the use of conceptual mapping as a tool for improving diagnostic and problem-solving skills.
Keywords: diagnostic skills; conceptual mapping; self-guided instructional design; similarity flooding
Introduction
For some time, technology and engineering educators have focused on improving students' cognitive and metacognitive abilities, especially in the areas of design and problem solving. It is clear that these abilities are essential for personal and professional success. However, an argument can be made that more work is needed. This study was an attempt, supported by funding from the National Science Foundation, to develop and pilot test computer-based, self-paced diagnostic skills training using conceptual mapping techniques developed by Novak (1977) . Cognitive abilities are highly successful predictors of job performance, and the development of advanced cognition skills is critical to perform any diagnostic assignment. According to Gabbert, Johnson, and Johnson (2001) , one of the ways to address cognitive development is "by examining the strategies students use to complete learning tasks" (p. 267). Causal-model theory argues "that, in principle, people are sensitive to causal directionality during learning"; our learning does not involve only "acquiring associations between cues and outcomes irrespective of their causal role" ( Waldmann, 2000, p. 53 ). It is predicted by associative theories that in some learning conditions, our representations are fundamentally flawed. There is
evidence that learning from experience seems more of a process of negotiation in which thinking, reflecting, experiencing and action are different aspects of the same process. It is negotiation with oneself and in collaboration with others that one may actually form the basis of learning. ( Brockman, 2004, p. 141 )
Interestingly, this applies as well to the informal learning that occurs in such technical situations as help desk support for information systems. Haggerty (2004) noted that the support and implementation of structured and systematic problem-solving processes and detailed verbal modeling of explanations about the problem are critical to the development of advanced cognition and effective outcomes because they will also increase self-efficacy and satisfaction.
Diagnostic learning (i.e., analyzing causes based on information about the effects) needs to be differentiated from predictive learning (i.e., determining effects based on specific causes). "An important feature of diagnostic inference is the necessity of taking into account alternative causes of the observed effect" ( Waldmann, 2000, p. 55 ). Given that the effects (symptoms) have already occurred and are not necessarily actively recognized by the learner, "diagnostic learning is a test case for humans' competency to form and update mental representation in the absence of direct stimulation" ( Waldmann, 2000, p. 73 ).
Some technical problems are well defined with a clear goal: There is a definite cause and outcome and a proven algorithm to ensure that the problem is solvable. However, many technical problems are ill-defined: The cause or causes, what constitutes relevant data, and the steps to be taken are unclear. Consequently, there is a need for advanced cognitive skills such as analytical, creative, and practical thinking when diagnosing technical problems. Writing from an organizational perspective, Okes (2010) states that a "problem is often not a single problem but many different problems" (p. 38). In such cases, the diagnosis will be difficult since there are likely to be multiple causes. The ability to diagnose multiple causes of a common effect versus a common cause for multi[ple] effects requires the technician to learn about these fundamental causal relationships correctly. And this ability is improved through practical experience and the ability to evaluate the causes and solutions of problems. Waldmann (2000) believes that a combination of technical expertise and logical and creative thought processes are essential for diagnosing a problem. Okes (2010) makes a distinction between creative problems and analytical problems: With creative problems, multiple solutions are necessary; however, analytical problems require "the right solutions [that] will not be known until a proper diagnosis is done. [For analytical problems,] it is the [utilization of a] diagnostic process, known as root cause analysis, which finds the causes" (p. 37).
Technical Diagnostic Work
"Most people never receive training in root cause analysis, and those who are experts have often learned it through years of experience diagnosing a wide range of problem situations" ( Okes, 2010, p. 36–37 ). One of the ways in which diagnostics skills are developed is through the understanding of cause and effect relationships when performing diagnostics. Typically, technical workers learn "cause and effect relationships resembling symptom–cause troubleshooting charts which they held in memory for use in subsequent troubleshooting" ( Green, 2006, Abstract, p. 2 ).
Troubleshooting requires the technician to utilize problem-solving skills. According to Sharit and Czaja (2000) , this is one of the most complex cognitive processes. Haggerty (2004) writes that providing "technical support [is] . . . one mechanism by which [information system] users can gain the necessary knowledge, skills and abilities to use their technology [the system] effectively" (p. iii). As Haggerty (2004) states, "effective support is characterized by a timely and well structured problem solving process where a knowledgeable, sympathetic and patient analyst provides thorough and specific information and explanations, matched to the user's demonstrated level of ability, according to the needs of the specific technical problem" (p. iii). Technical workers, however, often encounter complex, ill-structured problems in their professional efforts to solve technical problems and do not have access to any form of technical support. Three major issues relative to organizational culture's impact on problem solving are identified by Okes (2010) , including: how people view problems (e.g., someone to blame), who will be called upon to diagnose and solve the problem, and the ratio of the number of problems to the available personnel to solve them.
Instructional Techniques
Most would agree with Stoyanov and Kirschner (2007) that "solving problems is considered an important competence of students in higher education" (p. 49) and that higher education institutions must take on this important task. What seems to be at issue is how to go about the task effectively. Historically, problem-solving instruction has focused mostly on well-defined problems and a rather simple, step-by-step approach. However, most situations that are viewed as problems are typically not well defined, nor do people tend to be successful in solving them using a simplistic problem solving heuristic. What seems to be needed is practice with ill-defined problems within a supportive and instructional environment ( Stoyanov & Kirschner, 2007 ).
To develop diagnostic skills, "the knowledge that one should analyze the problem situation, generate ideas, select the most appropriate, and then implement and evaluate is necessary, but not sufficient" ( Stoyanov & Kirschner, 2007, p. 50 ). It is also important to know how to process information, form and test hypotheses, and make choices based on the data ( Johnson, 1994 ). "The selection and application of these procedures, techniques, and tools depends to a large extent on the desired outcomes of problem-solving determined by the nature of ill-structured problems and the cognitive structures and processes involved in solving them" ( Stoyanov & Kirschner, 2007, p. 50 ). "Instructional design should determine the most effective and efficient conditions of providing both process and operational support to solving ill-structured problems" (p. 50).
Writing on the topic of professional development, Mayer (2002) defines problem-based training as providing "realistic problems and the solutions of these problems in a variety of situations" (p. 263). He lists the four types of problem-based approaches enumerated by Lohman (2002) that "can be presented in computer-based environments, book-based environments, or live environments" ( Mayer, 2002, pp. 263–264 ): (1) case study , (2) goal-based scenario , (3) problem-based learning , and (4) action learning (p. 264). He theorizes that
"there are three cognitive steps in problem solving by analogy: (1) recognizing that a target problem is like a source problem you already learned to solve, (2) abstracting a general solution method, and (3) mapping the solution method back onto the target problem" (p. 267).
More research is needed "to understand how each of the problem-based training methods [in Lohman's (2002) article] supports the processes described [the three cognitive steps]" ( Mayer, 2002, p. 267 ). The use of graphical structures to help make sense of information is important to problem solving and systems thinking.
Novak, the person credited with the development of conceptual mapping, argues " that the central purpose of education is to empower learners to take charge of their own meaning making " ( Novak, 2010, p. 13 ). His work in conceptual mapping is based on the theoretical work of Ausubel, Piaget, and Vygotsky. Initially developed as a means to collect data about children's knowledge, his research quickly led to the conclusion that concept mapping was useful in helping students learn and helping teachers to organize instruction. It has also been demonstrated to be a useful tool for evaluating what has been learned. Recently, he has applied mapping as planning and problem solving in corporate settings.
Siau and Tan (2006) identify "three popular cognitive mapping techniques—causal mapping, semantic mapping, and concept mapping" (p. 96). The term cognitive map is developed in psychology as a means of describing an individual's internal mental representation of the concepts and relations among concepts. Cognitive mapping techniques are used in identifying subjective beliefs and to represent these beliefs externally. "The general approach is to extract subjective statements from individuals, within specific problem domains, about meaningful concepts and relations among these concepts and then to describe these concepts and relations in some kind of diagrammatical layout [Swan, 1997]" ( Siau & Tan, 2006, p. 100 ). This internal mental representation is used to understand the environment and make decisions accordingly. " Causal mapping [emphasis added] is the most commonly used cognitive mapping technique by researchers when investigating the cognition of decision-makers in organizations [Swan, 1997]" ( Siau & Tan, 2006, p. 100 ) because it allows an individual to interpret the environment with salient constructs. The theory argues that individuals, with their own personal system of constructs, use it to understand and interpret events. " Semantic mapping [emphasis added], also known as idea mapping, is used to explore an idea without the constraints of a superimposed structure [Buzan, 1993]" ( Siau & Tan, 2006, p. 101 ). With semantic maps, an individual will begin at the center of the paper with the principal idea and work outwards in all directions. This produces an expanding and organized structure consisting of key words and key images. Concept mapping is another cognitive mapping technique, which "is a graphical representation where nodes represent concepts, and links represent the relationships between concepts" ( Siau & Tan, 2006, p. 101 ). Concept mapping is an integral part of systems thinking.
Systems Thinking
Batra, Kaushik, & Kalia (2010) define systems thinking as
a holistic way of thinking, fundamentally different from that of traditional forms of analysis in which the observer considers himself the part of reality as a whole system. System[s] thinking resists the breaking down of problems into its component parts for detailed examination and focuses on how the thing being studied interacts with the other constituents of the system. . . . This means that instead of taking smaller and smaller parts or view[s] of the system taken for study, it actually works by expanding its view by taking into account larger and larger numbers of views or parts of the system. (p. 6)
"Systems thinking is increasingly being regarded as a 'new way of thinking' to understand and manage the 'natural' and 'human' systems associated with complex problems . . . (Bosch et al., 2007a)" ( Nguyen, Bosch, & Maani, 2011 ). When employing systems thinking to deal with real problems, it is necessary for the trainer to classify real-world problems by system language because the classification can help students or trainees find an appropriate method and methodology to deal with specific problematic situations. According to Batra et al. (2010) ,
The character / nature / approach of systems thinking makes it extremely effective on the most difficult types of problems to solve. . . . Some of the examples in which system thinking has proven its value include: complex problems that involve helping many actors [learners] see the "big picture" and not just their part; recurring problems or those that have been made worse by past attempts to fix them; issues where an action affects (or is affected by) the environment surrounding the issue, either the natural environment or the competitive environment; and problems whose solutions are not obvious. (p. 6)
Batra et al. (2010) discovered that systems thinking leads to: "in-depth search of problem contributors by finding out further reasons for those problems and lead to actual reasons of the same," "solution[s] to all kinds of problems by considering them as a whole system" (p. 10), finding the root-cause of a problem by exploring not just analyzing the problem and making assumptions, and "permanent solutions of problems by acting on all possible reasons simultaneously [instead of just making] plans to solve the problem by removing the reasons one by one as per the plan formation" (p. 11).
Evaluation of Diagnostic Skills
In order to acquire skills, learning has to take place. According to Kontogiannis and Maoustakis (2002) , "most research in artificial intelligence and machine learning has . . . underplayed issues of problem formulation, data collection and inspection of the derived knowledge structures (Langley and Simon 1995)" (p. 117). They further state that the stages of inspection and evaluation of knowledge structures are significant because "by making knowledge structures easier to understand or comprehend, we are in a better position to meet criteria of validation, generalization and discovery." (p. 133). Basically, the issue of comprehensibility must be part of the evaluation process for technical applications. The learner has to be able to input and output knowledge. Comprehensibility should address transferability to a new context in the future. With the increased use of computer-based diagnostic skills, evaluation is not done separately from the ability of humans to interact with the computer to perform problem-solving tasks.
Kontogiannis' and Maoustakis' (2002) "informal approach for refining and elaborating knowledge structures" (p. 120, Figure 1) provides some insight on what to consider when performing evaluations of diagnostic skills. The model illustrates the significance of the individual to become an expert in the field to effectively perform diagnostics. It is imperative that the expert is able to employ several diagnostic strategies. This entails "fault-finding strategies and knowledge structures [, which] are dependent upon the amount and kind of data that are available—for example, data regarding equipment reliability data, direction and rate of change of process variables, sequences of change, etc." (p. 120). Their model demonstrates the significance of identifying any weakness in the process at the analytical stage. The role of the expert is to determine if the process for solving the problem was justifiable in terms of the principles of operation. At the modification stage, the ability of the learner "to impose a hierarchical structure upon the" (p. 123) process is crucial to problem solving. This would entail "providing descriptions of groups of faults that relate functionally to each other" (p. 123). Moreover, the creation of subordinate goals and plans are important as they are "high-level objectives or concepts . . . . By progressively breaking up all goals into plans or sequences of checks, the overall task becomes easier to achieve" ( Kontogiannis & Maoustakis, 2002, p. 123 ). Kontogiannis and Maoustakis further explain that "the distance or gap between the top goal and the available responses [, verbal statements of the problem made at a high or detailed level,] becomes smaller" (p. 123). The subjects of their study were required to participate in fault-finding activities. This demonstrated the level to which they were able to transfer what was learned. In order to study subjects' diagnostic skills, the authors created three modules: "Module 1—Training," "Module 2—Fault finding test in the manual mode" (p. 128), and "Module 3—Transfer to diagnosis in the automatics mode" (p. 129). Their findings indicated "that deep goal structures facilitate both the acquisition and the transfer of knowledge" (p. 132).
Problem and Purpose of the Study
Research to date supports the assertion that domain-specific problem-solving skills can be developed by educational and training programs. The more experience an individual has with a system and with solving problems that occur in the system, the more proficient a problem solver that individual becomes. What is less certain is the extent to which general problem-solving instruction can result in improvements in near and far transfer of knowledge to novel problem situations. There is strong evidence that the application of conceptual mapping improves learning, memory, and application of knowledge. It is also clear that conceptual mapping enhances systemic understandings.
This project was designed to test the premise that the use of conceptual mapping techniques to force in-depth analysis of technical problems and the creation of a process map of the student's intentions during the diagnosis phase of problem solving would increase the student's level of accuracy when compared to the process used by experts in the particular system. It was argued that developing this expertise in mapping would help the students become more agile in their thinking regarding ill-defined problems.
A quasi-experimental model was used to test the null hypothesis H 0 : μ Δ1 = μ Δ2 = μ Δ3 = μ Δ4 . In other words, there would be no statistically significant difference between the four groups in terms of the mean difference in percentage accuracy for the two trials.
Method
The project staff developed a 2-hour, computer-based training program using the Lectora authoring software. The first hour of this training was designed to introduce students to systems and troubleshooting problems. During this phase of the training, the subjects were taught to use the Visual Understanding Environment (VUE) open-source software to develop conceptual and process maps. Also during this phase, the subjects were given a "simple" technical problem and asked to map out a plan of action. Using a similarity flooding algorithm, the students' maps was then electronically compared to an expert's map that was already encoded. The information developed by the algorithm was returned to the subjects as feedback so that they would know how well they did.
The second phase of the training took the form of two technical problems developed in collaboration with industrial partners. The first problem involved an electrical grid distribution system, and the second problem focused on a malfunctioning heat exchanger system. In both cases, the subjects were provided with a description of the system and tables containing operational information. From the information presented, the subjects were asked to analyze the system and develop a process map for addressing the apparent malfunction.
The evaluation of this project included pilot-testing the training program after the completion of the first hour, after the completion of the electrical grid problem, and after completion of the full training program. The subjects were provided the program and all necessary software on a memory stick and typically completed the training on a laptop.
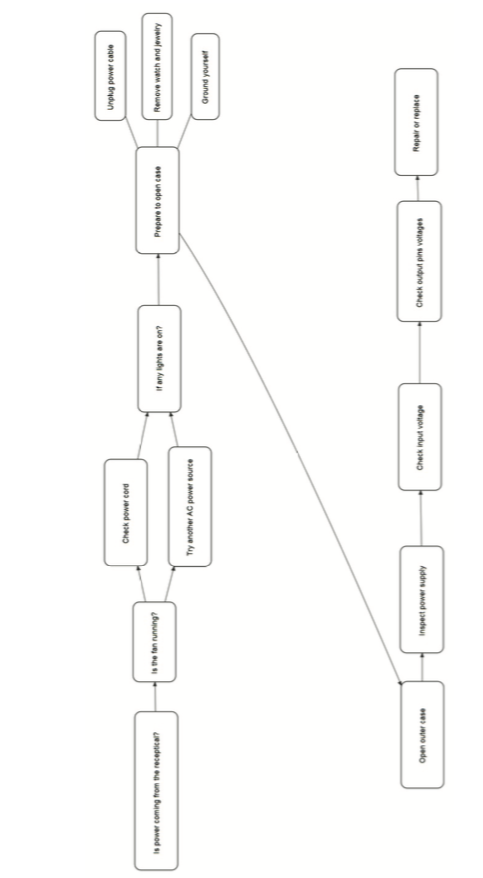 Figure 1.
Sample expert process map (practice problem).
Figure 1.
Sample expert process map (practice problem).
Instrumentation
A feedback questionnaire was developed to provide subjects the opportunity to express their reactions to the training. The Likert-type questions were similar to end-of-course student evaluations of instruction. In this case, the focus was on the "look and feel" of the program and the extent to which the students perceived the training to be interesting, relevant, and helpful. Subjects were also encouraged to provide open-ended comments.
Population and Sample
The population for this study was junior and senior undergraduates enrolled in engineering, engineering technology, and closely related majors. The sample was drawn from students enrolled in the College of Technology at Indiana State University (the Principle Investigators' home institution) and four other universities. Faculty members involved with Indiana State University's PhD in Technology Management Consortium and faculty members at the four other institutions accepted invitations to participate. The sample consisted of the classes of those faculty members.
There were four treatments, and the groups were randomized and assigned to the groups of students in the order in which the faculty of these groups agreed to participate. Typically, faculty members would volunteer a particular class that they taught because the training was perceived to be relevant to the focus of the particular course. Subject participation was voluntary, confidential, and anonymous.
Data Collection
Experimental data was collected automatically as the subjects completed the training. The primary dependent variable for the experiment was the difference in percent accuracy for the two attempts for each problem. Upon completion and submission of the subject's map, the map was compared to the expert's map, and percentage accuracy was reported. The subject received this percentage as feedback. One group only received its scores (control condition). The other three groups were given a secondary form of additional feedback: metacognitive cues, review of the expert map, and both. All subjects then were given the opportunity to revise and resubmit their maps. The resubmission was also evaluated for accuracy, and the percentage was reported to the students and recorded.
After completing the training program, the subjects were given a "satisfaction" questionnaire to provide feedback regarding their reactions to the training. There was a range of 1–4 for each of the eight questions asked. Consequently, the overall range for the satisfaction score was 8 to 32 points.
Data Analysis
Student satisfaction data was analyzed using only descriptive statistics that resulted in a mean and standard deviation for each question and the total for all eight questions (i.e., overall satisfaction). Experimental data analysis included testing the differences in percentage accuracy between the first draft and second draft of the subject's process maps. In addition, one-way analysis of variance was used to determine if there were any differences in mean percentage accuracy based on treatment type, university where the subject was studying, and major.
Results
Sample
A total of 130 subjects participated in the experimental portion of this project. Table 1 provides a summary of the demographic data collected.
| Gender | Major | University | |||
|---|---|---|---|---|---|
| Female | 9 (7%) | Mech. Eng. Tech. | 58 (44.6%) | ISU | 72 (55.4%) |
| Male | 106 (81.5%) | Const. Mgmt. | 35 (26.9) | BGSU | 35 (26.9%) |
| NR | 15 (11.5%) | Info. Tech. | 15 (11.5%) | IUPUI | 11 (8.5%) |
| Mech. Eng. | 11 (8.5%) | PU | 8 (6.1%) | ||
| Pack. Tech. | 10 (7.7%) | RHIT | 4 (3.1%) | ||
| Elec. & Comp. Tech | 1 (.8%) | ||||
The home institution for this project was Indiana State University. As a result, the majority (55.4%) of the subjects were from that university. Subjects enrolled in mechanical engineering (8.5%) and mechanical engineering technology (44.6%) comprised 53.1% of the total. The majority (81.5%) of the subjects were male.
Satisfaction
Overall, on a scale of 8–32 points, the mean score for subject satisfaction with the training was 25.62 (S n-1 = 3.25). Each subject's ratings were averaged across the eight questions. The overall mean for all subjects was 3.2. Table 2 provides a summary for each of the eight questions.
| Item | M | SD |
|---|---|---|
| 1. The computer based training was interesting | 3.09 | 0.67 |
| 2. The screen design was reasonably attractive | 3.15 | 0.55 |
| 3. The screen layout was logical (i.e., made sense) | 3.27 | 0.57 |
| 4. All of the program buttons worked as expected | 3.21 | 0.70 |
| 5. It was easy to navigate my way through the program | 3.29 | 0.66 |
| 6. The content of the training program was meaningful | 3.12 | 0.64 |
| 7. This training would be useful to anyone in a technical career | 3.27 | 0.67 |
| 8. Overall, this was a high quality, professional experience | 3.22 | 0.6 |
Of the 126 subjects to complete the satisfaction inventory, only 28 (22%) had an overall mean satisfaction rating below 3.0. The mean satisfaction scores ranged from a low of 1.75 (one subject) to a high of 4.0 (four subject).
The majority of the subjects chose not to provide any written comments. Of the 26 subjects who did comment, 11 (42%) made positive comments, and 15 (58%) made negative comments. The negative comments focused on parts of the program that did not work as expected and on needing more time to complete the training. One participant thought that the training would be stronger if it were more challenging.
Experimental Validation
Subjects were offered the opportunity to provide a process map for three problems during the training. The first problem was used as an orientation to the process that they would be using for the two main problems. For the first problem, the subjects were only given the opportunity to provide one map. Based on a comparison with the expert's map for that problem, the overall mean was 18% accuracy (S n-1 = .16). In other words, the subjects found the task somewhat challenging.
Taken as a whole, the subjects who completed the second problem (i.e., electrical power grid problem) scored an average of 18.8% (S n-1 = .042) on their first submission and 15.4% (S n-1 = .043) on their second attempt. A paired samples t-test revealed that the difference was statistically significant (t (129) = 2.919, p < .01), although the reverse of expectations. Subjects who completed the third problem (i.e., heat exchanger problem) scored on average 11.7% (S n-1 = .021) for their first submission and 12.6% (Sn-1 = .03) for their second submission. This was not found to be a statistically significant difference (t (128) = -1.17, p > .05). In all cases, percent accuracy was based on 100% (i.e., perfect match).
| Diff_1 | Diff_2 | ||||
|---|---|---|---|---|---|
| Group | n | M | SD | M | SD |
| 1 | 35 | -.06214 | .176141 | -.00243 | .014368 |
| 2 | 32 | -.00813 | .123798 | .04019 | .129542 |
| 3 | 35 | -.02497 | .088989 | -.01091 | .101700 |
| 4 | 28 | -.03775 | .117151 | .00764 | .026403 |
| Total | 130 | -.03358 | .131248 | .00795 | .085689 |
The null hypothesis was that the mean difference for the three treatments would be equal to one another and the control group. Based on a one-way analysis of variance, the null hypothesis could not be rejected for the electrical grid problem ( F (3, 126) = 1.014, p = .389) nor for the heat exchanger problem ( F (3, 126) = 2.315, p = .079). As can be seen, the mean difference for the two submissions for the heat exchanger problem was most pronounced. In addition, no statistically significant differences were found based on gender, major, or the university at which the students were studying.
Although group data confirmed that by and large the subjects did not perform well on the three problems included in this training, analysis of the top performing subjects demonstrated that some students did in fact understand the problem and the process mapping technique reasonably well, as shown in Table 4.
| Electric Grid Problem | Heat Exchanger Problem | ||
|---|---|---|---|
| First Attempt | Second Attempt | First Attempt | Second Attempt |
| 0.560 | 0.734 | 0.651 | 0.535 |
| 0.461 | 0.526 | 0.497 | 0.692 |
| 0.423 | 0.652 | 0.491 | 0.554 |
| 0.515 | 0.751 | 0.419 | 0.537 |
| 0.493 | 0.741 | 0.475 | 0.648 |
| 0.342 | 0.829 |
Discussion
As stated earlier, the purpose of this project was to experiment with the development of a self-paced, computer-based program (using the Lectora authoring software) to introduce engineering and technology undergraduates to conceptual mapping techniques to help enhance their diagnostic skills for technical problems. The first hour of this training was designed to introduce students to systems and diagnosing problems. This phase covered the use of the Visual Understanding Environment software to develop conceptual and process maps. Also during this phase, the subjects were given a "simple" technical problem and asked to map a plan of action. Using a similarity flooding algorithm, the students' maps were then electronically compared to an expert's map that was already encoded. The information developed by the algorithm was returned to the subjects as feedback. The second phase of the program included two technical problems developed in collaboration with industrial partners. The first problem involved an electrical grid distribution system, and the second problem focused on a malfunctioning heat exchanger system. In both cases, the subjects were provided with a description of the system and tables containing operational information. From the information presented, the subjects were asked to analyze the system and develop a process map for addressing the apparent malfunction.
The computer program was pilot-tested after completion of the first hour, after completion of the electrical grid problem, and after completion of the full training program. During the quasi-experimental phase, the subjects were asked to complete a satisfaction survey of the finished product and the overall experience. The quasi-experiment involved subjects from five universities and six majors in engineering or technology. The subjects were provided the program and all necessary software on a memory stick and typically completed the training on a laptop.
In short, the subjects during pilot testing and during experimentation found the training to be interesting (X̄= 3.09 on a 4-point scale) and useful (X̄ = 3.22 on a 4-point scale). However, on average, the subjects' level of performance was much lower than expected. It was clear that about 20% of the subjects clearly understood and found the mapping technique and the feedback provided to help them improve their diagnostic skills. In general, this was not the case. That is, performance on the two main tasks was low and remained low, regardless of the type of feedback given.
There were several indications that provide some explanation (i.e., limitations of the work to date). Qualitatively, all of the staff noted that during testing, the majority of the subjects (a) did not have enough time to complete both of the major problem-solving tasks and (b) were treating the exercise as any other academic exercise. A good number of the subjects did nothing more than complete a single map for the problem and simply resubmitted it after reading the feedback.
The data, feedback from the subjects, and researcher observations revealed that the electric grid problem was difficult for students to process. In other words, the heat exchanger problem was much more compatible with the simulation capabilities of the training program. Students tended to get lost in the screens provided as a static simulation of the electric grid.
Finally, it was clear that at least 2 hours were needed to complete the training as designed. In most cases, the exercise was fitted into a regular class period (75–90 minutes), typically without the professor in attendance. For most, it was not enough time to complete the training and the two problems.
A major contribution of this work was the development of automatic student feedback by programming the software using a similarity flooding algorithm ( Melnik, Garcia-Molina, & Rahm, 2002 ). This algorithm provides a means of comparing two graphic items such as conceptual maps. The project team modified the original algorithm to include an automatic thesaurus for synonyms, the use of relative similarity versus full similarity, weighting the nodes, and setting threshold values. Each modification significantly improved the algorithm's accuracy, so that it was possible to compare various expert maps with themselves and get a 100% matching indication. The team validated the algorithm using multiple tests (see Shahhosseini, Ye, Maughan, & Foster, 2014 , for a complete report of this work).
Technology and engineering educators at all levels are seeking additional ways to help students improve their cognitive and metacognitive reasoning skills. This project was an attempt to determine the extent to which a self-paced, computer-based program would help novice troubleshooters (i.e., students) learn important principles about mapping and diagnostics. The students found the training interesting and useful, but additional work is needed to ensure that the instruction is taken seriously by students. Further, the researchers will work to expand the work to all stages in the process from problem identification to solution and follow-up assessment.
Partial support for this work was provided by the National Science Foundation's Transforming Undergraduate Education in Science, Technology, Engineering, and Mathematics (TUES) program under Grant No. 1140677. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
W. Tad Foster ( tad.foster@indstate.edu ) is Professor in the Department of Human Resource Development and Performance Technology at Indiana State University; A. Mehran Shahhosseini ( Mehran.Shahhosseini@indstate.edu ) is Associate Professor in the Department of Applied Engineering and Technology Management at Indiana State University; George Maughan is Professor Emeritus in the Department of Human Resource Development and Performance Technology at Indiana State University.
References
Batra, A., Kaushik, P., & Kalia, L. (2010). System thinking: Strategic planning. SCMS Journal of Indian Management , 7(4), 5–12. Retrieved from http://www.scmsgroup.org/scmsjim/pdf/2010/SCMS%20Journal%20October-December%202010.pdf
Brockman, J. L. (2004). Problem solving of machine operators within the context of everyday work: Learning through relationship and community (Doctoral dissertation). Available from ProQuest Dissertations and Theses database. (UMI No. 3129464)
Gabbert, B., Johnson, D. W., & Johnson, R. T. (2001). Cooperative learning, group-to-individual transfer, process gain, and the acquisition of cognitive reasoning strategy. The Journal of Psychology: Interdisciplinary and Applied, 120 (3). 265–278. doi:10.1080/00223980.1986.10545253
Green, D. F. H. (2006). How refrigeration, heating, ventilation, and air conditioning service technicians learn from troubleshooting (Doctoral dissertation). Available from ProQuest Dissertations and Theses database. (UMI No. 3236882)
Haggerty, N. (2004). Towards an understanding of post-training user learning through IT support (Doctoral thesis). Available from ProQuest Dissertations and Theses database. (UMI No. NQ96823)
Johnson, S. D. (1994). Research on problem solving instruction: What works, what doesn't? The Technology Teacher, 53 (8) 27–29.
Kontogiannis, T., & Maoustakis,V. (2002). An experimental evaluation of comprehensibility aspects of knowledge structures derived through induction techniques: A case study of industrial fault diagnosis. Behaviour & Information Technology, 21 (2),117-135. doi:10.1080/01449290210146728
Lohman, M. C. (2002). Cultivating problem-solving skills through problem-based approaches to professional development. Human Resource Development Quarterly, 13 (3), 243–261. doi:10.1002/hrdq.1029
Melnik, S., Garcia-Molina, H., & Rahm, E. (2002). Similarity flooding: A versatile graph matching algorithm and its application to schema matching. In Proceedings of the 18th International Conference on Data Engineering (pp. 117–128). New York, NY: Institute of Electrical and Electronics Engineers. doi:10.1109/ICDE.2002.994702
Novak, J. D. (1977). A theory of education . Ithaca, NY: Cornell University Press.
Novak, J. D. (2010). Learning, creating, and using knowledge: Concept maps as facilitative tools in schools and corporations (2nd ed.). New York, NY: Routledge.
Nguyen, N. C., Bosch, O. J. H., & Maani, K. E. (2011). Creating "learning laboratories" for sustainable development in biospheres: A systems thinking approach. Systems Research and Behavioral Science, 28 (1), 51–62. doi:10.1002/sres.1044
Mayer, R. E. (2002). Invited reaction: Cultivating problem-solving skills through problem-based approaches to professional development. Human Resource Development Quarterly, 13 (3), 263–269. doi:10.1002/hrdq.1030
Okes, D. (2010, September). Common problems with basic problem solving. Quality Magazine, 49 (9), 36–40.
Sharit, J., & Czaja, S. J. (1999). Performance of a computer-based troubleshooting task in the banking industry: Examining the effects of age, task experience, and cognitive abilities. International Journal of Cognitive Ergonomics, 3 (1), 1–22. doi:10.1207/s15327566ijce0301_1
Shahhosseini, A. M., Ye, H., Maughan, G., & Foster, W. T. (2014). Implementation of similarity flooding algorithm to solve engineering problems using diagnostic skills training technique. In ASME 2014 International Mechanical Engineering Congress and Exposition. Volume 5: Education and Globalization. New York, NY: American Society of Mechanical Engineers. doi:10.1115/IMECE2014-39698
Siau, K., & Tan, X. (2006) . Cognitive mapping techniques for user–database interaction. IEEE Transactions on Professional Communication, 49(2), 96–108. doi:10.1109/TPC.2006.875074
Stoyanov, S., & Kirschner, P. (2007). Effect of problem solving support and cognitive styles on idea generation: Implications for technology-enhanced learning. Journal of Research on Technology in Education, 40 (1), 49–63. doi:10.1080/15391523.2007.10782496
Waldmann, M. R. (2000). Competition among causes but not effects in predictive and diagnostic learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 26 (1), 53–76. doi:10.1037/0278-7393.26.1.53