JVER v26n1 - Constructing Vocational and Technical College Student Persistence Models
Constructing Vocational and Technical College Student Persistence Models
Sea-Shon Chen
Dahan Institute of Technology, Taiwan, R.O.C.Hollie Thomas
Florida State UniversityAbstract
We constructed student persistence models for students at a vocational and technical college in Taiwan to predict student retention. Based on suicide, employee turnover, and social bond theories and relevant empirical research, a conceptual model was presented. Logistic regressions produced first and second semester persistence models. Our results also supported the statistical significance of nine variables (first semester GPA, entrance examination scores, gender, first semester social integration, second semester GPA, first semester gym grade, housing, major department, and occupational guidance program) in the conceptual model. The overall classification rate for the primary persistence model was 77.0%, and for the secondary persistence model, was 78.0%. The primary and secondary persistence models can be used to calculate the probability of persistence for freshman-year students at the end of the first and second semesters.
The problem of dropouts in Taiwan is similar to that in U.S. colleges and technical schools. The problem has been documented in the U.S. as early as 1880 ( Tinto, 1982 ). However, little is known about the predictors of persistence/dropout in Taiwan. In community colleges in the U.S., "Only a third of all beginning full-time students earn associate degrees" ( Tinto, Russo, & Kadel, 1994, p. 26 ). Many variables could account for the substantial dropout rate of vocational-technical students, e.g., high school GPA, socioeconomic status, SAT or ACT scores, gender, departments, housing, financial aid (e.g., Eaton & Bean, 1995 ; Metzner, 1989 ; St. John & Starkey, 1996 ; Webb, 1988 ). While this problem has been studied extensively in the U.S., little is known about persistence in vocational technical schools in Taiwan. This research is an attempt to determine whether models developed in the U.S. are generalizable to other cultures such as that of Taiwan. In addition, it was thought desirable to identify factors that contribute to persistence/dropout so that the college could assist those students whose life goals would be met by persisting in their selected curricula.
Because of differences between four-year colleges or universities and two-year or vocational-technical colleges, available predictors of persistence or retention for students enrolled at these two types of institutions may differ. No report is available that includes all suitable variables to form a prediction model of two-year or four-year college student persistence. Thus, we sought to identify important variables that could be used to construct models of five-year vocational-technical college student persistence in Taiwan. Models of student persistence would be useful as reference models for identifying students who are on the verge of dropping out. We sought answers to these questions: What are pragmatic and significant variables that affect five-year vocational-technical college student persistence? Can prediction models of college student persistence be developed? It is anticipated that the answers to these questions in the culture of Taiwan will provide assistance to student advisors as well as provide input to researchers within and without Taiwan as to how models of persistence may be revised.
We held two assumptions at the outset of this study. First, students are able to make the decision to stay in or drop out of school. Second, we believed that students' records in the college offices were correct. In the following section, articles are reviewed, and a suggested model for empirical study is described.
Review of Literature
College student persistence models that were developed since 1970 were reviewed first. Critical analyses (i.e., comparing and synthesizing the literature) were performed to identify relevant variables and select an appropriate statistical method. Finally, we suggest a conceptual model that could be used for this study. In the following, we specify and integrate literature on concepts or issues to be studied.
Available Models
Spady ( 1970 ), based on Durkheim's suicide model, suggested a sociological model of the dropout process. Spady found suicide and dropping out of a selected course of action, matriculation in school in this case, to have many parallels in that both involve the termination of a course of action. In 1971, Spady used multiple regression analysis to form the empirical models and found six statistically significant predictors (academic integration, social integration, socioeconomic status, gender, choice of department, and SAT/ACT).
Pascarella and Terenzini ( 1979 ) synthesized Spady's ( 1970 ) model, Spady's ( 1971 ) empirical models, and Tinto's ( 1975 ) model to study college dropouts. Two-group discriminant analysis was the statistical tool. They found three variables (academic integration, social integration, and gender) significantly related to persistence. Bean ( 1989 ) also identified these three variables when, based upon Price's ( 1977 ) model of employee turnover, he proposed a conceptual model and used path analysis to study student attrition.
Pascarella and Terenzini ( 1983 ), Pascarella and Chapman ( 1983 ), Stage ( 1988 ), and Stage ( 1989 ) all used Tinto's ( 1975 ) model to conduct analyses to predict first-year student persistence. The important variables of precollege performance, ethnicity, and dormitory were recognized, in addition to the former significant predictors of academic integration, social integration, and gender.
Webb ( 1988 ) combined Spady's ( 1970 ), Tinto's ( 1975 ), Pascarella's ( 1980 ), Bean and Metzner's ( 1985 ) models, and Bean's ( 1986 ) metamodel of continued enrollment to conduct the research. A step-wise multiple regression analysis with 28 predictors was used to analyze the record of 15,132 students. In Webb's paper, we found the vocational education program to be the tenth significant variable.
Metzner ( 1989 ) used Bean and Metzner's ( 1985 ) theoretical model with multiple regression to study the freshman attrition. Cabrera, Stampen, and Hansen ( 1990 ) introduced human capital theory ( Becker, 1964 ) and hypothesized a conceptual model to study student persistence. Nora, Attinasi, and Matonak ( 1990 ) adapted Tinto's ( 1975 ) theoretical model to form their conceptual model and conduct path analysis to predict student persistence. Ethington ( 1990 ) assumed a psychological model of student persistence and conducted empirical study. Stage and Rushin ( 1993 ) proposed a model of student predispositions to college and persistence in college and used LISREL to estimate relationships among the variables within the causal model. Cabrera, Nora, and Castaneda ( 1993 ) combined Tinto's ( 1975 ) model and Bean's ( 1986 ) model to create a structural equation model and used LISREL VII to construct a two-step structural model. Eaton and Bean ( 1995 ) used the psychological approach behavioral theory to develop a conceptual model and studied the retention with multiple regression, LISREL, and logistic regression. St. John and Starkey ( 1996 ) examined the influence of student financial aid on within-year persistence and used logistic regression to analyze data. In these papers, statistically significant variables were academic integration, social integration, socioeconomic status, gender, precollege performance, ethnicity, and price. Price was the eleventh important variable that we identified. In the following paragraph we have summarized significant variables and models.
Significant Independent Variables
Eleven statistically significant variables were found in the literature review. The variables of academic integration, social integration, socioeconomic status, gender, and precollege performance strongly influenced persistence. Major departments, ethnicity, SAT/ACT scores, living in a dormitory, vocational education program status, and price also influenced persistence.
Conceptual and Empirical Models
The literature revealed many models (e.g., Bean & Metzner, 1985 ; Cabrera, et al., 1990 ; Cabrera, et al., 1993 ; Eaton & Bean, 1995 ; Nora, et al., 1990 ; Spady, 1970 ; Stage & Rushin, 1993 ; St. John & Starkey, 1996 ; Tinto, 1975 ; Webb, 1988 ) that have been used to explore college student persistence. In the 1970s and 1980s, researchers tended to use Tinto's ( 1975 ) conceptual model. Up to the 1990s, researchers proposed their own conceptual models and formed new empirical models. We also found from the study and the literature that: (a) the females and males have different significant predictors and model structures (e.g., Bean, 1980 ; Spady, 1971 ); (b) the resulting models were different because two- or four-year college and vocational or nonvocational education program status were not the same, (e.g., Stage, 1988 ; Webb, 1988 ); (c) background variables directly influenced persistence in the model as was found in studies conducted by Webb ( 1988 ), Stage ( 1989 ), Cabrera et al., ( 1990 ), Ethington ( 1990 ), Stage and Rushin ( 1993 ), and Eaton and Bean ( 1995 ); and (d) some significant psychological variables, e.g., value, personality, and satisfaction could be employed to improve the model (e.g., Eaton & Bean, 1995 ; Ethington, 1990 ). Based upon the 11 important variables recognized and the examination of models, we propose and discuss a new model.
Conceptual Model Proposed
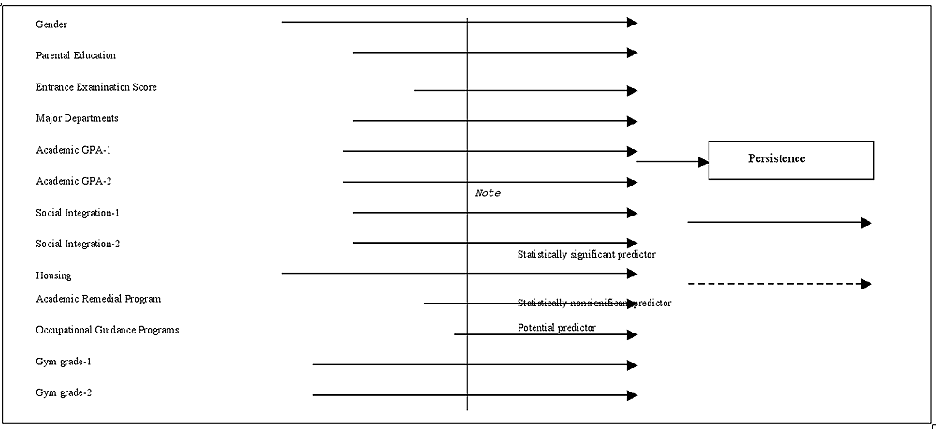
We used the significant variables identified and added predictors of academic remedial program, occupational guidance program, and gym grades to form a conceptual model (See Figure 1 ). Variables used to construct the conceptual model are specified and discussed next.
Academic integration . This variable is basically grade performance. Corresponding to suicide and turnover theories, students with low grades may be dissatisfied and lose their confidence, thus they may decide to drop out. Academic integration was a significant predictor in 13 studies.
Social integration . This concerns students' leadership and campus activities. In Taiwan, advisors give this score to each student in judging their own leadership, participation in extra-curricular activities, and the student's discipline when he/she is in school. Corresponding to suicide and turnover theories, students who join campus activities may feel that they belong and fit in the college; thus, they will persist in the college. Social integration was a significant predictor in 10 studies.
Parental education . Parental education is a major variable of socioeconomic status (SES) and correlates to the price variable (e.g., Cabrera, et al., 1993 ; St. John & Starkey, 1996 ). Corresponding to human capital theory, parents' education levels are correlated with student's persistence, because the student is able to pay the tuition and expense. SES was reported as a significant predictor in nine studies.
Gender . Authors of nine articles reported that gender was a significant variable of persistence. The predictive validity in gender difference was also found in these studies.
Entrance examination . Aptitude is a variable measured by the SAT/ACT and is similar to precollege performance. Like SAT/ACT scores, entrance examination scores are used to assess students' precollege performances and used to meet entrance examination requirements in Taiwan. Either precollege performance or SAT/ACT were reported as significant predictors in seven studies.
Gym grade . This variable was not assumed as a predictor of persistence in the 16 articles reviewed. Yet, based on Hirschi's ( 1969 ) theory of social bonding (i.e., attachment, commitment, involvement, and belief), the gym grade may correlate with persistence. According to the results of empirical studies ( Braddock, 1981 ; McNeal, 1995 ; Melnick, Sabo, & Vanfossen, 1992 ), participation in athletic activities reduced a student's likelihood of dropping out. Thus, we suggest the gym grade is a potential predictor of persistence in Taiwan.
| Figure 1 |
|---|
| The conceptual model of college student persistence on which this study is based. |
|
Major departments . Because each student has his educational goal and the department's commitment, the major department is assumed as a predictor of persistence. The major department is a significant predictor of persistence in four empirical studies.
Housing . Pascarella and Chapman ( 1983 ) studied college withdrawal and found living in a dormitory had a direct effect on persistence for four-year residential colleges. Because students who live on campus may have more opportunities to join in campus activities, corresponding to social bonding theory, they may decide not to leave college.
Occupational guidance program . Vocational education program (VEP) status was a significant predictor of persistence in Webb's ( 1988 ) study. This predictor is similar to the variable of vocational guidance program (VGP). Students in VGP may better understand what their future will be and what they should do; a higher persistence rate can be expected for those students enrolled in vocational guidance programs.
Academic remedial program . Academic integration or success was a significant predictor of persistence. If students enroll in the remedial program, they may foresee that they can get higher grade-point-average (GPAs) and then probably persist in college.
In summary, with variables specified in the former paragraphs, we propose Figure 1 as the conceptual model. In the model, persistence is the dependent variable. The independent variables that correlate with persistence are gender, parental education, entrance examination scores, academic GPA_1 (first semester), academic GPA_2 (second semester), social integration_1 (first semester), social integration_2 (second semester), major departments, academic remedial program, occupational guidance program, housing, gym grade_1 (first semester), and gym grade_2 (second semester). The methods to test the model conceptualized will be expressed in the next section.
Method
The participants were 1,243 anonymous vocational-technical college freshmen. Two college data files were the sources of data. One file was in the office of the registrar, and the other was in the office of student general affairs. We assigned freshman-year to sophomore-year persistence as the dependent variable. It was coded "1" for persistence (i.e., students enrolled at the same college for the next semester) and coded "0" for nonpersistence (i.e., students left school in the next semester).
Statistical Analysis
The analysis methods used in the 16 empirical studies cited were diverse. Except for the differences of variables and conceptual models, we found that the models were merged and modified, and the improvement of statistical methodology made a difference. Because the outcome is dichotomous and the purpose is to predict, logistic regression analysis can be used. Logistic regression does not adhere to assumptions about the normality of distribution nor the constant variance ( Tabachnick & Fidell, 1996 ; Tate, 1995 ). Other researchers (e.g., St. John & Starkey, 1996 ; Stage, 1988 , 1989 ) have also used logistic regression to develop models.
Procedures
The study was carried out in steps: to screen out outliers, to assess the model's goodness-of-fit and to build empirical models, to conduct the case analysis, and to predict probability of student persistence. We will focus on assessing and constructing the model and prediction.
Test of model-goodness-of fit . Logistic regression can be represented by the logit equation ( Equation 1 ) and the probability function ( Equation 2 ). In Equation 2, P is the probability of persistence. To test the null hypothesis, the chi-square statistic should compare to the critical value (Tate, 1995).
g = B 0 + B 1 X 1 + B 2 X 2 + … + B k X kEquation (1) exp(g) 1 P = ------------- or P = --------------- Equation (2) 1 + exp(g) 1 + exp(-g)Where exp( g ) represents the constant, e = 2.718, raised to the power g .
Model parameter estimation . To estimate a model parameter, the researcher needs to test the overall relationship of the outcome and predictors. The statistic -2 log Likelihood can be calculated by:
-2 LL = _ [ Y i ln( P i ) + (1 - Y i ) ln(1 - P i )], where Y i is the actual outcome (either equal to 1 or 0), and P i is predicted probability ( Tabachnick & Fidell, 1996 ).
Identification and prediction . With the empirical model constructed, the probability of persistence for a student is calculated by the combination of Equations 1 and 2, and the combined equation can be used to identify at-risk students who are in high probability of leaving college.
In summary, because persistence was the dichotomous dependent variable, logistic regression was used to analyze data, and models of persistence were constructed and presented in figures and equations. Data analysis produced the following results.
Results
Based upon the analysis of 1,243 freshmen records, the persistence rate was about 69%. We used the logistic regression methods of Enter and Fstep to analyze data. Because the Enter method was the best method that could classify nonpersistence (66.8%), we used the results to construct the primary persistence model ( Figure 2 and Equation 3 ). The regression coefficients are listed in Table 1 . Second, we used the Fstep method to identify significant predictors and used these significant variables to construct the secondary persistence model ( Figure 3 and Equation 4 ). The regression coefficients are listed in Table 2 .
Primary Persistence Model
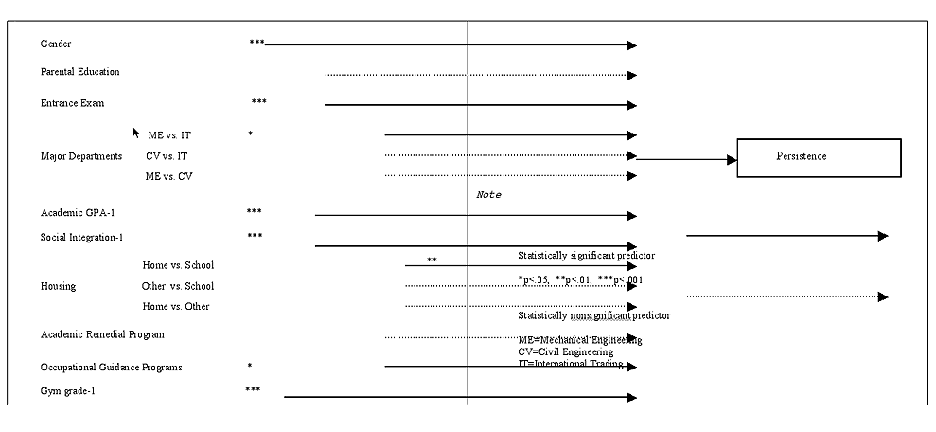
This model includes 14 independent variables. However, it should be noted that Major Departments and Housing are made up of 3 variables each. These two sets of variables are dummy variables and thus reduce the number of variables in the equation to 12. The cut value (i.e., the value to classify an individual into the persistence or the nonpersistence group) was set at 0.61 in order to obtain the maximum overall classification rate. The cut value of .61 was identified to maximize the number of correct classifications of presisters and non-persistors. After the analysis processes of test of model-goodness-of fit, model parameter estimation, classification of individuals, and case analysis, a primary
Table 1 Regression Coefficients and Effects in Standardized Score for the Primary Model
Variable B S.E. Sig R Effect
Academic Remedial .039 .157 .806 .000 1.039 Academic GPA1 .562 .089 .000 .158 1.754 Dept. Civil Eng. -.453 .260 .081 -.026 .636 Dept. Mech. Eng. -.635 .257 .014 -.052 .530 Entrance Exam .618 .079 .000 .196 1.855 Parent Educ. .072 .074 .329 .000 1.075 Gender -1.003 .178 .000 -.139 .367 Gym Grade .260 .074 .001 .082 1.297 Housing - Home .574 .376 .128 .015 1.775 Housing - School -.285 .277 .303 .000 .752 Occupational Guid. .332 .156 .033 .041 1.394 Social Integ. 1 .339 .074 .000 .111 1.403
persistence model was constructed and presented in Figure 2 . The logit function for future prediction or classification is the following (Equation 3):
g = -14.5118 - 1.0031 (gender; M=1, F=0) + 0.3321 (occupational guidance; Y=1, N=0) + 0.0386 (academic remedial; Y=1, N=0) + 0.5737 (living at home; Y=1, otherwise=0) - 0.2849 (living at school; Y =1, otherwise=0) - 0.6345 (mechanical engineering major; Y=1, otherwise=0) - 0.4528 (civil engineering major; Y=1, otherwise=0) + 0.0721 (first semester academic GPA) + 0.0411 (first semester social integration) + 0.0395 (first semester gym grade) + 0.0139 (years of parental education) + 0.0121 (entrance examination score). Equation (3)
Table 2
Regression Coefficients and Effects in Standardized Score for the Secondary Model
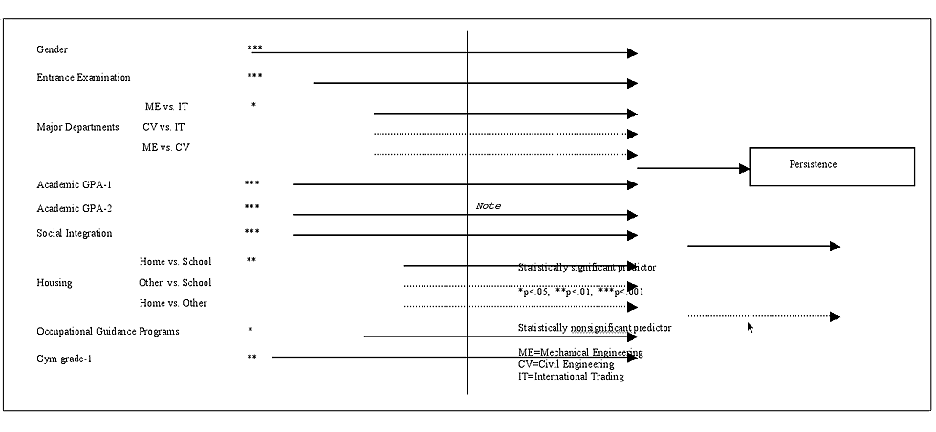
Variable B S.E. Sig R Effect Academic GPA1 .447 .093 .000 .117 1.563 Dept. Civil Eng. -.384 .263 .144 -.010 .681 Dept. Mech. Eng. -.569 .260 .029 -.043 .566 Entrance Exam .620 .080 .000 .195 1.859 Gender -.960 .180 .000 -.132 .383 Gym Grade1 .205 .076 .007 .059 1.228 Housing - Home .795 .285 .005 .062 2.215 Occupational Guid. .304 .152 .046 .036 1.355 Social Integ. 1 .299 .075 .000 .095 1.348 Housing - Other .261 .275 .342 .000 1.299 Academic GPA2 .323 .088 .000 .087 1.381
Secondary Persistence Model
First, we used the Fstep method to test the statistical significant of 13 predictors six of which were dummy variables (see Figure 1 ). Then, through the processes of Enter method analysis, a secondary model with 11 predictors, which also included the two sets of dummy variables, was constructed in Figure 3 . Taking regression coefficients to construct a function for future prediction is (Equation 4):
g = -14.6205 - 0.9603 (gender; M=1, F=0) + 0.3038 (occupational guidance; Y=1, N=0) + 0.7952 (living at home; Y=1, otherwise=0) - 0.2612 (living at neither home nor school; Y=1) - 0.5694 (mechanical engineering major; Y=1) - 0.3844 (civil engineering major; Y=1) + 0.0574 (first semester academic GPA) + 0.0363 (first semester social integration) + 0.0312 (first semester gym grade) + 0.0297 (second semester academic GPA) + 0.0122 (entrance examination score). Equation (4)
| Figure 2 |
|---|
| Primary college student persistence model. |
|
Summary of Models
The primary model supports the conceptual model (see Figure 1 ) with eight significant predictors. A combination of Equations 2 and 3 can be used to predict the student probability of persistence at the end of first semester. The first semester model correctly classified 66.84% nonpersistors, 81.58% persistors, and 77.07% overall correct classification (see Table 3 ). The secondary model also supports the conceptual model with nine significant predictors. The combination of Equations 2 and 4 can be used to predict the student probability of persistence at the end of the second semester. The secondary model was able to classify correctly 69.21% nonpersistors, 82.04% persistors, and 78.12% overall correct classification (see Table 4 ). All three (persistence, nonpersistence, and overall) classification rates of the secondary model are greater than that of the primary model. Yet, the primary model can be used to classify early most students who are prone not to persist at an early point in their education. The implications and applications about models and equations are discussed in the next section.
Discussion
We used the example cases to illustrate how to use the models in equation form. The implication and application of the primary and secondary persistence models are also addressed in this section.
Table 3 The Primary Model Classification Table
Predicted outcome Correctly classafied 0 1
Observed
outcome0 254
(66.84%)126
(33.16%)66.84% Nonpersist 1 159
(18.42%)704
(81.58%)81.58% Persist
Overall correctly classified 77.07%
| Figure 3 |
|---|
| Secondary college student persistence model. |
|
Table 4 The Secondary Model Classification Table
Predicted outcome Correctly classafied 0 1
Observed
outcome0 263
(69.21%)117
(30.79%)69.21% Nonpersist 1 155
(17.96%)708
(82.04%)82.04% Persist
Overall correctly classified 78.12%
First-Semester Persistence Model
The combination of Equations 2 and 3 can be used to estimate the probability of first-semester persistence, e.g., cases A and B. For student-A, the logit and the probability of persistence are calculated as (Equations 5 and 6):
g = -14.5118 - 1.0031 (1) + 0.3321 (0) + 0.0386 (0) + 0.5737 (0) - 0.2849 (1) - 0.6345 (1) - 0.4528 (0) + 0.0721 (79) + 0.0411 (90) + 0.0395 (77) + 0.0139 (18) + 0.0121 (336) = 0.3179.Equation (5)
1 1 P = --------------- = --------------------- = 0.5788 Equation (6) 1 + exp(-g) 1 + exp(-0.3179)The resulting probability of persistence for student-A is 0.5788. When the cut point probability was set at 0.61, student-A was incorrectly classified, because the persistence variable of student-A is 1, but he or she is assigned to the nonpersistence group. Similarly, to calculate the probability of persistence for student-B, the result is P = 0.5009; student-B is correctly classified as a nonpersistor. When using Equation 2 and 3, the probability of persistence for each student can be calculated at the end of the first semester by using Equations 5 and 6.
Second-Semester Persistence Model
The combination of Equations 2 and 4 can be used to calculate the probability of persistence at the end of the second semester. For student-A, the probability of persistence is equal to 0.631. With the cut point probability set at 0.62, the probability that maximized the number of correct classifications, student-A is correctly classified (notice that student-A was mis-classified at the end of first semester). For student-B, the calculation is the following (Equations 7 and 8):
g = -14.6205 - 0.9603 (1) + 0.3038 (0) + 0.7952 (0) - 0.2612 (0) - 0.5944 (0)- 0.3844 (1) + 0.0574 (61) + 0.0363 (93) + 0.0312 (67) + 0.0297 (62) + 0.0122 (412) = -0.1279Equation (7)
1 1 P = --------------- = -------------------- = 0.4676 Equation (8) 1 + exp(-g) 1 + exp(0.1279)The probability of persistence for student-B is equal to 0.4676. Student-B is also correctly classified as nonpersistor at the end of the second semester. In the future, by using the first-year student's data and Equations 2 and 4, the freshman probability of persistence can be calculated at the end of the second semester by using Equations 7 and 8.
Conclusions
This section presents the influences of predictors on persistence, the reasons that some predictors are significant yet some are not, and the implications of primary and secondary persistence models. Finally, we state practical recommendations for the college to improve schooling and recommendations for future research.
Primary Persistence Model
We will discuss each predictor in Figure 2 or Equation 3 . The results of the primary regression supported eight assumed predictors but did not support two assumed predictors. The implications and rationale of predictors follow.
First semester academic GPA . The student with a high GPA has a higher probability of persistence, provided that other predictors are controlled. Controlling for other predictors is also applied to later comparisons about probability of persistence. This result is consistent with suicide and turnover theories and results of past empirical studies (e.g., Bean, 1980 ; Chen, 1988 ; Chen & Chen 1988 ; Hwang, 1994 ; Kao, 1996 ; Lin, 1975 ; Liu, 1994 , 1995 ; St. John & Starkey, 1996 ; Xie, Shu, & Guo, 1983 ).
Gender . The female student has a higher probability of persistence than does the male student. The relationship between gender and persistence has been found in many studies presented in the literature review. For this sample, the gender difference is consistent with previous findings (e.g., Chen, 1988 ; Liu, 1994 ; Metzner, 1989 ; Spady, 1971 ).
Entrance examination . The student with high entrance examination scores has a higher probability of persistence. This result is consistent with the theory that prior knowledge may facilitate later learning ( Anderson, 1985 ) and with empirical findings in the literature (e.g., Spady, 1971 ; Webb, 1983 ) that precollege performance is a significant predictor of persistence.
Major departments . The choice of department reflects the student's educational goal and the student's commitment to the department. Thus, a student with a high degree of commitment to a department has high inclinations toward persistence. This result is consistent with previous findings ( Kao, 1996 ; Lo & Lee, 1982 ; Stage & Rushin, 1993 ).
First-semester social integration . The student with a high social integration has a higher probability of persistence. This result is consistent with suicide and turnover theories and former empirical studies (e.g., Liu, 1995 ; Stage & Rushin, 1993 ; Young, 1982 ).
Housing . Social bond theory (i.e., attachment to others and involvement in activities decrease isolation) and Pascarella and Chapman's ( 1983 ) findings would lead us to conclude that living on campus and away from home would result in higher persistence rates. Yet, our finding that location of residence did not increase our probability of predicting persistence. The finding that location of housing did not contribute to persistence may be contrary to the findings in the United States for a number of reasons including negative dormitory situations (e.g., too many students living in a small room, bad food, and lack of good administration of the dormitory) or the avoidance of homesickness or both.
First-semester gym grade . The student with a high gym grade has a higher probability of persistence. This result is consistent with the social bond theory (i.e., commitment to conformity and involvement in activities increase human relationships) and empirical studies ( Braddock, 1981 ; McNeal, 1995 ; Melnick, et al., 1992 ) that participation in athletic activities increases the student's likelihood of persistence.
Occupational guidance programs . Students enrolled in occupational guidance programs have a higher probability of persistence than those who not so enrolled. Because a future occupation may motivate students to persist in the college ( McKinney, Lorion, & Max, 1976 ), students in the programs know what their futures may be and what they will do. The similar result was found in Webb's ( 1988 ) study that vocational education program status was a significant predictor of freshman-year persistence.
Parental education . Presented in human capital theory ( Becker, 1964 ), parental education is one of the indices of SES. Students' parents in high level SES are able to pay tuition and expenses. Studies (e.g., Lin, 1975 ; Eaton & Bean, 1995 ; Stage, 1989 ) showed that high SES correlated with persistence. However, if the tuition and expenses are not very high as after in Taiwan after 1990 or generally low-interest student loans which have a simple application process are readily available, this family SES predictor may be nonsignificant ( Becker, 1964 ). The nonsignificant result was also found in other studies (e.g., Cabrera, et al., 1993 ; Xie, et al., 1983 ).
Academic remedial program . The absence of a significant relationship between this predictor and persistence may mean that students who enrolled in the program did not benefit academically ( Kulik, Kulik, & Shwalb, 1983 ), or that students with low entrance examination scores evaded enrolling in the program (e.g., Eaton & Bean, 1995 ).
Secondary Persistence Model
Eleven predictors were used by the Enter method to construct the secondary persistence model ( Figure 3 ). We will identify predictors that were and were not specified in the primary persistence model.
Significant predictors . The results of the secondary regression supported nine assumed predictors. Of the nine predictors, eight of them have been discussed. The ninth significant predictor is the second-semester academic GPA. Students with a high second-semester academic GPA have a higher probability of persistence, when other predictors are controlled. Because high academic GPA students may be satisfied and confident, they decide to persist. This result is consistent with suicide and turnover theories and past empirical evidence.
Nonsignificant predictors . Second-semester social integration and second-semester gym grades are variables that were not supported by the results of the analysis. Based upon social bond theory, since the social bonds are saturated in the first semester (e.g., during the first semester, students adjust to the college circumstances and build up human relationships) ( Bruno, 1977 ; Calhoun & Acocella, 1978 ), in the second semester, the social bond does not increase. Thus, the second-semester bonding score adds very little to predicting persistence. It is recommended that the primary model be used at the end of the first semester and the secondary model at the end of the second semester to predict college freshman persistence probability. More recommendations follow.
Practical Recommendations
The results indicate that several practices may be considered to identify dropping out and to increase persistence.
- The application of the persistence models developed in the United States were found to be useful in Taiwan to build models that be of assistance to vocational educators in identify students who have a high likelihood of dropping out of technical schools. The set of variables, though not exactly mirroring those from studies in the U.S., adhere very closely to the identified models. It is recommended that the models developed be employed to identify students who have a high likelihood of dropping out so that these students can be provided assistance to resolve identified problems.
- The first and second semester GPAs significantly influence persistence, but participation in an academic remedial program does not. The college administrator should make changes designed to improve teaching and learning in regular class to assist students in earning higher GPAs, thus increasing student persistence.
- The administration should investigate to determine effectiveness of the remedial program to see if the identified objectives are being met and, if so, to identify the lack of relationship of the remedial program with persistence.
- Faculty and student affairs staff should be advised that the male and female students leave college for different reasons (e.g., housing and major departments). Any program or policy designed to increase student persistence should take gender difference into account.
- The college advisors should strive to attract students with low entrance examination scores and a low first-semester academic GPA into vocational guidance programs. These programs foster an increase in the students' knowledge of occupational goals and enhance interactions with faculty and peers, thus probably increasing persistence.
- Because the gym grade is a significant predictor, the gym instructors and the class advisors should notice those students who do not like to join athletics or extracurricular activities. Instructors and advisors may work together encouraging and assisting students to build up their participation in exercise customs and to join campus activities. It should be noted that the gym grade in Taiwan is similar to a social integration score in the U.S.
The Research Recommendations
This study can be useful in introducing further persistence research that constructs freshman-year models at the end of the first and second semesters. Several recommendations for future study are as follows.
- Logistic regression analysis is an appropriate and practical statistical exploratory analysis to classify significant predictors and to construct the persistence model. We recommend using logistic regression analysis in future exploratory research concerning persistence.
- Pascarella and Chapman ( 1983 ) reported a pooled classification rate that was 70% ( p. 94 ). In this study, the overall classification rate for the primary model is 77% and for the secondary model the rate is 78%. In future research, for comparison, reporting predicted outcomes in classification tables as presented in Tables 3 and 4 is recommended.
- The causal models built in this study may not be suitable for other colleges to predict their student persistence, because the model may be quite different at low- and high-prestige colleges, large and small schools, and two-year, four-year, and five-year institutions. Yet, the variables of gender, academic GPA, precollege experience, ethnicity (in the U.S.), housing, major departments, social integration, and gym grade should be taken into consideration.
- To improve classification rates, researchers may include constructs such as "value" ( Ethington, 1990 ), "occupational predisposition," and other psychological variables (e.g., approach or avoidance attitude, Bean & Eaton, 1995 ; personality, Johnson & Buck, 1995 ) in conducting research on persistence.
- The college researcher may be well advised to construct or revise the models every one or two years to better identify students at-risk of dropping out. This recommendation is based on the fact that the data are easy to access from permanent records and that interventions may change the weights of variables being used.
References
Anderson , J. R. (1985). Cognitive psychology . New York: W. H. Freeman and Company.
Bean , J. P. (1980). Dropouts and turnover: The synthesis and test of a causal model of student attrition. Research in Higher Education , 12 (2), 155-187.
Bean , J. P. (1986). Assessing and reducing attrition. Managing College Enrollments , 14 (1), 47-61.
Bean , J. P., & Metzner, B. S. (1985). A conceptual model of nontraditional undergraduate student attrition. Review of Educational Research , 55, 485-540.
Becker , G. S. (1964). Human capital: A theoretical and empirical analysis with special reference to education . New York: National Bureau of Economic Research, Columbia University Press.
Braddock , J. H., II (1981). Race, athletics, and educational attainment. Youth and Society , 12, 335-350.
Cabrera , F. C., Nora, A., & Castaneda, M. B. (1993). Structural equations modeling test of an integrated model of student retention. Journal of Higher Education , 64, 123-139.
Cabrera , A. F., Stampen, J. O., & Hansen, W. L. (1990). Exploring the effects of ability to pay on persistence in college. The Review of Higher Education , 13, 303-336.
Chen , C., & Chen, Z. (1988). Investigating causes of dropping out in Open University (Research Report No. 3). Taiwan, ROC: Open University.
Chen, T. (1988). The factors of dropping out for supplement college adult students . Unpublished master's thesis, National Taiwan Normal University, Taipei, ROC.
Chiu , W. (1994). Models of dropouts and strategies for guidance. Journal of Bimonthly Educational Research , 36, 32-41.
Cohen , J. (1977). Statistical power analysis for the behavioral sciences . New York: Academic Press.
Cronbach , L. J. (1970). Essentials of psychological testing . New York: Harper & Row, Publishers.
Durkheim , E. (1951). Suicide . (J. A. Spaulding & G. Simpson, Trans.). Glencoe, IL: The Free Press.
Eaton , S. B., & Bean, J. P. (1995). An approach / avoidance behavioral model of college student attrition. Research in Higher Education , 36, 617-645.
Ethington , C. A. (1990). A psychological model of student persistence. Research in Higher Education , 31, 279-293.
Halpin , R. L. (1990). An application of the Tinto's model to the analysis of freshman persistence in a community college. Community College Review , 17 (4), 22-32.
Hirschi , T. (1969). Causes of delinquency . Los Angeles: University of California Press.
Hwang , F. (1994). The adult dropouts and handling strategy. Journal of Bimonthly Educational Research , 36, 20-26.
Kao , C. (1996). A study on dropout tendency of students in vocational supplementary school. Journal of National Taiwan Normal University Social Education , 25, 233-251.
Kulik , C. C., & Kulik, J. A. (1991). Effectiveness of computer-based instruction: An updated analysis. Computers in Human Behavior , 7 (1-2), 75-79.
Kulik , C. C., Kulik, J. A., & Shwalb, B. J. (1983). College programs for higher-risk and disadvantaged students: A meta-analysis of findings. Review of Educational Research , 53, 397-414.
Lin , M. (1975). Chinese and American college student attrition . Taiwan, ROC: National Chan-Chi University Guidance Center.
Liu , S. (1994). Analyzing open university and college dropouts. Bimonthly Educational Research , 36, 13-19.
Liu , S. (1994). Constructing measurement equations for Commercial Open College students. Journal of Elementary Education , 3, 265-314.
Lo , Z., & Lee, T. (1982). The problems of transferring schools and changing majors at Kao-Shong high and vocational high schools. National Kao-Shong Teacher College Educational Editions , 11, 152-162.
McKinney , F., Lorion, P.R., & Max, M. (1976). Effective behavior and human development . New York: Macmillan Publishing Co., Inc.
McNeal , , R. B., Jr. (1995). Extracurricular activities and high school dropouts. Sociology of Education , 68, 62-81.
Melnick , M. J., Sabo, D. F., & Vanfossen, B. (1992). Educational effects of interscholastic athletic participation on African-American and Hispanic youth. Adolescence , 27, 106, 295-308.
Metzner , B. S. (1989). Perceived quality of academic advising the effect on freshman attrition. American Educational Research Journal , 26, 422-442.
Nora , A., Attinasi, L. C., Jr., & Matonak, A. (1990). Testing qualitative indicators of precollege factors in Tinto's attrition model: A community college student population. The Review of Higher Education , 13, 337-356.
Nora , A., & Cabrera, A. F. (1996). The role of perceptions of prejudice and discrimination on the adjustment of minority students to college. Journal of Higher Education , 67 (2), 119-148.
Norusis , M. (1997). SPSS professional statistics 7.5 . Chicago: SPSS Inc.
Norusis , M. J. (1994). SPSS advanced statistics 6.1 . Chicago, IL: SPSS Inc.
Pascarella , E. T. (1980). Student-faculty informal contact and college outcomes. Review of Educational Research , 50, 545-595.
Pascarella , E. T., & Chapman, D. W. (1983). A multi-institutional, path analytic validation of Tinto's model of college withdrawal. American Educational Research Journal , 20 (1), 87-102.
Pascarella , E. T., & Terenzini, P. T. (1979a). Interaction effects in Spady's and Tinto's conceptual models of a college dropout. Sociology of Education , 52, 197-210.
Pascarella, E. T., & Terenzini, P. T. (1979b). Student-faculty informal contact and college persistence: A further investigation. Journal of Educational Research , 72, 214-218.
Pascarella, E. T., & Terenzini, P. T. (1983). Predicting voluntary freshman year persistence/withdrawal behavior in a residential university: A path analytic validation of Tinto's model. Journal of Educational Psychology , 75, 215-226.
Price , J. L. (1977). The study of turnover . Ames: Iowa State University Press.
Spady , W. G. (1970). Dropouts from higher education: An interdisciplinary review and synthesis. Interchange , 19 (1), 109-121.
Spady , W. G. (1971). Dropouts from higher education: Toward an empirical model. Interchange , 2 (3), 38-62.
Stage , F. K. (1988). University attrition: LISREL with logistic regression for the persistence criterion. Research in Higher Education , 29, 343-357.
Stage , F. K. (1989). Motivation, academic and social integration, and the early dropout. American Educational Research Journal , 26, 385-402.
Stage , F. K., & Rushin, P. W. (1993). A combined model of student predisposition to college and persistence in college. Journal of College Student Development , 34, 276-282.
St. John , E. P., & Starkey, J. B. (1996). An alternative to net price: Assessing the influence of prices and subsidies on within-year persistence. Journal of Higher Education , 66, 156-186.
Tabachnick , B. G., & Fidell, L. S. (1996). Using multivariate statistics . New York: Harper Collins.
Tate , R. (1995). Modeling outcomes in the behavioral and social science . Tallahassee, FL: Target Copy.
Terenzini , P. T., & Pascarella, E. T. (1980). Toward the validation of Tinto's model of college student attrition: A review of recent studies. Research in Higher Education , 12, 271-282.
Tinto , V. (1975). Dropout from higher education: A theoretical synthesis of recent research. Review of Educational Research , 45 (1), 89-123.
Tinto , V. (1982). Limits of theory and practice in student attrition. Journal of Higher Education , 53, 687-700.
Tinto , V. (1993). Leaving college . Chicago: University of Chicago Press.
Tinto , V., Russo, P., & Kadel, S. (1994). Constructing educational communities. Community College Journal , 64 (4), 26-29.
Tinto , V., & Wallace, D. L. (1986). Retention: An admission concern. College and University , 61, 290-293.
Webb , M. W. (1988). Freshman year retention at three campuses of a large urban community college district: 1983-1986. Community/Junior College Quarterly , 12, 213-242.
Webb , M. W. (1989). A theoretical model of community college student degree persistence. Community College Review , 16 (4), 42-49.
Xie , C., Shu, G, & Guo, Y. (1983). Investigating and analyzing Kaushong high school dropouts . Taiwan, ROC: Kaushong Chenchang High School.
Xu , G. (1993). Longitudinal comparison of the academic performance of Asian-American and white medical students. Academic Medicine , 68 (1), 82-86.
Zuckerman , M. B. (Ed.). (1996). America's best college [Special issue]. US News & World Report.
Authors
SEA-SHON CHEN is associate professor at the Dahan Institute of Technology, Taiwan, Korea, P.O.Box 9-26, Hualien, Taiwan, R.O.C. [E-mail: seachen@ms8.tisnet.net.tw ; seashon.chen@msa.hinet.net ]. His research interest is educational leadership in vocational education.
HOLLIE THOMAS is professor at the Florida State University, 113 Stone Building, Department of Educational Leadership, Florida State University, Tallahassee, Florida 32306 [E-mail: hthomas@garnet.acns.fsu.edu ]. His research interest are career development and leadership in vocational education.