JVER v26n3 - A Question of Balance: CTE, Academic Courses, High School Persistence, and Student Achievement
A Question of Balance: CTE, Academic Courses, High School Persistence, and Student Achievement
Stephen B. Plank
Johns Hopkins UniversityAbstract
Educators, researchers, and policymakers are currently examining the ways that career and technical education (CTE) is-and could be-coupled with core academic education in U.S. high schools. This study discusses how CTE and academic curricula can, or should, co-exist. The study examines the relationship between (a) the balance struck between CTE and academic course-taking during the high school years, and (b) academic achievement and persistence in high school. Data come from the National Education Longitudinal Study of 1988. The balance between CTE and academic course-taking is shown to have some influence on both test scores and the likelihood of dropping out, with effects being most dramatic and noteworthy for likelihood of dropping out. Specifically, the analyses suggest that a ratio of approximately three CTE credits to every four academic credits was associated with the lowest likelihood of dropping out for this sample. Implications for policy, practice, and future research are discussed.
As a society, we ask a lot of our high schools. We ask them to promote students' proficiency in multiple core academic areas. We ask them to prepare individuals for postsecondary endeavors, whether participation in the labor force, continuing education, or both. We ask high schools to develop or encourage certain socially desired behaviors, attitudes, and capacities in students, while discouraging or sanctioning other traits and behaviors. And-as we ask schools to pursue these varied and sometimes competing goals-we hope they will make the experience engaging and rewarding enough to convince students to remain within the formal educational system at least until high school graduation; we hope students will persist to graduation rather than dropping out of school.
Not only does society present high schools with a diverse set of goals; our demographic and social make-up also presents high schools with a diverse set of students to be guided and educated. Individuals enter high schools with different levels of academic preparation, a variety of home and neighborhood backgrounds, varying degrees of commitment to formal educational endeavors, and a wide range of desires and expectations for the years after high school.
Not surprisingly, in the face of multiple societal mandates and diverse student populations, high schools in the United States have come to offer multiple and varying curricular paths for students to follow (Hallinan, 1994 ; Oakes, 1994 ; Oakes, Gamoran, & Page, 1992 ; Powell, Farrar, & Cohen, 1985 ). Which path a student will follow-what balance of specializations and subject areas he or she will be exposed to-is partly a matter of individual choice and partly a matter of being guided or placed by the adults and sorting mechanisms of schools as organizations (Garet & DeLany, 1988 ).
Career and technical education-or vocational coursework-is a notable part of the mix. For many decades, high schools seemed to focus on preparing students for either entry-level jobs or postsecondary education. Students who were being guided toward labor force entry immediately after secondary school often completed many of their high school credits in areas such as trade, industry, business, agriculture, marketing, and distribution. Students who were being prepared for postsecondary education generally took fewer of these vocational courses and instead completed more credits in mathematics, science, English, social studies, and foreign language.
These two distinct trajectories of vocational concentration and college preparation (and others that completed the menu of available paths) have not ceased to exist. However, a couple of trends have altered the landscape of the U.S. high school. First, during the 1980s and into the 1990s, the amount of high school vocational course-taking declined while academic course-taking increased (Hoachlander, Kaufman, Levesque, & Houser, 1992 ; Levesque et al., 1995 ; Levesque, Lauen, Teitelbaum, Alt, & Librera, 2000 ). The reasons for this shifting balance are surely complex, but contributing factors include changes in high school graduation requirements and changes in the skill sets and training levels demanded by the labor market (National Center for Education Statistics, 2000 ).
Second, explicit attempts to combine vocational education with a solid academic grounding have become increasingly common. One central goal of such integrated programs is to keep individuals' options open until after high school. If high-quality preparation in core academic subjects can be coupled with a strong foundation in work skills and applications, it is hoped that upon high school graduation individuals will have attractive options available in multiple arenas: in two- or four-year colleges, within the paid labor force, or in pursuing postsecondary education and paid employment simultaneously.
Advocates of combining vocational concentration with college preparation also suggest motivational benefits. In light of increasingly stringent high school graduation requirements in most states, we can assume that almost all high school students will be exposed to more core academic subjects (in particular, English, mathematics, science, and social studies) than would have been typical 10 or 20 years ago. Given this fact, are there reasons to expect that students will perceive greater relevance in academic subjects, apply greater effort to their academic courses, or develop firmer commitment to school, generally, if academic studies are coupled with career and technical education (CTE)? Many argue that indeed there are reasons to expect these motivational benefits.
Positing such potential benefits, Crain et al. ( 1998 ) studied students' experiences in career-focused magnet high schools. In describing an ideal in career magnet design and implementation, Crain and his colleagues seem to hypothesize the greatest potential benefits for students exhibiting average or somewhat-below-average achievement levels upon entering high school. Their comments about potential benefits of career magnet programs can logically be extended to efforts to combine CTE and academic course-taking more broadly. They wrote the following:
Abstract academic education not connected to a specific career can be satisfying only to those students who are certain they will get a four-year college degree that will meet their career-preparation needs. Contrasted with the traditional high school, career magnets can command the loyalty of their students and offer them an opening to a future career that does not require them to be part of the academic elite (Crain et al., 1998 , p. 4).
Extending the ideas of Crain and his colleagues to more general efforts to combine CTE and academic courses simply requires the following perspective: For students who do not see a four-year college degree as a definite desire or a certainly attainable goal, academic courses isolated from CTE exposure would be likely to seem irrelevant or frustrating. A student who did not feel sure that he or she would be able to enter a four-year college, or that he or she would want to enter a four-year college, would be likely to find limited meaning and excitement in studying solely core academic subjects. On the other hand, if academics were properly integrated with career-focused courses, such a student might see practical applications of the mathematics, science, reading, writing, and cultural studies contained within academic courses. Such a student with dual CTE and academic concentrations might apply greater effort to his or her academic studies than would a student encountering only academic courses.
According to this perspective, a student's cognitive growth in the core academic subjects could be expected to be augmented when CTE and academic course-taking were featured jointly, as compared to when an academic concentration was featured alone. This might be especially the case for low-achieving students. Further, a student's general enthusiasm and attachment to high school could be expected to increase-and, thus, his or her risk of dropping out to decrease-when CTE and academic course-taking were coupled. These, of course, are hypotheses. They are hypotheses that have been investigated in some previous research (Boesel & McFarland, 1994 ; Boesel, Hudson, Deich, & Masten, 1994 ; Crain et al., 1999 ; Delci & Stern, 1999 ; Levesque et al., 2000 ; National Center for Education Statistics, 1999a ; Rasinski & Pedlow, 1998 ), and they will be explored further in this article.
There are reasons to temper these hypotheses. Specifically, regarding effects on cognitive growth in academic subjects, some educators worry that combining CTE with an academic course load dilutes the quality and quantity of academic coverage. Indeed, there are limits to the total number of courses students can take during their high school careers. If CTE occupies a significant portion of a student's schedule, this limits the hours remaining available for core academic subjects. Thus, even if a dual CTE/academic concentration has motivational benefits that lead students to apply greater effort to academic courses, the limits that the dual concentration places on overall exposure to academic topics might have countervailing effects on achievement growth. Within this article, attention will be paid to these issues.
Another caveat that should be attached to the hypothesized benefits of a dual CTE/academic concentration involves the precise nature or character of an integrated curriculum. For any possible benefits to accrue, do the teachers of CTE and academic courses in an integrated program need to prepare lessons and teach in close collaboration with one another? Must mathematics and science teachers make explicit efforts to illustrate linkages between their subjects and career applications in order for potential motivational and achievement benefits to accrue? Must CTE teachers forge explicit connections to the academic subjects in their instruction for benefits to be realized? Or, will benefits be realized simply by exposing students to both types of course-taking, without radical changes in classroom practices or fundamental efforts at integrated planning and instruction? The questions posed in this paragraph are beyond the capacity of this study's data set. Crain and his colleagues ( 1998 , 1999 ) have offered some evidence suggesting that some benefits can be realized even without radical changes to classroom and school organization, and without much joint planning and integrated instruction. This initial evidence is important, and as future research is conducted on dual CTE/academic concentrations, more attention should be paid to these matters. Within the present study, however, there is much to analyze and summarize without even broaching these nuances.
Research Questions
Within the context of the multiple missions of high schools, diverse student populations, and evolving curricular organization, this study aims to increase our understanding of the relationship between (a) the balance struck between career and technical course-taking and academic course-taking during the high school years, and (b) academic achievement and persistence in high school.
More specifically, this study addresses a series of interrelated questions for a nationally representative sample of public high school attendees who had been eighth graders in 1988. The study asks the following:
- For this sample, what balance was struck between CTE and academic course-taking?
- Can we detect effects of the balance between CTE and academic course-taking on achievement growth, as measured by standardized tests in the areas of mathematics, science, reading, and history?
- Can we detect effects of the balance between CTE and academic course-taking on the likelihood of dropping out of high school (or, conversely, persisting in high school)?
Data and Methods
The data for this study come from the National Education Longitudinal Study of 1988 (NELS:88), supported by the National Center for Education Statistics of the U.S. Department of Education. NELS:88 provides a rich source of information on adolescents and young adults as they progress through high school and into postsecondary education and the labor force. The NELS:88 base-year design employed a two-stage stratified random sample of approximately 25,000 eighth graders in more than 1,000 schools in 1988, who were then re-surveyed at two-year intervals through 1994 (Ingels, Abraham, Spencer, & Frankel, 1989 ; National Center for Education Statistics, 1996 ). In addition to student surveys and cognitive tests, the database includes survey responses from parents, teachers, and school administrators. Also, of central importance to the present study, NELS:88 includes transcript data, collected after the 1991-92 school year and covering all of a student's high school years.
In order to understand what the NELS:88 (hereafter identified simply as NELS) data can tell us about the effects of CTE and academic course-taking on high school persistence and academic achievement, it is important to note that most of the sample members graduated from high school in 1992. As such, their secondary school careers took place while the nature and quantity of vocational and college preparatory course-taking were still very much in transition in the United States. The 1990 Perkins Act, which encouraged a more integrated approach to CTE and college preparatory education, was probably just beginning to affect curricular organization. Legislation of the 1998 Perkins Act-which further encouraged the integrative approach-was still several years away. Thus, we should think of this longitudinal data set as one that can give us insights into trends and relationships as they existed in the earliest stages of the current wave of CTE reforms. Analyses of more recent data sets will be important as complements to studies such as the present one. The National Longitudinal Study of Youth 1997 promises to be one valuable source of comparisons, and analyses of vocational programs using that data set have begun (e.g., Delci & Stern, 1999 ). Other studies of these data are part of the current work of the National Research Center for Career and Technical Education.
In the present study, all analyses are limited to students who attended public high schools, because very little CTE course-taking was reported within the private high schools of the NELS sample. This data trend and sample selection decision are consistent with other recent studies of CTE experiences in U.S. high schools using nationally representative data. Analyses of twelfth-grade academic achievement are further limited to students who remained in school for four years of high school (and, correspondingly, had four years of transcript data available). This screening decision was made due to the requirements of the variables used to indicate course-taking patterns, as will be described later in this article.
All analyses are weighted by the NCES-provided longitudinal panel weights for students participating in the transcript component of NELS. The use of these weights allows for projections to the population of American youth who were in the eighth grade in spring of 1988, subject to the caveats on sample screening provided in the preceding paragraph.
Models of 1992 cognitive achievement are presented for the following subject areas: reading comprehension, mathematics, science, and history/citizenship/geography. The test battery was developed by the Educational Testing Service. For the 1992 data collection (the NELS second follow-up), multiple forms of the cognitive test battery were produced, each comprising a different combination of mathematics and reading difficulty levels. Each sample member's test form was determined by his or her scores on the base-year and/or first follow-up mathematics and reading tests. The analyzed scores are based on Item Response Theory. Additional details on the NELS cognitive tests, including the strategies employed to minimize ceiling and floor effects, are provided in Ingels et al. ( 1994 ) and Rock and Pollack ( 1995 ).
The models of cognitive achievement in each of the four subject areas utilize multiple ordinary least squares regression, which is appropriate given the continuous dependent variable and the fact that we must include numerous contextual variables as regressors in order to control for potentially confounding factors as we focus on the effects of CTE and academic course-taking. In the tables that summarize the results of these models, unstandardized regression coefficients will be presented. These unstandardized coefficients reflect the number of test score points (or the portion of a test score point) that is added to, or subtracted from, an individual's predicted achievement level if a given independent variable increases by one unit, holding constant all other independent variables in the model.
The models of dropping out-which involve a nominal, dichotomous dependent variable and multiple independent variables-utilize logistic regression. In the table that summarizes the results of these models, the estimated coefficients will reflect the additive effect of the independent variables on the log-odds [ln(p/1-p)] of an individual dropping out of high school. While this log-odds metric is necessary for the estimation of the models, it is admittedly a somewhat difficult metric to interpret. Therefore, the estimated parameters in the log-odds metric will be used primarily to identify which independent variables have statistically significant associations with the likelihood of dropping out. More precise quantification and interpretation will be accomplished with reference to predicted probabilities, not predicted log-odds.
That is, the results in the log-odds metric will be used to highlight substantively important relationships. When we want to quantify and discuss the magnitude of these relationships more precisely, the appropriate mathematical transformations will be completed in order to translate predicted log-odds into predicted probabilities (p). A graph will be utilized to display the predicted probability of a hypothetical individual (e.g., a white male, who matches the sample means for eighth-grade test scores, grade point average, and SES, and who had a particular mix of CTE and academic course-taking during high school) dropping out of high school. To understand the origins of that graph, the reader should keep in mind that the predicted probabilities will be based upon the estimated logistic regression models.
Results
Distribution of Course-Taking
Before considering multivariate models of the two main outcomes to be studied, we should gain an understanding of the distribution of CTE and academic course-taking in the NELS sample. Table 1 is a cross-tabulation of whether or not an individual fulfilled a CTE concentration during high school and whether or not he or she fulfilled an academic concentration. The definitions used here for CTE (or, interchangeably, vocational) concentration and academic concentration follow those used in a recent pair of reports from the U.S. Department of Education (National Center for Education Statistics, 1999b , 1999c ). Specifically, in Table 1 and throughout this study, a CTE concentration is defined as having earned at least 3 credits (Carnegie units) in a single Specific Labor Market Preparation (SLMP) vocational area. Those readers familiar with the 1998 revision of the Secondary School Taxonomy may also know the SLMP vocational areas as the "2_C categories" (National Center for Education Statistics, 1999b, 1999c). These SLMP vocational areas are the following:
a. agriculture and renewable resources, b. business, c. marketing and distribution, d. health care, e. public and protective services, f. trade and industry, g. technology and communications, h. personal and other services, i. food service and hospitality, j. child care and education, and k. unidentified subject (limited to course titles "Cooperative education 1," "Vocational cooperative program," "Cooperative training, diversified," "Cooperative education 2," and "Off-campus voc/tech training - unspecified"). Table 1
Cross-Tabulation of Academic Concentration and CTE Concentration, for Public High School Students with Four Years of Transcript Data (n=10,408)*
Academic Concentration CTE Concentration No Yes Total No, did not complete 3985 1971 5956 4E+3SS+3S+3M 38.29 19.94 57.23 66.91 33.09 100.00 51.17 75.25 57.23 Yes, did complete 3804 648 4452 4E+3SS+3S+3M 36.54 6.23 42.77 85.44 14.56 100.00 48.83 24.75 42.77 Total 7789 2619 10408 74.84 25.16 100.00 74.84 25.16 100.00 100.00 100.00 100.00
* format of each cell within the cross-tabulation is:
frequency (number of cases) percent of total percent within row percent within column An academic concentration is defined as having fulfilled a somewhat lenient version of the 'New Basics'-four Carnegie units of English and three Carnegie units each of mathematics, science, and social studies. (This is called a "somewhat lenient version" of the New Basics because descriptions of the New Basics sometimes include requirements for computer studies and foreign language, in addition to English, mathematics, science, and social studies). These definitions of CTE and academic concentrations have a basis in previous educational writing and research. The concept of the New Basics was first articulated in the influential report A Nation at Risk (National Commission on Excellence in Education, 1983 ). The New Basics have subsequently had a strong influence on high school curricular policies and have been the subject of some research (e.g., Alexander & Pallas, 1984 ).
Note that Table 1 includes only public high school students and only those sample members for whom four years of transcript data were available. The thresholds defined for CTE and academic concentrations are levels that generally will be reached only cumulatively, over an entire high school career. Thus, neither dropouts nor sample members with incomplete transcript data are represented in Table 1. In fact, for the analyses of dropping out later in this article, we will need to introduce a different technique to represent the balance of CTE and academic course-taking.
Table 1 shows that, of 10,408 weighted cases, 38.29% had completed neither a CTE concentration nor an academic concentration during four years of high school. Supplemental analyses (not shown here) confirm that all of these individuals completed some courses in the core academic areas, and some of these individuals completed some CTE courses, but neither of the thresholds defining concentrations was met.
Just under 19% of the sample members (n=1,971) completed a CTE concentration but not an academic concentration. A larger group, 36.54% of the sample, fulfilled an academic concentration but not a CTE concentration. Finally, a relatively small group (6.23% of the sample) -but one that is very important to our analyses-fulfilled both CTE and academic concentrations. This distribution of cases across the four cells of Table 1 is generally consistent with patterns reported elsewhere-based on both NELS and other nationally representative samples-for U.S. high school students in the first half of the 1990s (Levesque et al., 2000 ; National Center for Education Statistics, 1999a ).
Table 2 summarizes eighth-grade achievement levels, gender and racial composition, and socioeconomic status (SES) for students in each of the four categories established in Table 1. The variable measuring socioeconomic status is a composite of parents' education, parents' occupational prestige, and family income. It is named "F2SES1" in the NELS database. Details on its construction can be found in "Appendix H" of Ingels et al. (1994) .
Table 2
Mean 8th Grade Test Scores, Gender Composition, Racial Composition, and Socioeconomic Status, by Cross-Classification of CTE Concentration and Academic Concentration, for Public High School Students with Four Years of Transcript Data (n=10,408)
CTE (no),
Acad (no)CTE (yes),
Acad (no)CTE (no),
Acad (yes)CTE (yes),
Acad (yes)8th grade mathematics mean 34.3 31.7 41.5 37.9 8th grade science mean 18.4 17.2 20.7 19.6 8th grade reading mean 26.2 23.6 30.7 27.4 8th grade history mean 29.2 28.0 31.4 30.0 Male (proportion) 0.48 0.58 0.46 0.55 Asian (proportion) 0.033 0.026 0.048 0.029 Hispanic (proportion) 0.116 0.111 0.075 0.076 Black (proportion) 0.120 0.123 0.112 0.116 Native American (proportion) 0.012 0.013 0.006 0.011 White or other (proportion) 0.719 0.728 0.760 0.768 SES (composite mean) -0.080 -0.306 0.254 -0.056 The four columns of Table 2 correspond to the four cells of Table 1. Across the four subject areas tested in eighth grade (mathematics, science, reading, and history), a consistent pattern is revealed. That is, those who would become purely academic concentrators in high school consistently scored the highest on the eighth-grade tests, followed by those who would be dual concentrators, followed by those who would concentrate in neither area. Finally, the purely CTE concentrators had the lowest average test scores in each subject area. These differences in pre-high school achievement levels alert us to the fact that prior achievement should be controlled statistically in our predictive models of high school achievement and persistence. Similarly, the four groups differ enough in terms of gender composition, racial composition, and socioeconomic status to require that we control for these variables in our multivariate models.
1992 Test Performance
We begin our examination of the multivariate models by considering 1992 test performance in four core academic subject areas. Tables 3 through 6 show estimated regression coefficients for models of 1992 achievement on standardized tests of mathematics, science, reading, and history, respectively. Each table summarizes four estimated models which add predictors successively, building to the final models (Model 3D in Table 3, Model 4D in Table 4, Model 5D in Table 5, Model 6D in Table 6). Each table's Model A includes just an intercept and a prior test score from eighth grade. Each Model B adds dummy variables indicating gender and race/ethnicity. Each Model C adds socioeconomic status as a predictor. Having entered these background controls, each of which has quite consistently proven to be correlated with academic achievement in the cumulative body of education research and in these models of Tables 3 through 6, we can focus on the effects of CTE and academic course-taking in each Model D.
Three dummy variables and an excluded reference category are used to indicate an individual's balance of CTE and academic course-taking. The first of these dummy variables included in the models is "CTE (no), Acad (no)," which takes the value "1" if an individual fulfilled neither concentration; it takes the value "0" otherwise. The second dummy variable is "CTE (yes), Acad (no)," which takes the value "1" for individuals who were purely CTE concentrators; it takes the value "0" otherwise. Finally, the third dummy variable is "CTE (yes), Acad (yes)," which equals "1" for dual concentrators and equals "0" otherwise. The excluded reference category represents purely academic concentrators.
For each of the four subject areas (in each of Tables 3 through 6), the block of three dummy variables improves the fit or explanatory power of the model, as measured by improvements in adjusted R2 statistics. Over and above the background control measures introduced in the earlier models, the course-taking indicators of each Model D have significant associations with student achievement. While these models are not growth models, per se, they are models of 1992 achievement that control for 1988 achievement. Thus, we can interpret the coefficients as estimated differences in 1992 achievement for two hypothetical individuals who shared the same pre-high-school achievement levels, gender, race, and SES, but who differed in their high school course-taking trajectories.
Table 3
OLS Regression Models of 1992 Mathematics Achievement (n=8,570)
  Model 3A 3B 3C 3D Intercept 13.31*** 14.07*** 15.18*** 19.52*** 8th grade
math test0.96*** 0.94*** 0.91*** 0.86*** Male 0.86*** 0.78*** 1.14*** Asian 2.05*** 2.00*** 1.71*** Hispanic -1.10*** -0.31 -0.56 Black -2.74*** -2.26*** -2.75*** Native American -2.74** -2.31** -2.23** SES 1.56*** 1.01*** CTE (no),
Acad (no)-3.77*** CTE (yes),
Acad (no)-5.71*** CTE (yes),
Acad (yes)-0.91** Adjusted R² 0.671 0.677 0.683 0.706 * p <.05 ** p <.01 *** p <.001Table 4
OLS Regression Models of 1992 Science Achievement (n=8,511)
  Model 4A 4B 4C 4D Intercept 6.25*** 7.38*** 8.11*** 9.80*** 8th grade
science test0.90*** 0.84*** 0.80*** 0.76*** Male 1.13*** 1.12*** 1.28*** Asian 0.03 -0.04 -0.19 Hispanic -1.40*** -0.80*** -0.89*** Black -2.74*** -2.34*** -2.52*** Native American -1.98*** -1.61*** -1.57*** SES 1.10*** 0.87*** CTE (no),
Acad (no)-1.44*** CTE (yes),
Acad (no)-1.99*** CTE (yes),
Acad (yes)-0.60** Adjusted R² 0.494 0.524 0.539 0.554 * p <.05 ** p <.01 *** p <.001For each of four subject areas, the rank ordering of the four course-taking categories-in terms of estimated effects on achievement-is the same. Specifically, the purely academic concentrators are estimated to show the highest achievement. Significantly behind this group, but ranked second, are the dual concentrators. Ranked third is the group that fulfilled neither concentration. The lowest-ranked group, in terms of estimated achievement, is the group of purely CTE concentrators.
To illustrate the case of mathematics, parameter estimates in the final column of Table 3 reveal that dual concentrators are estimated to score 0.91 points behind the purely academic concentrators. Those who fulfilled neither concentration are estimated to score 3.77 points behind the purely academic concentrators (and 2.86 points behind the dual concentrators, which is not shown in the table but can be computed directly from the tabulated coefficients). The purely CTE concentrators are estimated to score 5.71 points behind the academic concentrators, 4.80 points behind the dual concentrators, and 1.94 points behind those who fulfilled neither concentration. To reiterate, these effects of course-taking patterns are estimated after controlling for 1988 test performance and the other variables in the models.
The asterisks indicating significance levels show that each of the three course-taking statuses represented by the included dummy variables ranks significantly behind the academic concentrators. Results of additional t-tests (not shown) confirm that every pair of statuses is significantly differentiated in these models for each of the subject areas. In reporting these significance levels, it is important to compare the findings with results reported in the recent report by Levesque and her colleagues ( 2000 ). Those analysts presented descriptive tables that compared mean growth in mathematics and reading between 1988 and 1992 for various subgroups derived from this same NELS data set. They used a course-taking categorization of (a) college preparatory only, (b) vocational concentration only, (c) both vocational concentration and college preparatory, and (d) other/general that very nearly corresponds to the categorization used in this article's models. For gains between 1988 and 1992, they found the same rank ordering among the course-taking categories that is being reported here. However, their comparisons of subgroup means showed that the differences between the college preparatory group and the dual concentrators were statistically insignificant, or indistinguishable.
It appears that the discrepancy in significance levels between the two analyses has to do with the difference between estimating multiple regression models and comparing subgroup means in descriptive tables. With a sample as large as we have available in the present analyses, even fairly small regression coefficients can prove to be statistically significant. In addition to assessing statistical significance, then, one should consider substantive significance.
Table 5
OLS Regression Models of 1992 Reading Achievement (n=8,569)
  Model 5A 5B 5C 5D Intercept 10.67*** 12.23*** 12.99*** 15.04*** 8th grade
reading test0.83*** 0.80*** 0.77*** 0.73*** Male -0.67*** -0.79*** -0.67*** Asian 1.14** 1.05** 0.84* Hispanic -1.02*** -0.43 -0.57* Black -2.80*** -2.40*** -2.61*** Native American -2.47** -2.14** -2.10** SES 1.12*** 0.82*** CTE (no),
Acad (no)-1.61*** CTE (yes),
Acad (no)-2.99*** CTE (yes),
Acad (yes)-0.62* Adjusted R² 0.514 0.524 0.530 0.540 * p <.05 ** p <.01 *** p <.001Appendix Table A1 shows descriptive statistics for the variables and samples of Tables 3 through 6. From this appendix table, we can see that 1992 mathematics achievement for this sample had a mean of 48.953 and a standard deviation of 13.688. In light of these facts, what should we make of the estimated difference between the academic concentrators and the dual concentrators of 0.91 test score points? Well, at some level the difference simply is what it is; 0.91 divided by 13.688 is about 0.07, which would generally be deemed a fairly modest effect. For each of the other subject areas, this version of an effect size is of a similar magnitude. It seems sensible to conclude that the dual concentrators definitely lagged behind the purely academic concentrators in achievement growth, but not by especially large margins.
Table 6
OLS Regression Models of 1992 History Achievement (n=8,452)
  Model 6A 6B 6C 6D Intercept 11.20*** 12.24*** 13.35*** 15.10*** 8th grade
history test0.80*** 0.77*** 0.73*** 0.69*** Male 0.25** 0.25** 0.40*** Asian 0.31 0.25 0.12 Hispanic -0.92*** -0.42** -0.50*** Black -1.75*** -1.39*** -1.49*** Native American -1.52*** -1.26** -1.25** SES 0.89*** 0.70*** CTE (no),
Acad (no)-1.08*** CTE (yes),
Acad (no)-1.82*** CTE (yes),
Acad (yes)-0.65*** Adjusted R² 0.465 0.478 0.492 0.507 * p<.05 ** p<.01 *** p<.001What might explain this advantage for the academic concentrators, and the differences among the four course-taking trajectories more generally? A small part of the explanation may be revealed by Table 7. This table shows mean Carnegie credits earned in various curricular areas during the high school career for students from each of the four course-taking categories. In this table, higher mathematics includes geometry, Algebra 2 through pre-calculus, and courses classified as advanced mathematics (calculus, AP/IB courses, and a few other courses including SAT review, actuarial sciences, and matrix algebra)-courses classified as "higher mathematics" are those listed in the 1998 revision of the Secondary School Taxonomy under 1_15, 1_16, and 1_17 (National Center for Education Statistics, 1999c ). Higher science includes regular, advanced, honors, and specialized courses in biological sciences; regular, advanced, honors, and specialized courses in chemistry; and regular, advanced, honors, and specialized courses in physics-courses classified as "higher science" are those listed in the 1998 revision of the Secondary School Taxonomy under 1_22B, 1_22C, 1_22D, 1_23B, 1_23C, 1_23D, 1_24B, 1_24C, and 1_24D (National Center for Education Statistics, 1999c ).
From Table 7, one can see that the purely academic concentrators and the dual concentrators were fairly similar in the amount of total mathematics, total science, English, and social studies they completed during their high school years, on average. For each of these subject groupings, the means for the academic concentrators and dual concentrators are within 0.2 Carnegie units of one another. In higher mathematics and higher science, however, the academic concentrators distanced themselves from the dual concentrators slightly more. In higher mathematics, for example, the academic concentrators completed 2.5 Carnegie units, on average, during their high school careers while the dual concentrators completed only 2.1 credits. This difference of just under a semester's worth of higher mathematics course-taking may begin to explain the differential achievement effects estimated in Table 3.
As we examine Table 7, we should understand a likely reason for the discrepancy in higher mathematics and higher science credits: The dual concentrators were (partly, by definition) completing much more CTE course-taking during their high school careers than were the academic concentrators. The dual concentrators completed 6.5 units of career and technical education while the academic concentrators completed only 2.4 units of CTE. Given the finite amount of time in a student's course schedule each semester, the relatively high levels of CTE course-taking among dual concentrators would have necessarily cut into some other potential course-taking. Apparently, for many of these dual concentrators, advanced topics in mathematics and science are a part of what received diminished priority.
Table 7
Mean Course Credits in Various Areas During High School Career, by Cross-Classification of CTE Concentration and Academic Concentration, for Public High School Students with Four Years of Transcript Data (n=10,408)
CTE (no),
Acad (no)CTE (yes),
Acad (no)CTE (no),
Acad (yes)CTE (yes),
Acad (yes)All mathematics 2.9 2.6 3.8 3.7 Higher mathematics 1.2 0.7 2.5 2.1 All science 2.4 2.1 3.7 3.6 Higher science 1.4 1.0 2.6 2.2 English 4.0 4.0 4.4 4.4 Social Studies 3.4 3.1 3.8 3.6 CTE 3.4 7.0 2.4 6.5 Table 8
Maximum Likelihood Estimates of Effects on Log-Odds of Dropping Out of High School (n=11,352)
  Model 8A 8B 8C 8D 8E 8F Intercept -1.97*** -1.99*** -2.11*** 1.98*** 3.19*** 3.62*** Male -0.13* -0.09 -0.57*** -0.57*** -0.58*** Asian -0.43* -0.46* -0.08 -0.19 -0.20 Hispanic 0.49*** -0.09 -0.31** -0.46*** -0.45*** Black 0.22** -0.23* -0.85*** -1.05*** -1.06*** Native American 0.88*** 0.44 -0.07 -0.28 -0.30 SES -0.93*** -0.59*** -0.69*** -0.70*** 8th grade tests -0.02*** -0.03*** -0.03*** High school GPA -1.83*** -1.91*** -1.89*** CTE/Acad ratio -2.06*** -4.57*** (CTE/Acad ratio)² 2.97*** -2 log-likelihood 8415.47 8354.79 7862.48 6434.93 6243.92 6203.90 Improvement in Chi-Square 60.67 552.99 1980.54 2171.55 2211.57 Degrees of freedom 5 6 8 9 10 Percent concordant 44.4 68.1 84.4 85.1 85.2 c statistic .569 .685 .846 .852 .854 * p <.05 ** p <.01 *** p <.001To summarize the analyses of 1992 test performance in the four core academic subjects, there is a small but statistically significant effect of choosing to pursue two concentrations in high school. Even if there are some motivational benefits associated with a dual concentration for some students, the zero-sum nature of time in a student's course-taking schedule may partially explain the fact that purely academic concentrators exhibited higher 1992 achievement levels-controlling for 1988 achievement-than did dual concentrators. Additionally, there may be other important differences in the nature and quality of instruction for the two groups that have not been explicitly modeled in these analyses as well as other unmeasured differences between these students. Any such differences merit future research attention.
Dropping Out of High School
Table 8 summarizes logistic regression models of the log-odds of dropping out of high school prior to graduation (at any point between March, 1989, and the spring of 1992). Appendix Table A2 shows descriptive statistics for the variables and cases of Table 8. That appendix table shows that, overall, 12.28% of this public school sample dropped out of high school at some point. (Some of these dropouts later returned to pursue high school completion; this dependent variable literally measures whether the individual "ever dropped out" between 1989 and 1992.)
Similar to what was presented for 1992 test scores, a series of models is built successively across the columns of Table 8, culminating in the final Model 8F. The preliminary models introduce an intercept, dummy variables for gender and race/ethnicity, a measure of SES, an eighth-grade test score composite measure, and high school grade point average. Grade point average is calculated from transcript data and, in the case of dropouts, is calculated based on grades earned during the time the individual was enrolled in high school.
Two variables-different from the dummy variables used in Tables 3 through 6-capture an aspect of the balance between CTE and academic course-taking for the models of Table 8. In Model 8E, the ratio of CTE credits earned to academic credits earned is entered as a predictor. In constructing this CTE/academic ratio variable, CTE courses include all courses listed under 2_A, 2_B, and 2_C in the 1998 revision of the Secondary School Taxonomy. Academic courses include all mathematics, science, English, and social studies (including history) courses; these are all courses listed under 1_1, 1_2, 1_3, and 1_4 in the 1998 revision of the Secondary School Taxonomy (National Center for Education Statistics, 1999c ). For this particular analysis, this predictor is preferable to a series of dummy variables such as those used in Tables 3 through 6 because of censoring issues. As was stated earlier, the thresholds defined for CTE and academic concentrations in the models of academic achievement are levels that generally could be reached only cumulatively, over an entire high school career. For dropouts, the high school career is by definition truncated before graduation. Thus, we would expect few or no dropouts to have exceeded the New Basics threshold or-most likely-the CTE concentration threshold. The use of the CTE/academic ratio is intended as a solution to the censoring problem. Regardless of how many high school semesters a student completed-perhaps 2 or 4 or 5 for an eventual dropout, generally 8 for an on-pace graduate-the ratio of CTE credits to academic credits can be calculated.
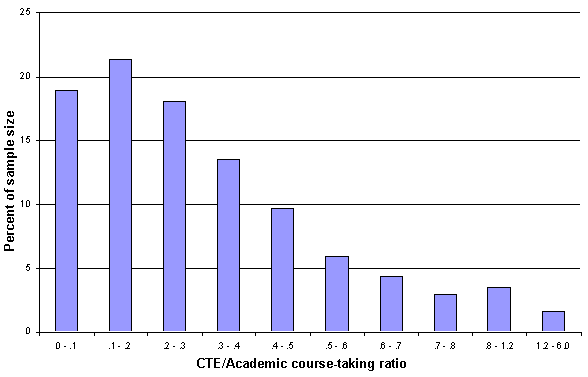
The research question of interest is this: Is there a significant relationship between this CTE/academic ratio and an individual's likelihood of dropping out? Figure 1 shows the distribution of CTE/academic ratio levels for this sample. The histogram illustrates that just under 19% of the sample had ratios between 0 and 0.1. Another 21.36% had ratios between 0.1 and 0.2. Cumulatively, 81.61% had ratios somewhere below 0.5, which is the point at which an individual is taking one CTE course for every two academic courses.
Figure 1 is presented partly to illustrate the small but noteworthy number of cases in the right-hand tail of the distribution. Approximately 1.6% of the cases have ratios between 1.2 and 6.0. A more detailed examination of the distribution suggested that, substantively and empirically, a distinct breakpoint exists in the data somewhere around 1.2. Cases with ratios above this level are truly special cases. These are probably either individuals in very specialized vocational academies or individuals with transcript data of questionable accuracy. In either case, their extreme values on this important explanatory variable give these cases the potential to have undue influence on model estimation. It is probably best to eliminate them from the analyses.
Accordingly, the analyses of Table 8 are limited to cases with CTE/academic ratios between 0 and 1.2. Interpretations of the model estimations should not be extended to cases with values above 1.2. Even at levels between 0.8 and 1.2, we should make inferences with some caution due to the sparseness of the data in this range.
There are interesting and important findings regarding gender, race, and SES in the models that precede Model 8E. Some of these findings are best understood by reading across the models of Table 8. Most notable, perhaps, is the way black and Hispanic students are shown to be significantly more likely to drop out than white students in Model 8B, but then significantly less likely to drop out than white students in later models. The change in direction of association appears and becomes more pronounced as SES, prior achievement, and high school GPA are introduced in succession. A likely explanation, or interpretation, of the changes across successive models is that the high dropout rates observed for black and Hispanic students in the sample-before controlling for various background characteristics-are driven by the relatively low levels of SES and scholastic achievement that characterize these groups on average. Their low levels of SES and achievement place them at relatively high risk for dropping out. If we compare black, Hispanic, and white students at common (shared) levels of SES and scholastic achievement, however, the black and Hispanic students are at lower risk than their white counterparts for dropping out. On one hand, this interpretation highlights a distressing situation for black and Hispanic students, as their lesser socioeconomic resources and educational disadvantages have serious consequences for their life-course trajectories. On the other hand, this interpretation also could prompt one to ask about positive messages or influences regarding persistence in school being received by black and Hispanic students of a given socioeconomic status and achievement level-relative to white students of the same SES and achievement level. These interesting and important findings are not given further attention here, in the interest of article length and focus, but they certainly merit future investigation.
Figure 1. Distribution of CTE/Academic course-taking ratio, for public high school students including dropouts (n=12,303)
Let us return more directly to the estimated models of Table 8. By entering the CTE/academic ratio as a first-order effect in Model 8E, we are testing whether there is a linear relationship (whether positive or negative in sign) between the CTE/academic ratio and the log-odds of dropping out. And, in fact, a negative and significant relationship is estimated (See coefficient of -2.06.). Model 8E does offer a significant improvement in fit over each of Models 8A through 8D. The substantive implication of Model 8E is that, if we constrain the relationship between the CTE/academic course-taking ratio and the log-odds of dropping out to be linear, a greater representation of CTE courses in an individual's high school experience reduces the likelihood of dropping out. This finding is tentative support for the idea that a coupling of career-related courses with an academic load may increase a student's commitment or attachment to high school.
Before we go too far with this interpretation, however, we should consider Model 8F. In this model a squared term is added as a predictor. This polynomial functional form allows us to investigate whether a significant curvilinear relationship exists between the CTE/academic ratio and dropping out. With this functional form, we can ask: Is too much CTE too much of a good thing? Is there a point of inflection, after which the risk of dropping out begins to rise?
Figure 2. Predicted log-odds of dropping out, as "CTE/Academic course-taking ratio" varies, for a white male of average family SES
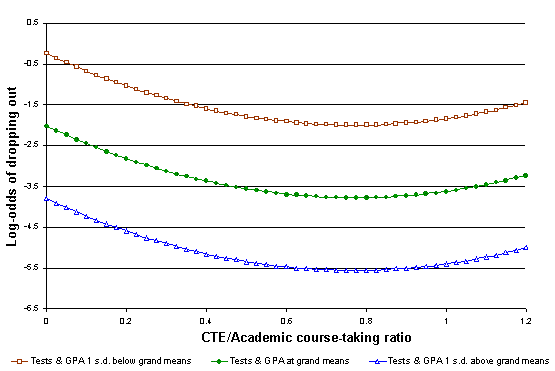
Model 8F suggests that indeed there is a significant curvilinear relationship between the probability of dropping out and the ratio of CTE credits to academic credits. Specifically, controlling for prior achievement, grades, and student background characteristics, a student's probability of dropping out appears to be lowest when approximately 3 Carnegie units of CTE are completed for every 4 Carnegie units of academic subjects. That is, the point of inflection for this polynomial function comes when the CTE/academic ratio is about 0.77. This is the point at which the risk of dropping out is estimated to be at its lowest.
To help us visualize the nature and magnitude of this effect, Figure 2 depicts predicted log-odds of dropping out for three hypothetical sets of students, as the CTE/academic ratio ranges from 0 to 1.2. All three curves in the figure are plotted using the estimated coefficients of Model 8F, and for white males of average SES. Distinguishing the curves beyond those commonalities, however, are the facts that the top curve plots estimates for individuals whose eighth-grade test scores and high school grade point average were both one standard deviation below the sample's grand means. The middle curve plots estimates for individuals who were at the sample means for test scores and grade point average. The lowest curve represents individuals whose tests and grade point average were one standard deviation above the grand means.
The fact that the individuals with above-average tests and grade point averages have the lowest log-odds of dropping out (the most negative log-odds) reflects the fact that higher test scores and grades provide a buffer against the risk of dropping out. The shapes of the three curves in Figure 2 are the same. What differs are their orientations along the vertical axis. These differences are driven by their differing test scores and grades. Movement up or down the CTE/academic ratio scale affects all three hypothetical populations equally in terms of log-odds.
In terms of estimated probabilities of dropping out, however, a more complex and intriguing pattern exists. Figure 3 presents predicted probabilities of dropping out, for the same hypothetical populations as were depicted in Figure 2 and across the same range of CTE/academic ratios. Again, the plotted curves of Figure 3 are derived from the parameter estimates of Model 8F, with appropriate mathematical transformations completed to express outcomes in terms of probabilities rather than log-odds.
Figure 3 reflects the fact that a fixed change in the CTE/academic ratio has a greater effect on the probability of dropping out when we are considering a set of individuals whose other risk factors place their overall probability of dropping out near the middle of its possible range (approaching 0.5) rather than near 0 or 1 (Agresti, 1990 , p. 84). This fact is inherent in the properties of logistic regression and does not represent an interaction term, per se, as some might be tempted to claim. For example, we are not witnessing an interaction between the CTE/academic ratio and grade point average as these variables affect the log-odds of dropping out. Rather, we are witnessing the fact that a unit change in the log-odds of dropping out implies a greater change in the probability of dropping out when the probability of dropping out is near the middle of its possible range rather than being near 0 or 1.
Figure 3. Predicted probability of dropping out, as "CTE/Academic course-taking ratio" varies, for a white male of average family SES
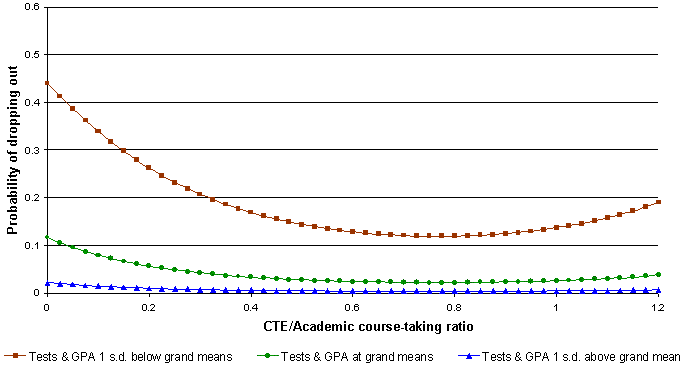
Let us not get lost in these methodological details, however, but instead let us focus on the substantive implications of Model 8F, and Figures 2 and 3. Substantively, the estimated model implies that there is a healthy middle-range mix of CTE and academic course-taking that may maximize students' attachment and perseverance in high school. The implications of this curvilinear trend are most salient for students who are already at relatively high risk of dropping out (due to low prior test scores or low grades, for example). For these students, especially, it may be that a high school experience that is purely academic presents them with courses that do not seem highly relevant to their goals or worldviews. Further it is possible (but not investigated in the present analyses) that a high school experience that is purely academic but aimed at students whose achievement levels place them at low or middle-range levels may be characterized by unengaging, watered-down versions of more challenging and inspiring courses offered to higher achieving students.
If the preceding paragraph offers possible explanations for the left-hand part of the curvilinear function (for CTE/academic ratios between 0 and 0.77), how might we explain the estimated effects for the right-hand part of the function (as CTE/academic ratios grow beyond 0.77)? As we approach this other end of the CTE/academic ratio distribution, it appears that a high school experience that tips too far toward career and technical education, to the exclusion of a solid academic grounding, also increases the risk of dropping out. We can speculate that this finding might be due to educational experiences that are relegating students to the periphery of the high school's culture and mission. Further investigations are warranted to discover more about why a certain middle-range mix of CTE and academic course-taking may minimize the frequency of students dropping out.
As a final point on the analyses of dropping out, readers might be curious about whether the relationship between the CTE/academic ratio and the likelihood of leaving school varies for different racial or ethnic groups. Relatedly, some might wonder what Figures 2 and 3 would look like if plotted for, say, Hispanic or black students instead of white students. Several things can be said about these topics.
First, as Model 8F is specified, there are no interaction terms between the race/ethnicity indicators and the first-order or squared terms representing the CTE/academic ratio. Therefore, based on this model, a plotting of Figure 2 for black or Hispanic students instead of white students would simply show the three plotted curves shifted further down the figure's vertical axis (refer back to Table 8 and the explanation on gender and race for Table 8 above to review the fact that black and Hispanic students are estimated to have a lower likelihood of dropping out than white students once SES and academic achievement are statistically controlled). The shape of the curves-and the distance between curves defined by varying grades and prior test scores-would remain as they appear in the current Figure 2. Based on Model 8F, a plotting of the probability of dropping out-that is, the translation to a plotting of Figure 3-for black or Hispanic students would still show a point of inflection at 0.77, and functions that were more dramatically curved for students with low grades and prior test scores than for students with high grades and prior test scores. So, in summary, based on the current Model 8F, the estimated relationship between the CTE/academic ratio and the likelihood of dropping out holds uniformly for all racial or ethnic groups (and, by the same logic, for groups defined by gender or SES).
Would our statistical models fit the data better-and tell a more accurate story-if they included interaction terms between the race/ethnicity indicators and the first-order or squared terms representing the CTE/academic ratio? To address this question, several alternate model specification were tried (but are not shown in Table 8). When interaction terms between race/ethnicity and the first-order CTE/academic ratio effect were added to Model 8E, these interaction terms were not statistically significant; the expanded model did not offer a significant improvement in fit over Model 8E.
When interaction terms between the race/ethnicity indicators and both first-order and squared CTE/academic ratio variables were added to Model 8F, there was a slight improvement in goodness-of-fit. There was some suggestion that the relationship between the CTE/academic ratio and the likelihood of leaving school was somewhat different for blacks and Hispanics, as compared to whites. Specifically, the estimated coefficients suggested that the point of inflection (the mix of CTE and academic course-taking that minimized the likelihood of dropping out) was located at lower point on the CTE/academic ratio scale for blacks and Hispanics, as compared to whites. The estimated coefficients also suggested that the functions (as plotted in Figures 2 and 3) were more dramatically concave for blacks and Hispanics than for whites. However, it seems unwise to give these interaction terms much credence due to sparseness of data at the upper extremes of the CTE/academic ratio scale. Specifically, once we disaggregate by race/ethnicity, problems of sparse data at the upper extremes of this scale become amplified.
Examining unweighted cases within the data set, only 52 of 1,065 black students had CTE/academic ratios above 0.7. The comparable numbers were 66 of 1,368 for Hispanic students, 11 of 722 for Asian students, 6 of 113 for Native American students, and 583 of 8,084 for white students. These small numbers of cases at the high end of the CTE/academic ratio scale make it very problematic to estimate separate polynomial functions for each racial or ethnic group. Each case at the high end of the scale is potentially a very influential outlier, and the resultant estimates of polynomial functions are very unstable or suspect in the sense that different outcomes for just a few students would have dramatically changed the estimated functions. This is a case where there is probably safety in numbers: When we draw upon the strength of all racial and ethnic groups combined, to estimate a single polynomial function as in Model 8F, we can probably have a fair amount of confidence in the estimate. Based on this data set and its distribution of cases it seems unwise to trust polynomial functions estimated separately for each racial or ethnic group. Investigation of differing curves for various racial or ethnic groups should wait for a different, purposively selected, sample.
Conclusions
This study has examined the balance struck between CTE and academic course-taking during the high school years for members of a nationally representative sample of individuals who were eighth graders in the United States in 1988. Further, the study has examined the relationship of this CTE/academic balance with (a) test scores and (b) the likelihood of dropping out. The balance between CTE and academic course-taking appears to have some influence on both outcomes.
This study found that dual and academic concentrators differed only slightly on standardized tests of mathematics, science, reading, or history. The small, but statistically significant, advantage enjoyed by purely academic concentrators may be partly attributable to the additional coursework in advanced subjects. These analyses suggest that a middle-range integration of CTE and academic scheduling has significant potential to reduce the likelihood of dropping out. Specifically, a ratio of approximately three CTE credits to every four academic credits was associated with the lowest likelihood of dropping out. Figure 3 showed that this finding is especially salient for individuals who are otherwise at risk of dropping out-due to low prior grades, or low prior test scores, or other risk factors.
If a middle-range mix of CTE and academic course-taking can lower the risk of dropping out for some students, educators and policymakers might be wise to encourage such a mix, even if it brings slight reductions in standardized test scores in core academic subjects. Given the importance of a high school diploma in our society, slight reductions in test scores might be found acceptable in exchange for higher graduation rates.
This article raises several issues deserving of further investigation. For example, even if these analyses have convinced us of the benefits of a middle-range mix of CTE and academic course-taking for some students, many unanswered questions remain about the best ways to integrate CTE and academic offerings. The current National Assessment of Vocational Education (NAVE) is attempting, among its other goals, to assemble case studies and qualitative accounts based on effective programs that integrate academic and vocational education. Important questions include the following: Within integrated programs, are students' academic and motivational outcomes affected by the extent to which their teachers of CTE and academic courses prepare lessons and teach in close collaboration with one another? What are some of the most effective ways for teachers of academic subjects to illustrate linkages between their subjects and career applications? How can CTE teachers forge explicit connections to the academic subjects in their instruction? What sorts of professional development or specialized training do teachers need to support their attempts at integrating academic and vocational education?
It will also be important to attempt to replicate-and build upon-the findings we have generated from the NELS data with more recent data. The NELS subjects attended high school just as the 1990 Perkins Act was beginning to affect the organization of secondary education. Would cross-tabulations of CTE and academic course-taking from the late 1990s or the first years of the 21st Century look similar to those from the early 1990s? Would associations between the CTE/academic balance and (a) test scores or (b) the likelihood of dropping out remain stable? Or have changes occurred? If changes have occurred, can these be traced to influences of the 1998 Perkins Act, with its further encouragement of academic and vocational integration?
Finally, if we accept this article's suggestions about the curvilinear relationship between the CTE/academic balance and the likelihood of dropping out, many questions arise about why course sequences that are too heavy in either academics or CTE are associated with relatively high rates of school-leaving. Are students at the two extremes of the continuum experiencing pushes away from high school or pulls toward non-high school endeavors (Gambetta, 1987 )? Is it true that, for students who are already at relatively high risk of dropping out, a high school experience that is purely academic offers courses that do not seem highly relevant to their goals or worldviews? Is it the case that a high school experience that is purely academic but aimed at students with low or middle-range achievement is often characterized by unengaging, diluted versions of more challenging and inspiring courses offered to higher achieving students?
At the other extreme, what characteristics of a high school experience that focuses too exclusively on career and technical education seem to increase the risk of dropping out? Is such a CTE-intensive experience convincing students that they should join the world of full-time paid employment as soon as possible, even if this entails leaving high school prior to graduation? Are a substantial number of students who concentrate heavily in CTE already somewhat disengaged from formal education before the high school years? Do they seek CTE courses in an effort to find their niche within larger high schools, but find that even this niche does not bring the rewards they are seeking? Or is a student's "seeking" not even the relevant part of the phenomenon to explore? Rather, should we focus our attention on the ways that adults and guidance systems within high schools sort and place students, separate from the students' preferences and decisions?
The preceding paragraphs have posed many questions. Most of these are not questions addressed by the present study, but rather are prompted by the study's findings. It would be premature to make strong policy recommendations based on the findings of this research. But, clearly, with the current NAVE, the work of the National Research Center for Career and Technical Education, and many state and local initiatives, we are in the midst of ongoing debate and investigation into the ways that CTE and academic education can best be integrated. It is hoped that this study has offered some new information to this debate, and that future research will provide answers to many of the remaining questions.
References
Agresti , A. (1990). Categorical data analysis . New York: John Wiley & Sons.
Alexander , K. L., & Pallas, A. M. (1984). Curriculum reform and school performance: An evaluation of the "New Basics." American Journal of Education , 92, 391-420.
Boesel , D., & McFarland, L. (1994). National Assessment of Vocational Education, Final report to Congress . Volume I: Summary and recommendations. Washington, DC: U.S. Government Printing Office.
Boesel , D., Hudson, L., Deich, S., & Masten, C. (1994). National Assessment of Vocational Education, Final report to Congress . Volume II: Participation in and quality of vocational education. Washington, DC: U.S. Government Printing Office.
Crain , R. L., Allen, A., Little, J. W., Sullivan, D., Thaler, R., Quigley, D., & Zellman, G. (1998). The effects of career magnet schools (IEE Brief Number 22). New York: Columbia University, Teachers College, Institute on Education and the Economy,.
Crain , R. L., Allen, A., Thaler, R., Sullivan, D., Zellman, G., Little, J. W., & Quigley, D. D. (1999). The effects of academic career magnet education on high schools and their graduates (MDS-779). Berkeley, CA: University of California, National Center for Research in Vocational Education,.
Delci , M., & Stern, D. (1999). Who participates in new vocational programs? A preliminary analysis of student data from NLSY97 . Berkeley, CA: University of California, National Center for Research in Vocational Eduation,.
Gambetta , D. (1987). Were they pushed or did they jump? Individual decision mechansisms in education . New York: Cambridge University Press.
Garet , M. S., & DeLany, B. (1988). Students, courses, and stratification. Sociology of Education , 61, 61-77.
Hallinan , M. T. (1994). Tracking: From theory to practice. Sociology of Education , 67, 79-84.
Hoachlander , E. G., Kaufman, P., Levesque, K., & Houser, J. (1992). Vocational education in the United States: 1969-1990 (NCES 92-669). Washington, DC: U.S. Department of Education., U.S. Government Printing Office.
Ingels , S. J., Abraham, S. Y., Spencer, B. D., & Frankel, M. R. (1989). National Education Longitudinal Study of 1988. Base year: Student component data file user's manual . Washington, DC: U.S. Department of Education, Office of Educational Research and Improvement.
Ingels , S. J., Dowd, K. L, Baldridge, J. D., Stipe, J. L, Bartot, V. H., & Frankel, M. R. (1994). National Education Longitudinal Study of 1988. Second follow-up: Student component data file user's manual . Washington, DC: U.S. Department of Education, Office of Educational Research and Improvement.
Levesque , K., Lauen, D., Teitelbaum, P., Alt, M., & Librera, S. (2000). Vocational education in the United States: Toward the Year 2000 (NCES 2000-029). Washington, DC: U.S. Department of Education.
Levesque , K., Premo, M., Vergun, R., Emanuel, D., Klein, S., Henke, R., Kagehiro, S., & Houser, J. (1995). Vocational education in the United States: The early 1990s (NCES 95-024). Washington, DC: U.S. Department of Education, U.S. Government Printing Office.
National Center for Education Statistics . (1996). National Education Longitudinal Study: 1988-94-Data files and electronic codebook system, restricted use [CD-ROM]. Washington, DC: U.S. Department of Education.
National Center for Education Statistics . (1999a). Issue brief: Students who prepare for college and a vocation (NCES 1999-072). Washington, DC: U.S. Department of Education.
National Center for Education Statistics . (1999b). Procedures guide for transcript studies (Working paper no. 1999-05). Washington, DC: U.S. Department of Education.
National Center for Education Statistics . (1999c). 1998 revision of the Secondary School Taxonomy (Working paper no. 1999-06). Washington, DC: U.S. Department of Education.
National Center for Education Statistics . (2000). Stats in brief: Changes in high school vocational coursetaking in a larger perspective (NCES 2001-026). Washington, DC: U.S. Department of Education.
National Commission on Excellence in Education . (1983). A nation at risk: The imperative for educational reform . Washington, DC: U.S. Department of Education.
Oakes , J. (1994). More than misapplied technology: A normative and political response to Hallinan on tracking. Sociology of Education , 67, 84-89.
Oakes , J., Gamoran, A., & Page, R. N. (1992). Curriculum differentiation: Opportunities, outcomes, and meanings. In P.W. Jackson (Ed.), Handbook of research on curriculum (pp. 570-608). Washington, DC: American Educational Research Association.
Powell , A. G., Farrar, E., & Cohen, D. K. (1985). The shopping mall high school: Winners and losers in the educational marketplace . Boston: Houghton Mifflin.
Rasinski , K. A., & Pedlow, S. (1998). The effect of high school vocational education on academic achievement gain and high school persistence: Evidence from NELS:88. In A. Gamoran (Ed.), The quality of vocational education: Background papers from the 1994 National Assessment of Vocational Education (Ch. 5). Washington, DC: U.S. Department of Education.
Rock , D. A., & Pollack, J. M. (1995). Psychometric report for the NELS:88 Base year through Second Follow-Up . Washington, DC: U.S. Department of Education, Office of Educational Research and Improvement.
Acknowledgements
This work was supported by the National Research Center for Career and Technical Education, PR/Award (No. V051A990006) as administered by the Office of Vocational and Adult Education, U.S. Department of Education. However, the contents do not necessarily represent the positions or policies of the funders, and endorsement by the Federal Government should not be assumed. The author thanks James R. Stone III, Sam Stringfield, and Marisa Castellano for insights and advice.
Appendix
Table A1
Percentages, Means, and Standard Deviations for the Variables Used in Models of 1992 Achievement (Tables 3 through 6)*
% Mean S.D. 8th grade (1988) math achievement 36.969 11.633 1992 math achievement 48.953 13.688 8th grade (1988) science achievement 19.256 4.695 1992 science achievement 23.667 6.041 8th grade (1988) reading achievement 27.703 8.480 1992 reading achievement 33.528 9.763 8th grade (1988) history achievement 29.967 4.441 1992 history achievement 35.065 5.187 SES 0.004 0.749 Male 49.50 Female 50.50 White or other 74.33 Asian 3.57 Hispanic 9.54 Black 11.65 Native American 0.91 CTE (no), Acad (no) 37.81 CTE (yes), Acad (no) 17.85 CTE (no), Acad (yes) 37.90 CTE (yes), Acad (yes) 6.44
reading scores (n=8,569, as in Table 5), and history scores (n=8,452, as in Table 6).Table A2
Percentages, Means, and Standard Deviations for the Variables Used in Models of Dropping Out (Table 8) (n=11,352)
% Mean S.D. Ever dropped out 12.28 Never dropped out 87.72 Male 49.18 Female 50.82 White or other 72.48 Asian 3.48 Hispanic 10.24 Black 12.65 Native American 1.15 SES -0.058 0.755 8th grade test composite 50.799 9.797 High school g.p.a. 1.910 0.789 CTE/Acad. ratio 0.297 0.222 (CTE/Acad. ratio)² 0.138 0.198 Author
STEPHEN B. PLANK is Assistant Professor in the Department of Sociology and Research Scientist at the Center for Social Organization of Schools, both at Johns Hopkins University, 3400 N. Charles St., Baltimore, MD 21218. [E-mail: splank@jhu.edu ]. His research interests include peer relations among children, sociological studies of school climate, and the transition to postsecondary education or work.