JVER v28n1 - Applied Technology Proficiency of High School Students in Applied and Traditional Courses
Applied Technology Proficiency of High School Students in Applied and Traditional Courses
Dennis W. Field
Iowa State UniversityAbstract
This investigation compares applied technology skill levels of high school students enrolled in various applied and comparable traditional courses, particularly Principles of Technology and physics courses respectively. Outcomes from ACT's Applied Technology Work Keys ® assessment test were used as a measure of applied technology skill levels. Data were collected on 529 students from intact classes at six Iowa high schools. Multilevel models were used to analyze student, class, and school level data. Group means for grade point averages and Iowa Test of Educational Development scores were higher for students enrolled in physics than for students enrolled in Principles of Technology. Principles of Technology courses appear to be reaching students who may not otherwise have enrolled in traditional physics, and reaching them at an earlier age. Applied Technology test scores were essentially equivalent for students in applied classes as compared to students in corresponding traditional classes when the model includes control variables for gender, GPA, ITED score, and prior coursework in science and mathematics.ParticipantsEmployers are not satisfied with the level of high school graduates' employability skills (e.g., Goldberger & Kazis, 1996 ; ACT Center for Education and Work, 1995 ; Secretary's Commission on Achieving Necessary Skills [SCANS], 1991 ). At the national level, the 1991 SCANS report suggests that employers take a more active role in addressing this problem by telling educators what they need and working with them (p. viii). The fundamental forces, which have been driving the employability skills issue nationally, are also at work at the state level. In Iowa, for example, the Iowa Business Council (IBC)-a non-profit, politically independent group composed of the leadership from approximately 20 major Iowa employers- initiated a project in 1993 that was consistent with SCANS goals. The project sought to improve communications with educators and to quantify both the nature and levels of skills needed by high school graduates to qualify for certain entry-level positions in their member companies.
The IBC project was undertaken with the help of the ACT's Center for Education and Work. ACT has developed a system to quantitatively measure certain employability skills, including skills in the applied technology area where individuals are asked to demonstrate an ability to apply traditional physics concepts to work-related technical problems. The ACT system, Work Keys ® 1 , includes job profiling and work-related assessments, and is designed to serve a variety of needs in both industrial and educational arenas. Educators can use the Work Keys ® information to develop appropriate curricula and instruction that target skills needed in the workplace ( ACT, 1997 ).
Criticisms notwithstanding, a case can be made that educators have long recognized the importance of preparing students for work ( Bennett, 1926 , 1937 ). Educators have been involved in various technical and vocational initiatives, such as School-to-Work and Tech Prep, in an effort to be more responsive to the needs of students, parents, and employers, and to close the gap between education and employability skills. Applied academics 2 , which, according to Hershey, Owens, and Silverberg (1995) is a component of Tech Prep, is one of the initiatives Iowa high schools are pursuing. Roughly 71% of the 362 high schools surveyed in Iowa during the 1995-96 school year offered at least one applied academics course ( Dugger, Lenning, Field, & Wright, 1996 ). While there is favorable anecdotal evidence of the impact of applied academic courses (H. H. Custer, personal communication, August 31, 1995), there appears to be a limited number of studies quantitatively assessing outcomes. Dare (2000) submits that few studies have offered substantial empirical evidence of the effects of applied academics on student learning and of ways in which applied academics benefit learners. She states that there is "little documentation of student outcomes associated with applied academics in the extant literature" (p. 320). Relevant studies that have been conducted compared students enrolled in the applied Principles of Technology (PT) course with students enrolled in traditional academic courses ( Dugger & Johnson, 1992 ; Dugger & Meier, 1994 ; Wang & Owens, 1995 ). Generally favorable results for students enrolled in applied courses versus traditional courses have been reported. Studies by Dugger & Johnson (1992) and Dugger & Meier (1994) described higher levels of student achievement on technology achievement tests by PT students than by traditional physics students. Wang & Owens (1995) stated that PT students performed as well as their traditional counterparts on a combined physics and technology test when the variables for overall GPA and grades in mathematics and science were controlled.
The relative scarcity of comparative data for students enrolled in applied academics versus traditional academics indicates a need for this information, particularly given the recent climate of curricular reform and the level of implementation of applied programs in high schools. In addition, advances in the field of multilevel models offer improved analytical procedures for data of this nature. This causal-comparative study ( Issac & Michael, 1995 ) was designed to acquire, compare, and contrast multilevel data for students enrolled in high school applied academic and traditional academic courses. Two areas were the focus of the data collection activity: (a) student demographics and (b) students' ability to apply traditional physics concepts to work-related problems.
Method
InstrumentThe sample for the study was drawn from a population of high school students, grades 9 through 12, enrolled in Iowa public high schools during the 1995-1996 school year. During the initial stages of the project, each of the 15 Iowa regional tech prep coordinators was asked to recommend four high schools in her or his region perceived to have representative applied academics programs with significant proportions of their student bodies participating in applied academics. At various times during the selection process, meetings were held with these regional coordinators to address questions and ensure that consistent program and course definitions were employed. The schools chosen for the study were selected from this list of approximately 60 Iowa high schools. Representatives from all 60 high schools recommended by the coordinators were phoned regarding the applied academics courses offered. The final cut to six schools was made after looking at several school characteristics, including class size and the willingness of teachers, administrators, and students to participate in the study; and whether the instructional methods were 100% applied, 100% traditional, or some blend of the two methods. Students were included in this study as a result of their pre-existing enrollment in either applied academics courses or equivalent traditional courses. The data were sorted according to applied or traditional course enrollment. The sample included 529 students from 48 intact 3 classes. Of these 529 students, 391 reported Iowa Test of Educational Development 4 (ITED) scores, and 523 had Grade Point Average (GPA) figures available. Only one student was missing both ITED and GPA scores. Students were also asked to self-report the number of units of math, science, and technology they had completed at the time of test administration: 371 reported the number of math units completed, 365 the number of science units, and 343 the number of technology units. Accommodations were made in the analysis on a caseby- case basis for those students providing incomplete data. Individual student data series were eliminated when the analysis included variables for which the student did not supply data. When the analysis was restricted to variables for which the student did supply data, that information was retained, even if the student had missing data with respect to other variables. For example, one could look at the distribution of all 522 students providing GPAs, when GPA was the variable of interest, even if only 384 reported both GPA and Iowa Tests of Educational Development (ITED) scores.
ProcedureThe instrument used to indicate a student's ability to apply traditional physics concepts to work-related problems (the dependent variable) was the Work Keys Applied Technology (AT) test. The test score served as the measure of a student's technology skill level. As described in the Work Keys Preliminary Technical Handbook ( ACT, 1997 ):
The Applied Technology assessment measures the examinee's skill in solving problems of a technological nature. The content covers the basic principles of mechanics, electricity, fluid dynamics, and thermodynamics as they apply to machines and equipment found in the workplace. Because the assessment is oriented toward reasoning rather than mathematics, any calculations required to solve a problem can be readily performed by hand. The emphasis is on identifying relevant aspects of problems, analyzing and ordering those aspects, and applying existing materials or methods to new situations.
This assessment contains questions at four levels of complexity, with Level 3 being the least complex and Level 6 being the most complex. Although Level 3 is the least complex, it still assesses a level of applied technology skill well above no skill at all. The levels build on each other, each incorporating the skills assessed at the preceding levels. Examinees are given 45 minutes to answer 32 multiple-choice questions. (p. 70)
Estimates of reliability parameters for the AT assessment test are included in ACT's Preliminary Technical Handbook ( ACT, 1997 ). The coefficient alpha for the AT assessment is reported as .80 ( ACT, 1997 , p. 36), although a qualifier is added pertaining to the multi-dimensionality of the test. ACT explains that this assessment includes mechanical, electrical, thermodynamic and fluid dynamic topics, which tends to lower the internal consistency of the assessment, but may enhance the validity with respect to job performance ( ACT, 1997 , p. 37).
The approach followed by ACT with respect to content validation was to use panels of qualified content domain experts in the test development process. The development process included input by advisory panels composed of business people and educators knowledgeable in the topic areas, and examination by both content and fairness reviewers. After reviewing the results from 765 profiled jobs, ACT concluded that the results "strongly suggest" that the Work Keys skill scales are content valid for large numbers of jobs ( ACT, 1997 , p. 52). A more in-depth discussion of reliability and validity is included in ACT's Preliminary Technical Handbook ( ACT, 1997 ).
Hierarchical Model AssumptionsA project team worked with each school to identify and schedule specific classes to take the Work Keys assessment tests. This team also worked with individuals knowledgeable about applied academics implementation in Iowa to identify equivalent courses for comparison. The course equivalencies suggested by this group were: Applied Math I and Algebra I; Applied Math II and Algebra II, Trigonometry, or Geometry; Applied Communications and Basic Communications, Composition, or Composition and Literature; Principles of Technology I and Physics; and Applied Biology/Chemistry and Traditional Biology/Chemistry.
The following data were requested from all 529 students in the target classes during the 1995-1996 school year: (a) high school; (b) course type-applied or traditional; (c) course-math, English, physics, etc.; (d) student grade level-9 through 12; (e) student cumulative high school grade point average-0 to 4.00; (f) percentile rank of the student's ITED composite score-0 to 100; (g) number of units of math, science, and technology previously completed; and (h) specific applied and traditional courses previously taken-selected from a list. The AT test was administered to all students near the end of the 1995-1996 school year.
Once these data were collected, both descriptive analyses and exploratory data analyses (EDA) were conducted. These analyses included examination of the univariate distributions and bivariate relationships of variables. Multiple graphical procedures were employed to review the data prior to any hierarchical modeling. Residual analysis was also employed during the hierarchical modeling process. These examinations were needed to provide insight into the tenability of model assumptions, the validity of which can affect the legitimacy of statistics developed from those models.
Design
- The within-class errors for Level-1 predictor variables (such as grade level and gender) are normal and independent with class means of zero and equal variances across classes.
- Whatever student-level predictors of employability skills (Work Keys assessment test results) are excluded from the model and thereby end up in the Level-1 error term, e (ij) , are independent of a student's included Level-1 predictor variables.
- The vector of residual class effects (r 0(j) , r 1(j) , r 2(j) , r 3(j) ) is multivariate normal, with mean vector (0, 0, 0, 0) and its related variance-covariance matrix.
- Whatever class-level predictors of the intercept and student-level coefficients are excluded from the model and thereby end up in the Level-2 error terms, for example r 0(j) , are independent of the included class-level (Level-2) predictor variables, such as curricula type.
- The error at Level-1 is independent of the Level-2 error terms ( Bryk & Raudenbush, 1992 ).
EDA uncovered outliers, which were identified during the residual analysis done as a part of hierarchical model development. These outliers (five classes and ten students) were removed from the data set.
Hierarchical ModelsMultilevel models, based on the Hierarchical Linear Models (HLM) approach discussed by Bryk and Raudenbush (1992) , were used. Data for intact classes at the student, class, and school level were gathered for analysis; however, the decision regarding the unit of analysis for the two groups of students (that is, those enrolled in applied versus traditional classes) was not clear-cut. Traditional linear model analysis assumes linearity, normality, homoscedasticity, and independence ( Bryk & Raudenbush, 1992 , p. xiv). Whether data are normally distributed is easily checked and nonparametric methods exist to accommodate data that do not meet the standard assumption of normality. One would have difficulty, however, making a case for the assumption of independence at the individual student level since groups of students are aggregated in classes; and to perform the analyses solely on aggregated level data ignores the wealth of within-class variation. These unit-of-analysis questions have been the focus of a number of researchers over the past 25 years ( Bryk & Raudenbush, 1992 ; Cronbach & Webb, 1975 ; Iversen, 1991 ; Pedhazur, 1982 ) and multilevel models are increasingly being used to address unit-of-analysis concerns. Although it is beyond the scope of this paper to cover aspects of building and assessing hierarchical models, the fundamental reason for their use is to lessen concerns associated with the choice of a unit-of-analysis. The initial three-level (students within classes within schools) hierarchical model used is described below. The mathematical representation of a two-level model used in this study is provided in the Appendix.
Level-1 : Within each classroom, students' abilities to apply physics principles to technical work-related problems (Work Keys Applied Technology assessment test scores) are modeled as a function of a number of student-level predictors, potentially including gender, grade level, ITED score, GPA, previous course work in math, science, or technology, and a random student-level error.
Level-2 : Each Level-1 coefficient is modeled by classroom-level characteristics such as curricula type (applied or traditional) and relevant topic (physics and PT versus other) for a class.
Level-3 : Each Level-2 coefficient is modeled by an assessment test score grand mean plus a random school-level error term.
Results
Table 1 provides the gender and grade level cross-tabulations for the two student groups, applied versus traditional. The demographics of the groups varied noticeably in two areas: The percent of students in 12 th grade relative to their group, and the ratio of females to males in the samples. Students in the 12 th grade comprised approximately 32% of the applied student total, but 69% of the traditional student total. In terms of female to male ratio, there were over twice as many males as females in the applied group (172:77), while there were slightly more females than males in the traditional group (145:135).
Table 1
Gender and Grade in School
Applied Courses Traditional Courses
Female Male Female Male Totals
9 th 39 35 9 13 96 10 th 5 46 34 17 102 11 th 11 34 10 3 58 12 th 22 57 92 102 273 Totals 77 172 145 135 529
One initial area of interest related to student demographics was the difference between students above and below the minimum skill level cutoff score of three on the AT test. Table 2 presents a detailed cross-tabulation of test results for students enrolled in specific courses. Overall 42% of the students scored below the minimum skill level assessed by the test. Students enrolled in physics had the best performance with only 15% scoring below the minimum skill level. Students in all other courses did not fare as well with 40% to 57% scoring below the minimum skill level.
Table 2
Number of Students by Course Scoring Above and Below Minimum Skill Level Cutoff on the Applied Technology Work Keys Test
Students Completing Applied Technology Test Frequency of Scores
Courses <3 ≥3 Totals <3 as % of Total
Applied Math I 3 3 6 50% Algebra I 0 0 0 0% Applied Math II 2 2 4 50% Algebra II or Geometry 0 0 0 0% Applied Communications 26 23 49 53% Traditional English Courses 29 44 73 40% Principles of Technology I 43 54 97 44% Physics 18 105 123 15% Applied Biology/Chemistry 52 41 93 56% Traditional 48 36 84 57% Biology/Chemistry Totals 221 308 529 42%
Note . Using students enrolled in the traditional physics classes as an example, one can interpret this table as follows: Of the 123 students enrolled in Physics and completing the Applied Technology test, 18 students scored below Level 3 (the minimum skill level required to effectively perform certain profiled jobs) and 105 scored at or above Level 3; therefore 15% did not meet the minimum skill level assessed by the test.
A statistically significant gender gap also emerged with respect to the incidence of males and females falling below the minimum competency score on the test. More males than females (307:222) took the Applied Technology test, however, fewer males than females (100:121) scored below the minimum competency cutoff score of three.
Means (with standard deviations in parentheses) for ITED scores and Grade Point Averages (GPA) for students who scored below the minimum skill level score on the Applied Technology test, and for whom GPA and ITED data were available, were 36.03 (23.55) and 2.48 (0.79) respectively. The n s were 147 and 215 respectively. Clearly, students falling below the minimum skill cutoff score of "3" were not only those with an ITED score or GPA at the low end of the scale.
There are clear differences in the demographics and academic performance of the two groups of students in this investigation. The overall ratio of male to female students taking the Applied Technology test was 307 to 222; however the proportions were different within the applied versus traditional courses. The ratio in the group of students enrolled in applied courses was 172 males to 77 females; for the group of students enrolled in traditional courses, the ratio was 135 males to 145 females. Both ITED and GPA histograms showed traditional physics students with higher means than applied students in comparable Principles of Technology 1 courses (see Figure 1). Students enrolled in physics were almost exclusively in grade 12: Of the 123 students in physics, 121 were in grade 12, one was in grade 10, and one was in grade 11. Students enrolled in Principles of Technology were more evenly distributed through grades 10, 11, and 12 with 29, 37, and 19 students respectively. One student in grade 9 was enrolled in Principles of Technology.
Figure 1 . Histograms comparing Principles of Technology 1 students' GPA and ITED scores with those of students enrolled in traditional physics.
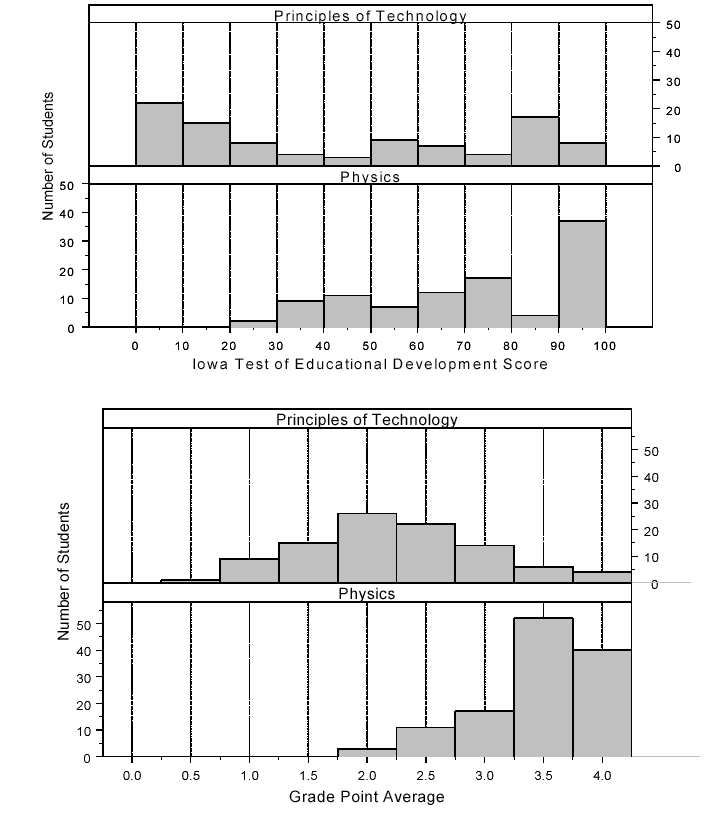
During exploratory data analysis, a significant zero-order correlation ( r = .80 at p = .00) was observed between two variables, ITED scores and GPA, expected to provide information regarding previous academic performance. The fact that the original two variables were highly correlated made it advisable to examine the Variance Inflation Factors (VIF) to determine if one of the variables should be removed from consideration. An Ordinary Least Squares (OLS) Regression of the Applied Technology Work Keys score on GENDER, GRADE, GPA, and ITED variables yielded VIF values between 1.030 and 2.908. Since all four variables yielded VIF values well below 10-the value suggested by Neter, Kutner, Nachtsheim, and Wasserman (1996 , p. 386) as indicative of multicollinearity that may be unduly influencing the least squares estimates-none were rejected out of hand.
Applied Technology HLM AnalysisThe differences in the AT test scores between the two student groups were analyzed using HLM techniques. When evaluating data, the choice of number of levels is primarily data driven. One initially looks at a fully unconditional model where one does not attempt to explain variance but simply partition it among levels. A fully unconditional model is characterized by the absence of predictor variables at all levels. In other words, the AT test score is modeled at all levels as a function of a mean score plus a random error.
The decision is then made based on the fully unconditional model as to whether the amount of variation at a specific level is enough to warrant including that level in subsequent models. During this investigation, 85% of the variance was observed at Level 1 (that is, within class or between student variation), 14% of the variance was associated with Level 2 (between classes), and only 1% was observed at Level 3 (between schools); therefore, a three-level model was rejected in favor of the less complex two-level model with Level 3 variance included in the Level 2 error term.
A variety of predictor variables were evaluated at Level 1 of the model, including ITED and GPA scores, GENDER, and GRADE (the student's year in school). Also considered at Level 1 were variables covering the self-reported number of units previously taken by students in the areas of math, science, or technology; and prior enrollment in applied math, traditional math, or physics courses. Two predictor variables were also evaluated at Level 2 of the model; TYPE (applied versus traditional course) and RELVNT (a dummy variable used to indicate whether or not the course material was relevant to the material covered in the AT test-for example, physics and principles of technology courses were relevant to the AT test, while all other courses were not). No school-level predictor variables were used since the variance decomposition indicated that little of the variability associated with the test scores could be attributed to Level-3, or school-level, variables.
Implications for Technology CurriculaThe output of the HLM analysis, with respect to estimates of coefficients, is similar to what one might find when performing a simple linear regression such as Y = b 0 + b 1 X. Given values for X, the estimates of these coefficients may be used to predict Y-values. The estimated coefficients for significant variables in the final HLM model are provided in Table 3. Table 4 provides estimates of some additional coefficients that did not prove to be statistically significant and were removed in the final model.
Table 3
HLM estimates for Applied Technology data--significant variables only
Fixed Effect Coefficient se t ratio p value
Grand mean, β 00 0.529 0.250 2.111 .047 Relevant course, β 01 0.494 0.173 2.864 .010 Gender, β 10 0.891 0.182 4.895 .000 GPA, β 20 0.365 0.186 1.959 .050 ITED, β 30 0.016 0.005 2.904 .004 Number of Math Units, β 40 0.009 0.002 4.717 .000 Number of Science Units, β 50 0.007 0.001 6.232 .000 Prior Enrollment in Traditional 0.863 0.280 3.086 .002 Math, β 60
Variance Random Effect Component df χ 2 p value
Level 1 e (ij) 2.30555 (Students), Level 2 (Classes), r 0(j) 0.00063 21 15.179 >.500
Variance Reduction (by level) from Unconditional Model
Level 1 Students 20.1% Level 2 Classes 99.9%
Note . Almost all (99.9%) of the class-level variation is explained by the Applied Technology model. Noting that p > .500 for the random effect at Level 2, one may conclude that a minimal amount of unexplained variation remains at this level.
Table 4
Comparison of HLM and OLS Coefficients
HLM 1 OLS 1 HLM 2 OLS 2 Sample Size Classes 40 25 Students 435 369 294 216
Coefficients Relevant .320* .309 .556 .459 Type -.132 -.217 -.057 -.044 Gender 1.016* 1.046* .870* .927* Grade .109 .102 -.053 -.023 ITED .022* .027* .017* .035* GPA .467* .422* .367 .278 Math Units .010* .006 Science Units .008* .006 Prior Traditional .884* .641 Math
* p ≤ .05
The curriculum "Type" coefficient for the AT test as shown in Table 4 is -0.057 for a sample size of 25 classes. The coefficient is not significant for this data set with p = .80, indicating that while students enrolled in traditional courses score slightly lower on average than students enrolled in applied courses when controlling for various academic and demographic factors, that difference was not statistically significant. The significant "Relevant course" coefficient shown in Table 3 is positive, indicating that students enrolled in physics or technology courses did better on the technology test than did students enrolled in English, biology, and chemistry courses. The students enrolled in relevant courses scored on average one-half point higher than those enrolled in non-relevant courses.
Male students scored on average 0.891 points higher on the AT test than did female students. Both GPA and ITED coefficients are positive, which unsurprisingly indicates that those students with higher GPA and ITED marks earned, on average, higher scores on the AT test than did those with lower GPA and ITED marks. What was somewhat surprising, however, was that the grade level of the student-that is, whether a student was in grade 10, 11, or 12-did not yield a statistically significant result. While it might be argued that one or more of the significant variables, such as number of math and science units taken, could be correlated with grade level and thus account for differences in grade level performance, a check of the variance inflation factor for "GRADE" with other significant variables in the regression equation yielded an unremarkable 2.477. Other statistically significant variables included the self-reported number of units of mathematics and science completed by the students. However the values of these variables ran from 0 to 10 units each and, given coefficient values of .009 and .007 for math and science units respectively, the average impact of these prior academic components would be minimal on the overall assessment test score, a combined maximum of .160 points. The remaining statistically significant coefficient indicated that students with prior coursework in traditional mathematics scored on average 0.863 points higher on the Work Keys assessment than those without prior courses in traditional mathematics.
Once again, as was stated earlier, all data were not available for all 529 students. For example, ITED scores and self-reported data regarding number of units of mathematics and science previously taken by students were particularly prone to falling in the missing data category. In order to gain some measure of information regarding how robust the above estimates were to changes in sample size and analytical method, two iterations of both HLM and Ordinary Least Squares (OLS) regression models were employed (see Table 4). Although OLS models were not considered optimum for these data sets, due to concerns about the independence of student-level data within classes, the models did allow comparisons of the signs (positive or negative), magnitudes, and levels of significance of the coefficients relative to the HLM models. The results indicated that the coefficients were relatively stable, and more importantly, the type of instruction, applied versus traditional, was not significant in any of the models.
Conclusions and Discussion
Examination of the demographics and academic performance of the two groups of students in this investigation indicate clear differences. A comparison of AT test scores, without controlling for other variables, suggest a conservative Cohen's d effect size of .42, which falls between what Cohen (1988) would describe as a small effect size, d = .2, and a medium effect size, d = .5. However, once a student's gender and ITED score are taken into account by regressing the AT test scores on these two variables and examining the residuals, Cohen's d effect size drops to .04, suggesting essentially no treatment effect (applied versus traditional instruction). The fact that students enrolled in applied courses exhibit, on average, lower ITED scores and GPAs may indicate that less academically gifted (or motivated) students are steered toward the applied courses, and that applied courses are not viewed as favorably as traditional courses by students in the academic upper quartile. Indeed, this is not a unique perspective. Lakes and Burns (2001) , for example, passed along a harsh assessment offered by an instructor in their study. In the instructor's view, the applied program was a dumping ground for those with learning disabilities within the population of non-college-bound students (p. 33). Dare (2000) also provides a welldocumented discussion of problems associated with applied academics, including the all-to-common failure of four-year institutions to award college credit for applied academics.
In addition, the ratio of male to female students is considerably different within the applied versus traditional courses. Over twice as many male students as female students were enrolled in applied courses, while traditional courses exhibited a more even split. One outcome of the study that perhaps warrants further investigation relates to the high numbers of students (42%) scoring below the minimum competency cutoff score on the AT test. If this test is to be used to evaluate student performance in the future, researchers should be confident that the results are truly the product of a competency gap and not somehow a test validity issue.
A statistically significant gender gap emerged with respect to the incidence of males and females falling below the minimum competency score on the test. More males than females took the AT test, however, fewer males than females scored below the minimum competency cutoff score. These data are in line with results from the National Assessment of Educational Progress reported by Scaife (1998) : "The performance gap in physics between 11 th grade girls and boys was found to be extremely large, and it could not be explained by differential course-taking patterns … " (p. 63).
As regards the grade distribution of students enrolled in traditional physics versus the grade distribution of students enrolled in Principles of Technology 1, the fact that the applied course seems to be drawing students into a technical elective at an earlier age might be considered a benefit of the curriculum.
First, one should not generalize based on this study that the instructional methods yield equivalent results, or that one instructional method is "better" than the other. The use of intact groups and potential problems associated with attempting to statistically control for intact group differences would make such conclusions questionable ( Pedhazur, 1982 ). One could also argue that the benefits of the applied instructional method go far beyond improved performance on tests ( Hull, 1995 ) even if there were statistically significant differences in test results. Disparities do, however, exist in raw Work Keys test performance, mean GPAs, and mean ITED scores between those groups of students enrolled in applied academic courses and those groups of students enrolled in the comparable traditional academic courses. In all cases, the students enrolled in traditional courses had higher average raw scores than did the students enrolled in the comparable applied courses. To a certain extent this might be expected for the Principles of Technology courses versus physics courses, since applied courses are targeted toward the academic middle fifty-percent of high school students ( CORD, n.d. ; Wang & Owens, 1995 ) and physics is typically an elective taken by 12-graders with above-average academic performance. While this disparity might be cause for concern for some, others might be gratified to see students taking the Principles of Technology course who might not otherwise have been enrolled in any type of physics-based course. The applied PT program does appear to be reaching a different audience than the traditional physics course, and pulling them into the topic area at an earlier age. Thus, while there are significant differences between raw academic performance for those enrolled in applied academics courses as compared to students who are enrolled in equivalent traditional courses, performance on the applied technology assessment instrument is comparable for the two groups of students when certain demographic variables such as gender, GPA, and ITED scores are taken into account. Given the importance of technical competency in today's workplace and the number of students that do not appear to meet even the minimum workplace requirements (42% for the combined sample groups), a curriculum that draws in a broader audience and provides exposure to important technical concepts would seem to be a valuable contributor to developing technology competency, one of the five SCANS (1991) competencies needed to "span the chasm between school and workplace" (p. xv).
The study has yielded information that may benefit future investigations into the effectiveness of the applied academic instructional method. Longitudinal studies of each group's performance relative to a number of indices including, but not restricted to, test scores would be a start. Test scores are certainly one measure of student learning under a particular type of instructional method; however, they do not provide the whole picture. Even if average test scores of students enrolled in applied classes never reach levels observed with college-bound traditional students, one could argue that progress is being made toward the technology component of the SCANS competencies ( SCANS, 1991 , p. xvii) by increasing the technology literacy of students who might otherwise have never enrolled in a technology course.
The data in this study indicate the diversity of the two groups under consideration, but further work must be done to generalize the essential question of comparative performance over time. That question requires that one monitor growth of students' technical skills. Data should be collected at periodic intervals for analysis and should include measures of performance in both school and workplace. Tracking changes over time is of particular importance if the measures of effectiveness apart from test scores, such as shifts in technical course enrollment, are to be examined. Care must also be taken in the choice of when data are collected. One data collection site reported that students, particularly seniors, were less apt to put forth their best efforts when tests were administered near the end of the school year ( Dugger et al., 1996 ). Finally, future research should include investigation of other independent variables that may account for the significant unexplained variability related to AT test scores. These types of data are crucial to decisionmakers in their efforts to evaluate the impact of applied academics in today's schools.
Appendix
One form of the two-level (students within classes) hierarchical model used in this investigation is described below. It should be noted that not all variables identified as significant in the final model are included in this example.
Level-1 : Within each classroom, students' abilities to apply traditional physicsbased concepts to work-related problems (Work Keys Applied Technology assessment test scores) are modeled as a function of a number of student-level predictors; for example gender, grade level, ITED scores, and a random student-level error:
Y (ij) = π 0(j) + π 1(j) a 1(ij) + π 2(j) a 2(ij) + π 3(j) a 3(ij) + e (ij)Where
Y (ij) is the Work Keys test score of student i in class j . π 0(j) is the mean Work Keys score of grade 9 females with a grand-mean centered ITED score in class j . π 1(j) is the predicted change to mean Work Keys score in class j when the student is a male. This is a "gender" coefficient. a 1(ij) is a dummy variable associated with student gender. The coding is 0 for a female student and 1 for a male student. π 2(j) is the predicted change to mean Work Keys score in class j as a result of the student's grade level (9, 10, 11, or 12) a 2(ij) is a dummy variable associated with student grade level. The coding is 0 for a student in grade 9, 1 for a student in grade 10, 2 for a student in grade 11, and 3 for a student in grade 12. One might question the representation of grade as an interval variable in this case, as is implied by the coding, but it was considered to be a reasonable tradeoff to maintain a higher number of degrees of freedom in the model. In addition, models were run using three binary dummy variables for grade level. The grade coefficients using three binary dummy variables for grade did not prove to be significant at the .05 level either. π 3(j) is the predicted change to mean Work Keys score in classroom j per unit change in the student's grand-mean centered ITED score. a 3(ij) is the grand-mean centered ITED score of student i in class j . e (ij) is a Level-1 random effect that represents the deviation of student ij 's score from the predicted score. These residual effects are assumed normally distributed with a mean of 0 and a variance of σ 2 . Level-2 : Each Level-1 coefficient is modeled by some classroom-level characteristics such as curricula type (applied or traditional) and relevant topic (technology or non-technology) for a specific class.
π 0(j) = β 00 + β 01 Χ 1(j) + β 02 Χ 2(j) + r 0(j)Where
π 1(j) = β 10
π 2(j) = β 20
π 3(j) = β 30
β 00 is the grand mean Work Keys test score of grade 9 females with grandmean centered ITED score in applied non-technology courses. β 01 is the predicted change to overall class mean Work Keys test scores of grade 9 females with grand-mean centered ITED scores in nontechnology courses from the grand mean Work Keys test score when traditional curricula are used rather than applied curricula. This is a "curricula-gap" coefficient. Χ 1(j) is a variable associated with curriculum type used in classroom j . The coding is 0 for an applied and 1 for a traditional course. β 02 is the predicted change to overall class mean Work Keys test scores of grade 9 females with grand-mean centered ITED scores in nontechnology courses from the grand mean Work Keys test score when the applied course is a technology course rather than a non-technology course. This is a "relevant course" coefficient. Χ 2(j) is a dummy variable used to identify whether or not a course is "relevant" to the Work Keys test taken . The coding is 0 for a non-relevant course and 1 for a relevant course. r 0(j) is a Level-2 random effect that represents the deviation of class j 's Level- 1 intercept coefficient from its predicted value based on the Level-2 model. The random effects in Level 2 equations are assumed multivariate normal with a mean of 0. The variance of this effect is designated as τ π . β 10 is the mean slope, averaged across classes, relating student gender to Work Keys score. When the coefficient is considered a fixed effect, as it is here with π 1(j) assumed equal to β 10 , it implies that there are not statistically significant differences in the relationship between a student's gender and the Work Keys test score from class to class within a school. β 2 is the mean slope, averaged across classes, relating student grade to Work Keys score. β 30 is the mean slope, averaged across classes, relating students' grand-mean centered ITED scores to Work Keys score. References
ACT Center for Education and Work. (1995) . Making the grade: Keys to success on the job in the 90s [Brochure]. Iowa City, IA: Author.
ACT. (1997) . Work keys preliminary technical handbook . Iowa City, IA: Author.
Bennett, C.A. (1926) . History of manual and industrial education up to 1870 . Peoria, IL: Chas. A. Bennett Co., Inc.
Bennett, C.A. (1937) . History of manual and industrial education: 1870-1917 . Peoria, IL: The Manual Arts Press.
Bryk, A.S. & Raudenbush, S.W. (1992) . Hierarchical linear models: Applications and data analysis methods . Newbury Park, CA: SAGE.
CORD. (n.d.) . Principles of technology: A contextual approach to workplace physics [Brochure]. Waco, TX: Author.
Cronbach, L. J., & Webb, N. (1975) . Between-class and within-class effects in a reported aptitude x treatment interaction: Reanalysis of a study by G. L. Anderson. Journal of Educational Psychology , 67(6), 717-724.
Dare, D. E. (2000) . Revisiting applied academics: A review of a decade of selected literature. Journal of Vocational Education Research , 25(3), 296-332.
Dugger, J. & Johnson, D. (1992) . A comparison of principles of technology and high school physics student achievement using a principles of technology achievement test. Journal of Technology Education , 4(1), 19-26.
Dugger, J. C., Lenning, O. T., Field, D. W., & Wright, A. (1996) . Report to the Iowa Department of Education: Statewide pilot study and development of a model for evaluating applied academics across Iowa . Ames, IA: Iowa State University, Department of Industrial Education and Technology.
Dugger, J. & Meier, R. (1994) . A comparison of second-year principles of technology and high school physics student achievement using a principles of technology achievement test. Journal of Technology Education , 5(2), 5-14.
Goldberger, S. & Kazis, R. (1996) . Revitalizing high schools: What the school-tocareer movement can contribute. Phi Delta Kappan , 77(8), 547-554.
Hershey, A., Owens, T., & Silverberg, M. (1995) . The diverse forms of tech-prep: Implementation approaches in ten local consortia . (MRP reference: 8087). Princeton, NJ: Mathematica Policy Research.
Hull, D. (1995) . Who are you calling stupid ? Waco, TX: Center for Occupational Research and Development.
Isaac, S. & Michael, W.B. (1995) . Handbook in research and evaluation: A collection of principles, methods, and strategies useful in the planning, design, and evaluation of studies in education and the behavioral sciences (3rd ed.). San Diego, CA: EdITS
Iversen, G. R. (1991) . Contextual analysis . Newbury Park, CA: SAGE.
Lakes, R. D., & Burns, J. Z. (2001) . "It's like their culture:" Resistant boys in the new vocationalism. Journal of Industrial Teacher Education , 38(4), 25-40.
Neter, J., Kutner, M. H., Nachtsheim, C. J., & Wasserman, W. (1996) . Applied linear statistical models (4th ed.). Chicago: Irwin.
Pedhazur, E.J. (1982) . Multiple regression in behavioral research: Explanation and prediction (2nd ed.). New York: CBS College Publishing.
Scaife, J. (1998) . Science education for all? Towards more equitable science education. In A. Clark & E. Millard (Eds.), Gender in the secondary curriculum: Balancing the books (pp. 60-79). London: Routledge.
Secretary's Commission on Achieving Necessary Skills [SCANS] . (1991). What work requires of schools: A SCANS report for America 2000 . Washington, DC: U.S. Department of Labor.
Wang, C., & Owens, T. (1995) . The Boeing Company applied academics project evaluation: Year four. Evaluation report . Portland, OR: Northwest Regional Educational Laboratory. (ERIC Document Reproduction Service No. 381892)
1 Work Keys Tests are a series of tests designed to assess personal skill levels in important areas of employability skills ( ACT, 1997) . There are currently eight tests: (a) Applied Mathematics, (b) Applied Technology, (c) Listening, (d) Locating Information, (e) Observation, (f) Reading for Information, (g) Teamwork, and (h) Writing. 2 Applied academics courses ( Hull, 1995 ) are those developed by the Center for Occupational Development (CORD) or the Agency for Instructional Technology (AIT). The courses are entitled Principles of Technology, Applied Biology/Chemistry, Applied Mathematics, and Applied Communications. Applied courses target the middle 50% of the typical high school student body, incorporate contextual examples, and help students master essential academic knowledge through practical experience (Parnell, 1992). 3 For purposes of this project, the term "intact class" indicates a situation where students who are already enrolled in existing applied or traditional classes are observed rather than randomly assigned to applied or traditional courses. This results in the research being classified as quasi-experimental. 4 Iowa Test of Educational Development (ITED) is a standardized test designed to assess current performance in reading, language, and mathematics. Individual achievement is determined by comparison of results with average scores derived from large representative samples and is communicated as a percentile rank score. Author Note
This investigation uses secondary data collected during a study supported in part by the Iowa Department of Education. Dr. Jan Sweeney, Dr. Mandi Lively, and Mari Kemis of the Research Institute for Studies in Education at Iowa State University were involved in the initial aspects of that study. Team members, besides the author, who were involved throughout the Iowa Department of Education project included Dr. John Dugger, Dr. Oscar Lenning, and Ms. Andrea Wright. A portion of the data collected during that project formed the basis for the author's doctoral dissertation and this manuscript. Dr. Fred Lorenz also deserves recognition for his counsel during the time statistical techniques were being investigated. Finally, thanks to Dr. Michael Dyrenfurth, Dr. Steven Freeman, and Dr. Mack Shelley for critiquing this manuscript. The efforts of all are gratefully acknowledged. Correspondence concerning this article should be addressed to Dennis W. Field, Iowa State University, 216 Industrial Education II, Ames, Iowa 50011-3130. Field may be reached by phone at (515) 294-6332, by fax at (515) 294-1123, and by e-mail at dwfield@iastate.edu