JVME v21n1: Use of a Markov-Chain Model to Evaluate Employment Policies for a Veterinary School Faculty
| Volume 21, Number 1 | Spring, 1994 |
|---|
Use of a Markov-Chain Model to Evaluate Employment Policies for a Veterinary School Faculty
B.A. Montgomery, J.W. Lloyd and A. Jensen
From the Department of Educational Administration (Montgomery),
Population Medicine Center and Department of Large Animal Clinical Sciences (Lloyd),
and Department of Agricultural Economics (Lloyd, Jensen),
Michigan State University, East Lansing, MI 48824.
Introduction
Recent studies have indicated that the number of faculty members will dramatically decrease nationally in the 1990s and that it will be increasingly difficult to replace them. These shortages are related to an increasing number of faculty who are expected to leave higher education through resignation or retirement and a decreasing number of candidates overall. The problem will be particularly serious in high-demand academic fields.
As faculty shortages become a problem, monitoring faculty flow becomes increasingly important. Affirmative action goals will continue to increase in importance which makes analysis of the effects of hiring decisions on the faculty pool even more critical. Coupled with these issues are the economic ramifications of policy changes, since salary costs dominate the expense side of the university budget (1) .
The purpose of this study was to design a planning model useful for projecting college-level faculty dynamics under alternative administrative policies. Of primary interest was the ability to estimate the impact of alternative faculty hiring, promotion, and separation scenarios on future faculty age class structures, tenure ratios, and appointment distributions at the college level. Ultimately, such information could be valuable for predicting budgetary salary requirements. The technique was applied to four separate colleges at Michigan State University, but this report will focus on the College of Veterinary Medicine. It is hoped that it will have broader implications to other U.S. veterinary schools.
Review of Problem and Literature
The central aspect of faculty planning problems lies in what has been termed by Carrter (2) as replacement demand and enrollment demand. Replacement demand includes those factors related to net migration into and out of academic careers. Enrollment demand pertains to the impact of college enrollments on faculty labor markets.
The problem of replacement demand has arisen because of several factors. As described by Bowen and Schuster (3, 4) , the deteriorating conditions on campuses are also making it difficult to attract and retain faculty due to: 1) real and perceived decline in compensation; 2) disproportionately high salaries for new faculty in high-demand academic disciplines creating conditions of salary compression; 3) deteriorating work conditions and generally low morale as a result of tight budgets and shifting institutional priorities and reward systems; and 4) pressure on the junior faculty to publish, on mid-careerists to keep up, and on senior faculty to adjust to the surge toward research.
Faculty planning models were first developed in the 1970s when shifts in enrollment patterns toward professional oriented curricula resulted in a surplus of faculty in some areas and shortages in others (5) . Hopkins defined a faculty flow model as a "planning tool used by decision makers to investigate the various institutional practices that can, and do influence the number of faculty positions to be filled." (6) It is an attempt to mathematically describe relationships between variables used in planning.
Bowen and Schuster (3, 7) estimate that the average annual turnover rate of faculty will increase from 4% in recent years to 6 or 8% in the future largely through early retirement and transfer to other industries and professions outside academe. They find that an increasing number of the most capable college students are opting for employment outside of academe. In 1985, 43% of all PhDs were working outside of higher education. Of the students who graduated with PhDs in 1987, 50% were employed outside of academe, with rates of 70% for PhDs in engineering and 50% for PhDs in the physical sciences (8) .
The faculty planning models eventually evolved into the time-dependent Markov-chain model. Markov-chain models have been used in veterinary medicine to evaluate the epidemiology and economics of several diseases, including foot-and-mouth disease (9) , mastitis (10) , and brucellosis (11) . The basis of this Markov-chain model is a matrix where each row and column corresponds to a current faculty state (e.g., tenure status and age, retirement, resignation or death). The coefficients in the matrix refer to the probabilities with which faculty members move to different states. Transition probabilities can be adjusted from year to year as university policies or external conditions change (12) . The number of members per state must be large enough to avoid violating a primary assumption of Markov-chain models, i.e., the transition probabilities for a state remain constant over time. As a time-dependent model, faculty movements can be projected from year to year. This provides not only a forecast of faculty distributions but a means for adjusting the transition probabilities to reflect changing institutional conditions, policies, or practices.
Table 1. States of the Markov model for faculty planning, CVM, Michigan State University.
State Description 1 Tenure track, assistant professor, age 26 to 35 2 Tenure track, assistant professor, age 36 to 45 3 Tenure track, assistant professor, age 46 to 55 4 Tenure, associate professor, age 26 to 35 5 Tenure, professor, age 26 to 35 6 Tenure, associate professor, age 36 to 45 7 Tenure, professor, age 36 to 45 8 Tenure, associate professor, age 46 to 55 9 Tenure, professor, age 46 to 55 10 Tenure, associate professor, age 56 to 65 11 Tenure, professor, age 56 to 65 12 Tenure, associate professor, age 66 to 75 13 Tenure, professor, age 66 to 75 14 Resignation 15 Termination 16 Death 17 Retirement
Methods
Data for faculty in the Colleges of Veterinary Medicine (CVM), Engineering, Natural Science, and Business at Michigan State University (MSU) were collected from Academic Personnel Records through the office of the provost. The data set included year of birth, contractual year of employment, racial/ethnic background, gender, term year (the year that a faculty member separated from the university), term code (the reason for separation from the university), current academic rank, original appointment status (with or without tenure at the time of appointment), current tenure status, year entered the tenure system, year that tenure was granted, year of promotion to assistant professor and/or associate professor, and annual salary in 1981 and 1991.
The data set included every tenure-track and tenured faculty member in each college between the years 1981 and 1991. As such, the sample in this study was the entire population of faculty in these colleges. Some faculty remained in their college during the time period of interest, others left for various reasons, and others were hired. Thus, the population in 1991 would include some members who were on the faculty in 1981, but not all, and would include some members who were hired after 1981.
The model was designed after Hopkins and Massy (1) and Bleau (13) and provided projections of tenure, academic rank and corresponding appointment rates over time, by age. The model states are reported in Table 1. Transition probabilities were averaged over the study's ten years, resulting in a 17x17 matrix.
Like the Hopkins and Massy (1) and Bleau (13) studies, the MSU transition fractions were obtained from actual movements of each faculty member who served in the colleges of interest. A standardized array table was set up to track each faculty member as he or she moved within his/her college.
The model was initialized with actual 1981 faculty distributions, and projections were accomplished by microcomputer implementation of the model using Microsoft Excel (14) software. Differences between the actual and projected numbers of faculty by state were tested for statistical significance by comparing projected 1991 faculty levels with observed 1991 faculty levels using chi-square goodness-of-fit tests. The transition matrix for each of the four colleges was also used to project faculty distributions in the other three colleges, and differences were tested for significance.
Once the model was developed and initial testing was complete, three alternative administrative scenarios were defined, 1991 data were used for initial faculty distributions, and projections were made to the year 2001. The scenarios included: 1) continuation of historical patterns for new hires, promotion, tenure, and separation; 2) continuation of historical patterns for promotion, tenure, and separation, but allowing no new hires from 1991 to 1996 (as might occur under severe budgetary restrictions); and 3) continuation of historical patterns for new hires, promotion, and tenure, but decreasing the retirement rate by 10% (as might occur with relaxed legal retirement guidelines).
Results
Faculty age and rank distributions for the College of Veterinary Medicine (CVM) are presented in Figure 1. The trend suggested by this figure toward an older, more senior faculty was statistically significant (p = 0.01). Comparable findings were obtained for the other three MSU colleges evaluated.
Figure 1. Observed 1981 and 1991 faculty age and rank distributions, CVM, Michigan State University.
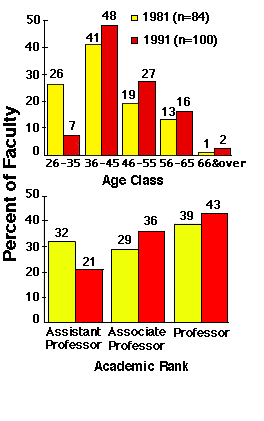
The transition probability matrix obtained for the CVM is presented in Table 2. States 5 (Tenure, professor, age 26-35) and 12 (Tenure, associate professor, age 66-75) were found to be empty during all the years of the study. Also, no CVM faculty were terminated during this time period (state 15).
Table 2. Transition probability matrix of the Markov model for faculty planning, CVM, MSU.1 2 3 4 6 7 8 9 10 11 13 14 16 17 1 0.64 0.17 0.08 0.07 0.04 2 0.82 0.14 0.04 3 0.83 0.18 4 0.50 0.39 0.04 0.06 0.02 6 0.85 0.08 0.02 0.01 0.04 7 0.81 0.17 0.02 8 0.92 0.02 0.03 0.03 0.02 9 0.89 0.08 0.02 0.01 10 0.93 0.01 0.01 0.05 11 0.91 0.03 0.01 0.05 13 0.75 0.05 0.20 14 1.00 16 1.00 17 1.00
Chi-square analysis of observed vs. predicted faculty age and rank distributions for 1991 showed no difference (p > 0.99). Again, similar results were obtained for the other three MSU colleges evaluated. However, CVM projections made with any non-CVM transition probability matrix resulted in predicted faculty rank and age distributions significantly different from those observed (p is less than 0.01).
Figure 2. Observed (1981, 1991) and projected (2001) faculty age and rank distributions, CVM, MSU. Scenario #1.
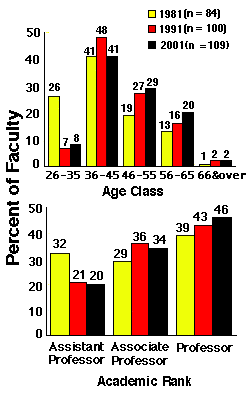
Figure 3. Observed (1981, 1991) and projected (2001) faculty age and rank distributions, CVM, MSU. Scenario #2.
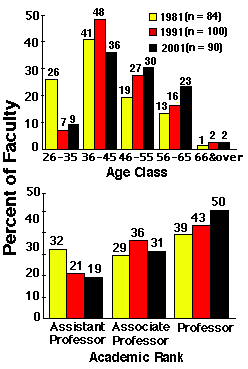
Figure 2 demonstrates the predicted CVM faculty age and rank distributions for the year 2001 if historical patterns for new hires, promotion, tenure, and separation are continued (Scenario 1). Figure 3 presents predictions of the same distributions under a similar assumption for promotion, tenure, and separation patterns, but allowing no new hires from 1991 to 1996 (Scenario 2). Figure 4 shows the model's predictions for CVM faculty if historical patterns for new hires, promotion, and tenure are continued, but the retirement rate is decreased by 10% (Scenario 3).
Figure 4. Observed (1981, 1991) and projected (2001) faculty age and rank distributions, CVM, MSU. Scenario #3.
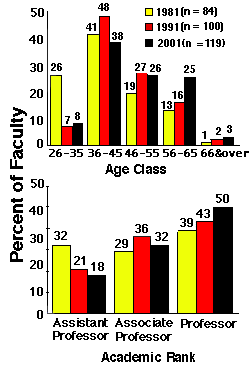
Predictions for each of these scenarios indicate continuation of the trend seen between 1981 and 1991 toward an older, more senior faculty. In general, these results were the same for the other colleges analyzed, though some inter-college differences occurred in the rate of the trend. Though these distributions were not significantly different (p is greater than or equal to 0.75), it is worth noting that the total size of the projected 2001 faculty differs substantially between scenarios (range, n = 90 to n = 119).
Discussion
Based on the results of internal validation, the Markov-chain model developed in this study is an appropriate evaluation tool. It is interesting to note the model's apparent individual- college specificity. From this, it is evident that college-level planning requires college-level modeling.
Total projected faculty size is a critical variable to consider for fiscal planning. This exercise demonstrates that if new hires are temporarily restricted, total faculty numbers can be substantially reduced. At the same time, the results indicate that retirement policy can also have an important impact on salary requirements. As such, successful planning exercises must accurately anticipate policy changes and their accompanying impacts.
The continuing shift toward an older, more senior faculty also has definite implications for budgetary salary requirements. Though the three scenarios evaluated in this study are admittedly cursory for the purpose of preliminary model evaluation, the pattern of results should reinforce similar signals that administrators may be receiving from other sources.
Beyond budgetary requirements, the ideal mix of assistant professors vs. full professors warrants consideration. To maintain optimal productivity, a faculty must be both innovative and stable. Obtaining this target blend is the perpetual challenge of the tenure system, and could logically be facilitated using models such as developed in this study.
Gender/ethnic distributions could be incorporated into this planning model. Though these were evaluated at MSU, they were not modeled in the current study. As diversity in society increases, diversity in the veterinary profession must also increase. As such, vigilance is critical, and future faculty planning models should incorporate diversity issues.
Summary
A Markov-chain model was developed to project faculty dynamics and basic demographics at the college level for Michigan State University, and was implemented via microcomputer spreadsheet. Transition probability matrices were developed using college-specific data from four colleges, including the College of Veterinary Medicine, over the period 1981-1991. Internal validity was assessed by initializing the model with 1981 data, projecting 1991 states, and testing via goodness-of-fit. From 1991, three alternative projections were made to 2001: 1) continue historic promotion patterns, new hire rates and distribution, and separation rates; 2) continue historic promotion patterns and separation rates, but discontinue new hires between 1992 and 1996; and 3) continue historic promotion patterns and new hire rates and distribution, but lower retirement rates by ten percent. It was found that a model developed for use in one college was not adequate for projecting faculty flow in another college. Projected 2001 faculty numbers differed substantially between alternative scenarios, which is useful information for fiscal planning. Predictions for each of the scenarios indicated continuation of the trend seen between 1981 and 1991 toward an older, more senior faculty. This continuing shift has definite implications for both budgetary salary requirements and faculty productivity. In general, this study indicates that quantitative models have much potential to provide useful guidance for faculty planning exercises. Interdisciplinary collaborations can be fruitful in this regard.
References and Endnotes
1. Hopkins DSP, Massy, WF: Planning Models for Colleges and Universities . Stanford, CA: Stanford Univ Press, 1981.
2. Carrter A: Ph.D.s and the Academic Labor Market . New York: McGraw Hill, 1976.
3. Bowen HR, Schuster JH: American Professors: A National Resource Imperiled . New York and Oxford: Oxford Univ Press, 1986.
4. Schuster JH, Bowen HR: The faculty at risk . Change 17(4):13-21, 1985.
5. Bleau BL: Faulty planning models: a review of the literature. Jour of Higher Educ 53(2):195-206, 1982.
6. Hopkins DSP: Analysis of faculty appointment, promotion, and retirement policies. Higher Educ 3:397-418, 1974.
7. Bowen HR, Schuster J: Outlook for the academic profession. Academe 71(5):9-15, 1985.
8. Assn of Am Univs: The Ph.D. Shortage: The Federal Role. Washington, DC: Assn of Amers Univs, Jan 11, 1990.
9. Berentsen PBM, Dijkhuizen AA, Oskam AJ: A dynamic model for cost-benefit analyses of foot-and-mouth disease control strategies. Prev Vet Med 12(3-4):229-243, 1992.
10. Carpenter TE: Microcomputer programs for Markov and modified Markov chain disease models. Prev Vet Med 5(3):169-179, 1988.
11. Beck AC, Dillon JL: Brucellosis eradication planning: an application of simulation modeling. Ag Sys 5:165-180, 1980.
12. Bloomfield S: Comprehensive faculty flow analysis. Applying analytic methods to planning and management. In Hopkins DS, Schroeder RG (Eds): New Directions for Institutional Research 13 . San Francisco: Jossey-Bass, 1977.
13. Bleau BL: The academic flow model: a Markov-chain model for faculty planning model. Decision Sciences 12(2):294-309, 1981.
14. Microsoft Excel, Microsoft Corporation, One Microsoft Way, Redmond, WA 98052-6399.