SPT v11n1 - Reasoning with Safety Factor Rules

Reasoning with Safety Factor Rules

Jonas Clausen and John Cantwell
Division of Philosophy
Royal Institute of Technology
Stockholm,Sweden

Abstract

Safety factor rules are used for drawing putatively reasonable conclusions from incomplete datasets. The paper attempts to provide answers to four questions: “How are safety factors used?”, “When are safety factors used?”, “Why are safety used?” and “How do safety factor rules relate to decision theory?”. The authors conclude that safety factor rules should be regarded as decision methods rather than as criteria of rightness and that they can be used in both practical and theoretical reasoning. Simplicity of application and inability or unwillingness to defer judgment appear to be important factors in explaining why the rules are used.

Keywords: Safety factor, uncertainty factor, decision theory, reasoning, heuristics

Introduction

I’m driving along in my car, and it’s a beautiful day. In front of me on the highway is another car, and as I’m driving rather fast I’m closing quickly. Then I remember the “Three Second Rule”. The rule says that, when driving on the highway, I ought to stay at least 3 seconds behind the car in front for reasons of safety. I slow down and start counting the time between us, and after a few moments I have adjusted the speed and distance so that I’m just over 3 seconds behind the car in front. I relax, as I am now confident that I am driving in a sensible and reasonably safe manner in line with good driving practice.

The “Three Second Rule” is an example of a decision rule, or a decision heuristic , that contains a safety factor, in this case: three seconds. The use of safety factors is widespread. In civil engineering time-tested multipliers from certain key load values ( e.g. estimates of average or maximal load) to reasonable design strengths serve as heuristics for safe construction. In toxicology there are simple heuristics for drawing reasonable conclusions from incomplete datasets regarding chemical effects on humans. These rules make use of uncertainty factors or safety factors as divisors from, say, results obtained in mice to putatively reasonable estimates in humans.

In decision theory rules of thumb have traditionally been regarded with mild suspicion: they have been treated as objects not quite worthy of serious theorizing. Good decision-making should be based on numerical probabilities and utilities, or at least be reducible to these concepts. In the last decade or so, with the advent of computer assisted, and automatic, decision making, this picture has changed. Resource bounded rationality has become a field of its own, and rules of thumb form an important sub-class of decision methods.

In this context decision making with safety factors is a curious hybrid. On the one hand we have the “Three Second Rule” in traffic, an unsophisticated but helpful guide to action. On the other hand we have the systematic application of safety factors in various fields of engineering and in fields like toxicology. In these areas the safety factors involved have been put under close scrutiny, both as regards the proper calibration of the numbers employed in the safety factor and as regards their theoretical status.

In this paper the status of safety factor rules as a decision making tool will be scrutinized. How are they used? Why? When? And what is their place in decision theory? The structure of the paper is as follows. In Section 2 two uses of safety factor rules are presented in more detail (still, rather schematically). One example is taken from toxicology, the other from the design of structural components. In Section 3 we try to place safety factor rules within a larger context of decision theory, somewhat hesitantly identifying safety factor reasoning with a form of ‘satisficing’. Section 4 addresses the question whether safety factor rules should be seen a part of the process that risk researchers call ‘risk assessment’ or if it should be seen as part of the process of ‘risk management’. It turns out that the answer varies and that the use of safety factor rules often makes the distinction difficult to uphold. In Section 5 we discuss the question of safety factor rule justification and the trade-off made in science policy decisions. Conclusions are then presented in Section 6.

Examples of safety factor rules

Partial safety factor method for structural design

A frequently used method for designing structures is the partial coefficient method or partial safety factor method . This can be formulated in several different ways of which the following is one. Assume that the failure propensity of the structure is governed by load type variables S _i and resistance type variables R _j . The safe set of the structure is then assumed given by

g ( S _i , R _j ) ≥ 0

Partial safety factors γ _Si and γ _Rj are numbers equal or larger than unity. The safety margins are considered adequate provided that

g ( S _i γ _Si , R _j /γ _Rj ) ≥ 0

The arguments of the g -function are termed design variables. The variables S _i and R _j are most often chosen as characteristic values, S _ik and R _jk A characteristic values is normally a quantile, such as 0.05 for resistance type variables or 0.95 for load type variables, of the stochastic distribution connected to the variable in question.. The use of characteristic values is recognized as being a vast simplification ( Ditlevsen and Madsen, 2004 , p. 22), since it amounts to representing a stochastic variable by one or a few values.

Although actual regulations are in general more complicated it will suffice for our purposes to look at a one-dimensional variant of the safety factor rules used.

Simplified Partial Safety Factor Rule: S _i γ _Si ≤ R _j /γ _Rj

Subfactors that can enter into γ _S and γ _R are factors representing measurement or model uncertainty and so-called safety classes , meaning to what extent humans will be in or around the structure. (cf. Boverket, 2003 )

An uncertainty (safety) factor rule for human health risk assessment

In toxicology, uncertainty factors are used when making inferences from animal data about dose/response to a reference dose (RfD) ¹ . An RfD is commonly understood as “intended to identify a dose or exposure unlikely to put humans at appreciable risk” ( Brand et al., 1999 , p. 295). Starting off with a key dose value such as an animal bioassay NOAEL (no observed adverse effect level) or BMD (benchmark dose) for a certain effect (often called endpoint ), one then divides it by the safety factor U and the result is the RfD. This is a common rendering of an uncertainty factor definition :

RfD =

NOAEL U A × U H × U S × U D × M

( Gaylor and Kodell, 2000 )

The different divisors are explained as follows:

• U _A is the interspecies factor for using animal data for human response, say from studies on mice. A common value is 10 ( Dourson et al., 1996 ).
• U _H is the intraspecies factor for considering sensitive subgroups in the general human population, such as pregnant women or people with inherited susceptibility to certain substances. Again, a common value is 10, though the factor is at times as low as 1 ( Dourson et al., 1996 ).
• U _S is the chronicity factor for using subacute (very short-time) or subchronic (short-time) data for chronic (long-time) effects. Subacute studies are normally conducted over 14 days, subchronic studies over 90 days and chronic studies over approximately 2 years ( Kalberlah et al., 2002 ). Values less than 10 are normally used ( Dourson et al., 1996 )
• U _D is the database factor for using incomplete data sets, such as studies that do not cover enough of the possible adverse effects. Values for U _D vary from 1 to 100 ( Dourson et al., 1996 ).
• M is the modifying factor to be used for further considerations according to expert judgment and is normally less than 10 ( Dourson et al., 1996 ).

Also, Burin and Saunders (1999) note the following:

The uncertainty factors usually range from 1 to 10 depending on the extent of the uncertainty. As uncertainty is reduced, a smaller factor may be used. (p. 210)

Although the former certainly seems true, the latter is not always the case. Even if a factor of 10 is often the default choice when uncertainty is very large, it is a clear possibility that less uncertainty regarding, say, the relation between sensitivity of rats and humans could warrant a larger interspecies factor than 10 if the information obtained indicated that the substance had effects to which humans were much more sensitive than rats.

An interesting thing about this uncertainty factor definition is that the right side of the equation is available to a risk assessor through a fairly well defined procedure. The NOAEL can be obtained through routine testing and the division of that result by the factors is a simple mathematical procedure. One might then say that the relationship operationalizes the RfD.

The safety factor rule based on the above definition and the common understanding of the RfD is, we would argue, something along the following lines:

NOAEL Rule: A dose less than NOAEL/U is unlikely to put humans at appreciable risk

The NOAEL could of course be exchanged for a BMD for an analogous BMD Rule.

Although something like this can be hard to find stated explicitly, it is hard not to interpret the terms in this way. In fact, the NOAEL Rule we have suggested is an implication of the safety factor definition (NOAEL divided by U gives RfD), the definition of the RfD (being a dose that is relatively “safe”) and a monotonicity assumption ; ² that a smaller dose will always mean less or equal probability of a certain response than a larger dose, and will thus be safer.

Decision theory and safety factor rules

When driving we want to avoid accidents, when building we want to avoid that the structures collapse, the overriding goal of toxicology is to establish at what dosage a substances poses a health-threat to humans. We use safety factors to be on the ‘safe’ side. A number of questions arise.

Why take a perhaps costly measure to be on the safe side? Why not simply follow the course of action that strikes an optimal balance between the values involved (travel time, building cost, risks to human health, etc.)? Classical decision theory tells us to do just this. It claims that an action is rational if it has the highest expectation value of all alternative courses of action, where the expectation value can be expressed by (the o _i :s are the possible outcomes of A, Pr _A (o _i ) is the probability that A will have the outcome o _i , and V(o _i ) is the value of the outcome) :

EV(A) = ☐ Pr _A (o _i ) ☐ V(o _i )

A major problem is that typically we have only a vague appreciation of the probabilities involved in a decision problem, and that a good, non-arbitrary, numerical estimate of the values involved is hard to come by. A second standard criticism is that as a psychological fact we seldom if ever compute probabilities and values in the way prescribed by the expectation value approach, and the very act of computing them would, in some situations, be harmful as it would distract our attention from the situation at hand.

So, finding an optimal balance requires that the different values involved are fully comparable, that the probabilities of adverse outcomes are known (even though they be costly or unethical to acquire), and that we have the time, attention, and money to engage in the activity of optimizing. The three second rule is easy to apply and lets me keep my attention on my driving. We just cannot establish the dose-response curve for a chemical by testing it on humans because of ethical constraints on research. Built structures have so many interrelated components and can be subjected to so many different and varied kinds of external forces that only highly sophisticated computer models can even begin to take in the complexities. These are reasons why the principle of maximizing expected utility is of limited practical use in many areas, but a nagging question remains: are safety factors a good replacement for optimizing?

We must keep in mind what we mean by a ‘replacement’. The principle of maximizing expected value (MEV) or maximizing expected utility (MEU) can be viewed in two ways. On the one hand it can be seen as giving a decision method, an algorithm by which one deduces which action to perform. However, many decision theorists and philosophers that endorse the principle, view it not primarily as a decision method , but as giving a criterion of rightness . A rational person should act so as to maximize expected utility. This is not the same as saying that a rational person should calculate the expected utility before acting, indeed in many cases sitting down to perform a number of calculations would be the wrong thing to do. Rather you should act as if you had done the necessary calculations.

Isaac Levi (1981) has developed a decision theory that, even as a criterion of rightness, relaxes the constraint imposed by classical decision theory. Instead of basing a decision on a single probability function and a single utility function, Levi’s theory allows the rational agent to have sets of probability functions and sets of utility functions, and rational decisions are characterized in terms of these sets.

Levi’s decision criteria are lexicographic . First select those actions that maximize expected utility according to some combination of probability function (taken from the set of probability functions) and utility function (taken from the set of utility functions). If several actions satisfy this constraint, select that action that maximizes the minimal expected utility (the minimal value we get from some probability function and some utility function).

Satisficing

The idea of satisficing was first introduced by Simon as an alternative to classical decision theory. It can be interpreted both as criterion of rightness and decision method , and it can be applied in two different decision phases: choice and pre-choice deliberation. ³ For the choice phase the idea of satisficing can be formulated:

Alternative satisficing (Decision rule interpretation): An alternative is rational iff it has (expected) value that equals or exceeds the aspiration level α .

This is one interpretation of the discussion of procedural rationality in Simon (1976) . The aspiration level α here tells us when an (expected) outcome is “good enough” or “satisfactory”.

The idea of alternative satisficing as a criterion of rightness has been severely criticized. How can it be rational to perform an action that is “good enough” if one knows that there is an alternative that has a better outcome? It has been convincingly argued by Richardson (2004) that this idea is incoherent. In brief, the argument goes that either the concept of value needed for alternative satisficing to work cannot be made sense of or satisficing is uninteresting as a concept. One alternative is that value is of the “all things considered” kind, and then doing something that one recognizes as worse “all things considered” than some other available option, something allowed by alternative satisficing, is simply not intelligible as rational behavior. If value is not of this kind, then “satisficing will merge indiscriminately with the simple and banal idea of tradeoffs.” (ibid., p. 108).

Alternative satisficing as a decision method can also be criticized on the same grounds as MEU; that it is, in certain cases, equally impossible for a non-ideal agent to find a satisficing alternative as it is to find an alternative that maximizes expected utility (given extraneous utilities). For example, the agent must in the worst case (only one satisficing option and it is found last, if at all) examine all possible options and compare with the aspiration level, and this task might indeed be intractable.

Taken together, these lines of criticism present a serious challenge to alternative satisficing both as decision method and criterion of rightness.

Deliberation satisficing tells us when to stop our pre-choice search for alternatives and proceed to actually choosing an alternative. This is the “stop rule” or search rule interpretation and can be stated:

Deliberation satisficing (stop rule interpretation): The search for further alternatives can stop iff (at least) one alternative with (expected) value at or above α has been found.

This is an interpretation of the discussion of stop rules in Simon (1972) . Deliberation satisficing understood as a decision method for the “pre-choice choice” or meta choice to search or not, allows it to be made without evaluating search branches. Only currently available alternatives need to be evaluated when deciding whether to look for more. This is of course a potentially huge computational saving, but how well it works depends on how close the aspiration level is to the actual optimum (if there is indeed a well-defined optimum), and it will have the same worst-case characteristics as alternative satisficing. It should be noted that deliberation satisficing says nothing whatsoever about the search process itself, only about when it should begin and end.

Deliberation satisficing can also be seen as a criterion of rightness, and tells us when it is rational to keep on or cease searching, and this is a question that is answered with reference to the values of available alternatives. Again, the question arises of why we should stop the search at some suboptimal point if we know there are better ones (in the sense of all-inclusive value), and the same criticism that was voiced against alternative satisficing as a criterion of rightness can be directed against deliberation satisficing.

An important variation of the stop rule is to relativize it to a particular parameter. For instance, once we find that a particular drug is “safe enough” we can stop looking for safer alternatives, and instead direct our attention to making the production of the drug cheaper. On this interpretation the aspiration level is set not on the combined result (the amalgamation of the different parameters), but on different parameters. This ‘parameterized’ stop rule is of particular interest in settings where diverse values that are difficult to compare are at stake (such as health vs. cost), or where we have good reason to believe that we know some upper limit or approximate optimum in some dimensions but not in others.

Safety factor rules, maximization and satisficing

Consider again the three second rule. It is based on a single, easily obtainable parameter: how many seconds ahead the next car lies. It encapsulates two opposing values: the value of getting to your destination quickly and the negative value of running into the car ahead. It also encapsulates a certain amount of probabilistic information: with a three second safety margin, chances are that if the car ahead slows down quickly, or stops, you will be able to stop without running into it. Part of this probabilistic information is based on knowledge of reaction times, and of the functionality of typical brakes. Thus, for all its simplicity the three second rule encapsulates both the values we ascribe to quick and safe transportation, and considerable knowledge about the behavior of humans and cars.

How have all these different features been combined so as to result in the three second rule, rather than in the four second rule, the two second rule or the 2.9999 second rule? Obviously, the 2.9999 second rule would be dismissed on the basis of being difficult to use. What about the two second rule? Here one can probably argue, and show, that it gives too little margin for people’s widely varying reaction times. The four second rule, on the other hand, could be rejected on the basis that the three second rule provides enough safety anyhow: it is satisficing with respect to safety.

So the three second rule is not taken out of a hat. It can (possibly) be reconstructed as being based on a reasoned weighing of values against probabilities. But, of course, it is still far from being derived using the principle of maximizing expected utility, either in its classical form or in the relaxed version given by Levi. If anything, the three second rule has been derived from practice. One could hope, perhaps in this case even suspect, that with careful numerical estimates of the values and probabilities involved, we could derive the three second rule, but, in this case at least, such an analysis seems pointless: the rule works well enough.

In much of this the three second rule has features similar to those of safety factor rules used in engineering and toxicology. In these areas too, the safety factors encapsulate both values at stake and specific knowledge about the processes involved. In these areas too, the safety factor chosen is taken to give a ‘big enough’ safety margin (satisficing with respect to safety) and endeavor to smooth out individual differences in specific materials and humans. One would suspect, however, that in these areas we would not accept the cavalier attitude that the safety factors are not in need of further analysis on the grounds that they ‘work’, for our impression that they work can be based on scarce information. And indeed it is part of the praxis of these disciplines to refine the grounds from which safety factors are derived. But lack of information will always be a problem and to some extent the safety factors have been chosen because they ‘work’.

To conclude this section, superficially, safety factor rules appear quite far away from the paradigm of using MEU (or Levi’s variation) as a decision method. However a closer analysis shows that they encapsulate both probabilistic and value-based information, but encode a satisficing element with regards to safety.

Practical and theoretical reasoning in risk assessment and risk management

The standard model of the relation between risk assessment and risk management is sometimes simply called the risk assessment/management paradigm . The model is temporally ordered in the sense that research must be concluded (insofar as research can be concluded) before assessment can conclude, and assessment concluded before management. However, initiation of e.g. the management subprocess will at times be first in the chain of events, so the order of initiation is not as clear. Questions for which there are no readily available answers are passed to the left in the model and answers returned to the right (see Fig I).

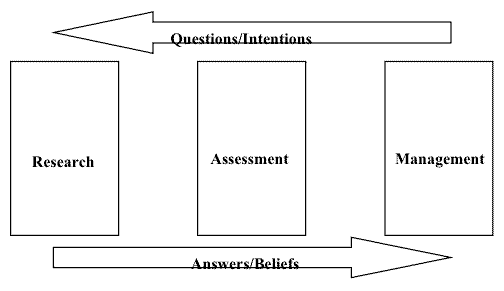
Figure    Flow of intentions and beliefs in the risk

assessment/management paradigm.

Although research, assessment and management each can happen more or less independently, the leftmost subprocesses can be “nested” in a process to the right – research can be nested in the assessment process and assessment nested in the management process. The nesting is, to put it simply, the result of questions flowing left in the model and answers flowing right.

“Science and Judgment in Risk Assessment” ( National Research Council, 1996 ) describes risk assessment of chemicals as follows:

Human-health risk assessment entails the evaluation of information on the hazardous properties of environmental agents and on the extent of human exposure to those agents. The product of the evaluation is a statement regarding the probability that populations so exposed will be harmed, and to what degree. The probability may be expressed quantitatively or in relatively qualitative ways. (pp. 25-26)

While risk assessment is often thought of as science-based, risk management involves further considerations. Just as with risk assessment, “Science and Judgment in Risk Assessment” contains a description of risk management of chemicals:

Risk management is the term used to describe the process by which risk assessment results are integrated with other information to make decisions about the need for, method of, and extent of risk reduction. Policy considerations derived largely from statutory requirements dictate the extent to which other factors – such as technical feasibility, cost and offsetting benefits – play a role. (p.28)

Gaylor and Kodell (2002) distinguish between safety factors that are risk reduction factors and those that are just estimations of quotas between the dose-response curves for different populations (animals/humans or human population in general/sensitive subpopulations). This can Research Assessment Management Questions/Intentions Answers/Beliefs Figure Flow of intentions and beliefs in the risk assessment/management paradigm. be interpreted as a distinction between risk management factors and risk assessment factors. The nature of this distinction will be the topic of part 4.3.

The distinction between risk management and risk assessment superficially parallels the distinction between practical reasoning and theoretical reasoning . Both practical and theoretical reasoning are distinguished by their end results. A piece of practical reasoning is a reasoning process that ends in action or, more plausibly, intention. ⁴ Theoretical reasoning on the other hand ends in belief. There is also what John Broome (2002) calls normative reasoning , which amounts to theoretical reasoning about normative propositions.

In spite of the similarities in end results, with both risk assessment and theoretical reasoning leading to beliefs and practical reasoning and risk management leading to intentions to act, it is not the case that risk assessment is theoretical reasoning, nor that risk management is practical reasoning. The reason for this is that neither risk assessment nor risk management consists only of reasoning. Further, there are practical and theoretical reasoning processes involved in both risk assessment and risk management.

The normativity of safety factor rules

The calculation of an RfD, as in 2.2, is normally regarded as risk assessment. This means that, according to the received view, it is supposed to be a scientific or at least science-based, and as such non-normative. One understanding of the safety factor rule is empirical. The NOAEL or BMD values are results from rather straightforward experimental procedures. If we consider the RfD to be a non-normative concept, then the uncertainty factor rule is relatively innocuous, as it is not to be understood as action guiding. It merely describes a manner of using words. However, it certainly seems as if an element of normativity has snuck into the idea of an RfD, as can be seen in the quote given earlier: “... unlikely [our emphasis] to put humans at appreciable [our emphasis] risk.”. It is arguably a normative issue what we consider to be unlikely, ⁵ not to mention when a risk is appreciable, since it appeals to the intuition that we need not care about unlikely or unappreciable risks. So, if the RfD is interpreted normatively, we have something that isn’t quite as innocuous, namely the claim that finding a certain experimental value and dividing it by suitable factors presents us with a dose that is at least prima facie nothing to worry about.

The safety factor rule in 2.2 is more openly normative since it speaks of design values which according to Ditlevsen and Madsen (2004) should be interpreted in such a way that a structure is “just sufficiently safe” if it is constructed using design values ( Ditlevsen and Madsen, 2004 , p.22). To build a structure with parameters implying safety beyond that provided by building with design values is, according to such a view, going over and above what can reasonably be required. It is supererogatory if you will.

The normativity of safety factor rules makes them controversial, but it is also the very thing that makes them useful, not only in practical reasoning during the risk management and assessment processes, but also in normative reasoning about the results of risk management and assessment.

Practical and theoretical reasoning with safety factor rules

The following is a “just so” account of the role played by safety factor rules in toxicological risk assessment and structural engineering. With “just so” we mean to say that the account should not necessarily be taken as an empirical conjecture. It is more of a demonstration of possibility, showing how safety factor rules and definitions can be used in inferences. This is sufficient for answering the question of whether we can make sense of the distinction between assessment safety factor rules and management safety factor rules.

Reasoning with the toxicological safety (uncertainty) factor rule

To recap, the safety factor rule mentioned in 2.2 was the following:

NOAEL Rule: A dose less than NOAEL/U is unlikely to put humans at appreciable risk

In toxicological risk assessment, the “just so” story starts out with an intention to find an RfD, or a dose unlikely to put humans at appreciable risk. The NOAEL Rule tells us that a sufficient means to finding such a dose is to find a NOAEL and divide by a suitable U. This corresponds to a “leftward” motion in the research-assessment-management model, from a question belonging to risk assessment to a question for research – to find a NOAEL.

However, the motion for which the rule can be used is also a “rightward” one. When an answer has been provided by research, such as the specific value of a NOAEL, we can use the NOAEL Rule to infer an RfD, by dividing the NOAEL by U.

The first reasoning that makes use of the rule is a piece of practical reasoning from an intention to find out something necessary for risk assessment to an intention to do certain research. The second piece of reasoning is theoretical and takes us from a research answer to a risk assessment answer. Since both these pieces of reasoning can be nested within a risk management process it could be argued that in such a nested case, any safety factor used is possibly done so, in a sense, in an encapsulating risk management process.

Reasoning with the engineering safety factor rule

As above, we will recap the safety factor rule mentioned earlier:

Simplified Partial Safety Factor Rule: S _i γ _Si ≤ R _j /γ _Rj

While risk assessment in toxicology is about finding “safe” doses, risk assessment in structural engineering can be seen as finding “safe” designs or evaluating designs with respect to safety. Just as the NOAEL Rule in 4.2.1, the Simplified Partial Safety Factor Rule, with given safety factors, tells us that if we want to find a sufficiently safe design we need to find characteristic values (reasoning “leftwards” from intentions for risk assessment to intentions for research). And, as above, the other direction of reasoning is possible when we are faced with a structure with certain characteristic values for materials given from research. We can then infer whether the structure is safe or unsafe by calculating the “implied” safety factor and compare it to our code.

Comments

The safety factor rules can arguably be used in both assessment and management because of the nesting of management, assessment and research processes, as well as the dual “directions” of reasoning made possible by the rules. Thus, a distinction between management and assessment safety factor rules and definitions does not lie in when they can be used. Might it lie instead in when they should be used? Again, nesting and dual use present problems, for say e.g. that we create a compound factor, multiplying all the needed factors – be they considered assessment factors, management factors or other – that will takes us from a research result to a risk management decision. Is the calculation with such a compound factor to be seen as management, assessment or what? If the subfactors are justified for use separately, surely it will be justified to use a compound factor that is not easily identified as either an assessment or management factor. A remaining possibility is that assessment safety factor rules are used only during the risk assessment phase, and that management safety factor rules are used only during the risk management phase, but the plausibility of the dual directions of reasoning seem to speak against this. Further, nesting again presents a problem of placing a certain event squarely in only one of the research, assessment and management categories.

One possible reaction to the accounts of 4.2.1 and 4.2.2 is that they are simple, and perhaps too simple. This is, we would argue, precisely the point. Our conjecture is that the use of safety factor rules owes much to the simplicity of the reasoning involved. What can be added at this point is that a simple rule with simple reasoning can fail to do what it is supposed to do, and that a far more complex rule might do the job better, ⁶ if the job is understood as enabling accurate conclusions. Banal as it may seem, safety factor rules are often a trade-off between simplicity of reasoning and accuracy of conclusions, with the prime difficulty being that we cannot normally say how exactly the trade-off looks.

Discussion

Valid inferences and correct results

As mentioned in 4.2, safety factor rules play the role of “bridge hypotheses” and are the answer to science policy issues ( RIAP, 1994 ). They enable agents who believe in them to make valid inferences about important issues, where valid is to be understood as logically valid. Logically valid inferences, however, do of course not guarantee that the conclusions derived are correct. Take the racist inference rule of “If someone has a different skin color than you do, that person is unintelligent”. Conclusions derived about the intelligence of others with the help of this rule may be logically valid, although they will often be inaccurate.

Do safety factor rules go too far?

Commonly used safety factor rules are generally not thought of as necessary for safety, but rather as sufficient since they are often thought of as conservative or cautious. This suggests that if we knew more we could act with lower regard for the safety factor rule, and still be safe. One criticism that can be voiced against the use of safety factor rules relates to this, and it is that they enable unwarranted conclusions and might thus not, in fact, be sufficient for safety. In a choice between using a safety factor rule and statistical methods, one can ask what conclusions will be enabled by each approach. Let us assume that we are doing measurements on rats examining the prevalence of blindness resulting from exposure to some substance S. The results from the study indicate that the NOAEL is 4 mg/kg bw and that the highest dose not provoking blindness at 0.95 confidence level is the range 2-7.3 mg/kg bw. A further study on the general chemical sensitivity of rats as compared to humans gives, say, that humans are 0.22 - 13 times more sensitive per kg bw at 0.95 confidence. This gives us a range from 0.148 to 33.2 mg/kg bw for the highest dose not provoking blindness at confidence ≥ 0.9. ⁷ The result from the default uncertainty factor rule is that a dose under 0.4 mg /kg bw is safe using an interspecies factor of 10. Now, although this example is entirely fictional and many details have been omitted, we would argue that this is how different the conclusions from the statistical approach and the safety factor approach can be, even given the same information. In fact, the less statistical information we have, the more divergent results will be since intervals with a fixed confidence level will become larger.

If the conclusions made possible by safety factor rules outstrip those made possible by statistical methods, those “extra” conclusions (such as altering the “safe” interval) will be unwarranted according to the confidence level chosen for the statistical analysis. One could, for example, experiment with confidence levels to see at which point the conclusions warranted by a safety factor rule become warranted by the statistical analysis. In this regard it cannot be the case that more “allowing” safety factor rules can replace statistical analysis without a loss in epistemic reliability, that is, without implying larger epistemological risks. Obviously, if we chose to have a very low confidence level in the statistical analysis virtually any conclusion can be “supported” by the analysis.

Evolution of safety factors

There is an interesting difference between safety factor rules that have a long history and statistical analyses based on more recent studies or compilations of data, which might affect how safety rules unsupported of statistics are viewed. It is a difference similar to that between batch and online learning in Computer Science. Online learning is myopic in that it gives incremental output to incremental input, while batch learning takes into account all the available input. ⁸ To see how they are different, imagine that you have one hour to find the highest point you can in a hilly landscape. Before beginning the task you are blindfolded, so the only way of finding your way is by moving around the landscape sensing the incline. If you wanted to solve the problem in an “online” way you would at each point in your “optimizing walk” decide where to go next and hope that that next step would take you to the highest point, and after each step forget all about where you had been previously. After one hour you simply stop. Solving it in a more “batch”-like way would be to first walk around a while, collecting data by memorizing the entire walk, and then try to infer where the highest point lies. Batch processing requires more memory, namely enough for the entire sequence of input, while online processing has the downside of not being repeatable or open to scrutiny unless the same sequence of input is presented again. ⁹

In a similar way, we can see that safety factor rules in some areas have been around for a long time, and some of these factors have been incrementally changed over time, presumably as reactions to events related to their use or new research results. The values they do have may be supported by good reason, although the details of those reasons are sometimes lost. Thinking along these lines relates to Ditlevsen’s (1997) discussion about a “superior authority” within a country or union of countries that, even in cases where codes have not been calibrated using modern statistical methods, decides what designs or codes are to be considered optimal. An interesting question then becomes how good statistical data we need before deciding to alter an “online” safety factor rule in a batch-like fashion. It is not a question to which we have an answer, but it suffices to acknowledge for the moment that it presents a serious complication for normative evaluation of safety factors that are not supported by readily available statistical data.

Safety factor rules are responses to science policy issues

The terms science policy issues and science policy decisions can be used to further explain safety factor rules. Here we need to distinguish between provable and unprovable risks. The following quote from Choices in Risk Assessment (1994) gives a characterization:

Provable risks can be measured or observed directly and include actuarial risks such as those associated with highway or air travel accidents. In contrast, other risks – such as those associated with low-doses of radiation or exposure to chemicals in the environment – are often too small to be measured or observed directly with existing scientific methods and available resources. Additionally, specific health and environmental effects are often difficult to attribute to specific causes because other competing causes cannot be excluded with reasonable certainty. Such risks are unprovable. (p. 241)

The next quote gives the definition of science policy issues and decisions:

When risk assessment is used to estimate unprovable risks, these gaps and uncertainties [in scientific knowledge, data and method] become science policy issues. Both risk assessors and risk managers make science policy decisions in order to bridge the gaps and uncertainties. Thus, science policy decisions enable the estimation of unprovable risks. (ibid, p. 241)

Even though Choices in Risk Assessment focuses on chemical risks, the idea is quite general. In other words, when we lack solid information, we have to make educated guesses, given that we must provide an answer . In the face of uncertainty we have two basic ways to go: defer judgment or guess. Science policy questions are questions of how we ought to guess under the difficult circumstances mentioned, given that deferring judgment is out of the question. Such guesses do not come without a cost (of sorts). Whatever answer we provide will have a less than ideal (or as is normally the case, less than scientific) reliability, and acting upon it means taking what Sahlin and Persson (1994) call an epistemic risk . This does not imply that we are taking an outcome risk (doing something that has possible unwanted outcomes) of a certain magnitude, but it does imply that we are uncertain about the magnitude of outcome risk we are in fact running. Thus, recognizing that safety factor rules are, in many cases, responses to science policy issues tells us that they are not standards with which we can rest easy.

Conclusions

The questions we set out to answer were “How are safety factor rules used?”, “Why are they used?”, “When are they used?” and “What is their place in decision theory?”.

The answer to the first of these is that safety factor rules are used in at least two forms of reasoning: (i) “leftwards” practical reasoning about sufficient information gathering given needs in risk management and risk assessment towards research and (ii) “rightwards” theoretical reasoning in the direction from research results, through risk assessment results to risk management decisions. That the same rule can be used for both these forms of reasoning was presented as one of two arguments against dividing safety factors into “risk reduction factors” (or management factors) and assessment factors, the other being the possible “nesting” of research, assessment and management processes.

Concerning why safety factors are used, there are several different explanations. One is simply that in certain situations of radical uncertainty we have made a meta decision that we nevertheless must provide answers to certain questions, such as “Is this structure safe?” or “Is this dose safe?”, and that reliance on either statistical data or the evolutionary process that produced a certain safety factor rule is strong enough. We have, often implicitly, deemed the epistemic risk inherent in using the safety factor rule acceptable. For other situations, where more precise calculations can be made, using safety factors is a simple alternative, a heuristic, and when carefully chosen the safety factor rule can be equivalent, or approximately equivalent, to more complex procedures for a suitably restricted range of cases. In certain cases, when safety factor rules are used unreflectively, one may of course say that they are used because of tradition or simply because regulations force us to, since their use is at times mandatory.

The “When” question has been answered, at least partially, but something can be added. The situations in which the rules are used are situations of varying degrees of uncertainty. Were there no uncertainty, safety factor rules would be superfluous. However, just uncertainty is not enough to motivate their use. The agents using safety factors are generally resource constrained. Safety factor rules allow for resource-bounded decisions to be made systematically, making behavior, at least in principle, open to deliberate revision.

Finally, when it comes to their relation to decision theory, safety factor rules should be seen more as decision methods, tightly connected to highly specific circumstances such as “driving on the highway” or “designing a structural component”, than as criteria of rightness. They encode trade-offs between various values at stake and beliefs about the world, but on a superficial level they are satisficing with respect to safety, in the sense that they tell us when something is “sufficiently safe”. However, since the precise formulation of a safety factor rule is often a matter of science policy decision-making, this tells us that any such statement of sufficient safety is provisional.

Acknowledgments

This paper is part of a project financed by the Swedish Research Council. The authors would like to thank Fred Nilsson and Sven Ove Hansson for valuable comments on earlier version of this paper.

Notes

1 Several other key dose values are or have been in use. Among these we find tolerable daily intake (TDI), acceptable daily intake (ADI) and provisional tolerable weekly intake (PWTI) ( Herrman and Younes, 1999 ).

2 This assumption is not uncontroversial. There is a discussion in toxicology about the nature of hormesis ; when a substance gives rise to higher rates of a certain adverse effect at a low dose than it does at a higher dose. See, for example, Calabrese et al. (1999) .

3 The distinction between decision phases in this way is Simon’s (1977) .

4 “Intending to act is as close to acting as reasoning alone can get us, so we should take practical reasoning to be reasoning that concludes in an intention.” (p. 1, Broome, 2002 )

5 Is probability 0.5 unlikely? Is 10 ^-3 ? Or need we go as far as 10 ^-6 ? There is serious vagueness here and thus ample room for a broad range of values to affect interpretation.

6 The work of Gigerenzer and Todd suggests that simple rules may in fact do very well under suitable circumstances. See, for example, Gigerenzer and Todd (1999) .

7 According to Bonferroni’s inequality.

8 For a discussion of batch and online learning, see for example Barkai et al. (1995) .

9 Many algorithms can be formulated in equivalent variants, either online or batch. This equivalence is in terms of eventual results, not in such things as memory requirements or execution speed.

References

Barkai, N., Seung, H.S. and Sompolinsky, H. 1995, “Local and Global Convergence of On-Line Learning”, Physical Review Letters 75(7):1415-1418.

Boverket 2003, Regelsamling för konstruktion – Boverkets konstruktionsregler, BKR byggnadsverkslagen och byggnadsverksförordningen , Boverket.

Brand, K.P., Rhomberg, L. and Evans, J.S. 1999, “Estimating noncancer uncertainty factors: are ratios NOAELs informative?”, Risk Analysis 19(2):295-308.

Broome, J. 2002, “Practical Reasoning” in Bermùdez, J. and Millar, A. (2003) Reason and Nature: Essays in the Theory of Rationality, Oxford University Press.

Calabrese, E.J., Baldwin, L.A. and Holland C.D. 1999, “Hormesis: A Highly Generalizable and Reproducible Phenomenon With Important Implications for Risk Assessment”, Risk Analysis 19(2):261-281.

Ditlevsen, O. 1997, “Structural reliability codes for probabilistic design – a debate paper based on elementary reliability and decision analysis concepts”, Structural Safety 19(3):253-270.

Ditlevsen, O. and Madsen, H.O. 2004, Structural Reliability Methods , Internet Edition 2.2.1, http://www.mek.dtu.dk/staff/od/books.htm.
Note :  The url provided above returned invalid results.
Relevant information may be found at the following link:
http://www.skk.mek.dtu.dk/English/Publikationer/Publikaitoner-2005.aspx?lg=showcommon&id=182670

Dourson, M.L., Felter, S.P and Robinson, D. 1996, “Evolution of Science-Based Uncertainty Factors in Noncancer Risk Assessment”, Regulatory Toxicology and Pharmacology 24(2):108-120.

Gaylor, D.W. and Kodell, R.L. 2000, “Percentiles of the product of uncertainty factors for establishing probabilistic reference doses”, Risk Analysis 20(2):245-250.

Gaylor, D.W. and Kodell, R.L. 2002, “A Procedure for Developing Risk-Based Reference Doses”, Regulatory Toxicology and Pharmacology 35:137-141.

Gayton, N., Mohamed, A., Sorensen, J.D., Pendola, M. and Lemaire, M. 2004, “Calibration methods for reliability-based design codes”, Structural Safety 26(1):91-121.

Gigerenzer, G. and Todd, P.M. 1999, Simple Heuristics That Make Us Smart, Oxford University Press.

Herrman, J.L. and Younes, M. 1999, “Background to the ADI/TDI/PTWI”, Regulatory Toxicology and Pharmacology 30:S109-S113.

Kalberlah, F., Föst, U. and Schneider, K. 2002, “Time Extrapolating and Interspecies Extrapolation for Locally Acting Substances in case of Limited Toxicological Data”, Annals of Occupational Hygiene 2:175-185.

Levi, I. 1981, The Enterprise of Knowledge , The MIT Press.

National Research Council 1996, Science and Judgment in Risk Assessment , Taylor & Francis.

RIAP 1994, Choices in Risk Assessment, Sandia National Laboratories.

Richardson, H.S. 2004, “Satisficing: Not Good Enough” in Byron, M. (2004) Satisficing and Maximizing, Cambridge University Press.

Sahlin, N-E. and Persson, J. 1994, “Epistemic Risk: The Significance of Knowing What One Does Not Know” in Bremer, B. and Sahlin, N-E. 1994, Future Risks and Risk Management, Kluwer.

Simon, H.A. 1972, “Theories of Bounded Rationality” in Simon, H.A. 1982, Models of Bounded Rationality: Behavioral Economics and Business Organization, The MIT Press.

Simon, H.A. 1976, “From Substantive to Procedural Rationality” in Simon, H.A. 1982, Models of Bounded Rationality: Behavioral Economics and Business Organization, The MIT Press.

Simon, H.A. 1977, The New Science of Management Decision, Prentice-Hall.