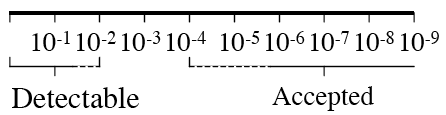SPT v8n1 - Philosophical Perspectives on Risk

Philosophical Perspectives on Risk

Sven Ove Hansson
Royal Institute of Technology, Stockholm

The Concept of Risk

In non-technical contexts, the word "risk" refers, often rather vaguely, to situations in which it is possible but not certain that some undesirable event will occur. In technical contexts, the word has many uses and specialized meanings. The most common ones are the following:

(1)	risk = an unwanted event which may or may not occur.
(2)	risk = the cause of an unwanted event which may or may not occur.
(3)	risk = the probability of an unwanted event which may or may not occur.
(4)	risk = the statistical expectation value of unwanted events which may or may not occur.
(5)	risk = the fact that a decision is made under conditions of known probabilities ("decision under risk")

Examples: Lung cancer is one of the major risks (1) that affect smokers. Smoking also causes other diseases, and it is by far the most important health risk (2) in industrialized countries. There is evidence that the risk (3) of having one's life shortened by smoking is as high as 50%. The total risk (4) from smoking is higher than that from any other cause that has been analyzed by risk analysts. The probabilities of various smoking-related diseases are so well-known that a decision whether or not to smoke can be classified as a decision under risk (5).

The third and fourth of these meanings are the ones most commonly used by engineers. The fourth, in particular, is the standard meaning of "risk" in professional risk analysis. In that discipline, "risk" often denotes a numerical representation of severity, that is obtained by multiplying the probability of an unwanted event with a measure of its disvalue (negative value). When, for instance, the risks associated with nuclear energy are compared in numerical terms to those of fossil fuels, "risk" is usually taken in this sense. Indeed, all the major variants of technological risk analysis are based on one and the same formal model of risk, namely objectivist expected utility , that combines objectivist probabilities with objectivist utilities ( Hansson 1993 ). By an objectivist probability is meant a probability that is interpreted as an objective frequency or propensity, and thus not (merely) as a degree of belief. Similarly, a utility assignment is objectivist if it is interpreted as (a linear function of) some objective quantity.

It is often taken for granted that this sense of risk is the only one that we need. In studies of "risk perception," the "subjective risk" reported by the subjects is compared to the "objective risk," which is identified with the value obtained in this way. However, from a philosophical point of view it is far from obvious that this model of risk captures all that is essential. I will try to show why it is insufficient and how it should be supplemented. In doing this, I will also show how the issue of risk gives rise to important new problems for several areas of philosophy, such as epistemology, philosophy of science, decision theory and—in particular—ethics. Let us begin with epistemology.

Epistemology

In all the senses of "risk" referred to above, the use of this term is based on a subtle combination of knowledge and uncertainty. When there is a risk, there must be something that is unknown or has an unknown outcome; hence there must be uncertainty. But for this uncertainty to constitute a risk for us, something must be known about it. This combination of knowledge and lack thereof contributes to making issues of risk so difficult to come to grips with in practical technological applications. It also gives rise to important philosophical issues for the theory of knowledge.

Risk and Uncertainty

In decision theory, lack of knowledge is divided into the two major categories "risk" and "uncertainty". In decision-making under risk, we know what the possible outcomes are and what are their probabilities. ¹ Perhaps a more adequate term for this would be "decision-making under known probabilities". In decision-making under uncertainty, probabilities are either not known at all or only known with insufficient precision. ²

Only very rarely are probabilities known with certainty. Therefore, strictly speaking, the only clear-cut cases of "risk" (known probabilities) seem to be idealized textbook cases that refer to devices such as dice or coins that are supposed to be known with certainty to be fair. More typical real-life cases are characterized by (epistemic) uncertainty that does not, primarily, come with exact probabilities. Hence, almost all decisions are decisions "under uncertainty". To the extent that we make decisions "under risk," this does not mean that these decisions are made under conditions of completely known probabilities. Rather, it means that we have chosen to simplify our description of these decision problems by treating them as cases of known probabilities.

It is common to treat cases where experts have provided exact probabilities as cases of decision-making under risk. And of course, to give just one example, if you are absolutely certain that current estimates of the effects of low-dose radiation are accurate, then decision-making referring to such exposure may be decision-making under risk. However, if you are less than fully convinced, then this too is a case of decision-making under uncertainty. Experts are known to have made mistakes, and a rational decision-maker should take into account the possibility that this may happen again. Experts often do not realize that for the non-expert, the possibility of the experts being wrong may very well be a dominant part of the risk (in the informal sense of the word) involved e.g. in the use of a complex technology. When there is a wide divergence between the views of experts and those of the public, this is certainly a sign of failure in the social system for division of intellectual labor, but it does not necessarily follow that this failure is located within the minds of the non-experts who distrust the experts. It cannot be a criterion of rationality that one takes experts for infallible. Therefore, even when experts talk about risk, and give exact probability statements, the real issue for most of us may nevertheless be one of epistemic uncertainty.

The Reduction of Uncertainty

One possible approach to all this epistemic uncertainty, and perhaps at first hand the most attractive one, is that we should always take all uncertainty that there is into account, and that all decisions should be treated as decisions under epistemic uncertainty. However, attractive though this approach may seem, it is not in practice feasible, since human cognitive powers are insufficient to handle such a mass of unsettled issues. In order to grasp complex situations, we therefore reduce the prevailing epistemic uncertainty to probabilities ("There is a 90% chance that it will rain tomorrow") or even to full beliefs ("It will rain tomorrow"). ³ This process of uncertainty reduction, or "fixation of belief" ( Peirce 1934 ), helps us to achieve a cognitively manageable representation of the world, and thus increases our competence and efficiency as decision-makers.

Another possible approach to uncertainty is provided by Bayesian decision theory. According to the Bayesian ideal of rationality, all statements about the world should have a definite probability value assigned to them. Nonlogical propositions should never be fully believed, but only assigned high probabilities. Hence, epistemic uncertainty is always reduced to probability, but never to full belief. The resulting belief system is a complex web of interconnected probability statements ( Jeffrey 1956 ).

In practice, the degree of uncertainty-reduction provided by Bayesianism is insufficient to achieve a manageable belief system. Our cognitive limitations are so severe that massive reductions to full beliefs (certainty) are indispensable if we wish to be capable of reaching conclusions and making decisions. ⁴ As one example of this, since all measurement practices are theory-laden, no reasonably simple account of measurement would be available in a Bayesian approach ( McLaughlin 1970 ). On the other hand, Bayesianism cannot either account for the fact that we also live with some unreduced epistemic uncertainties.

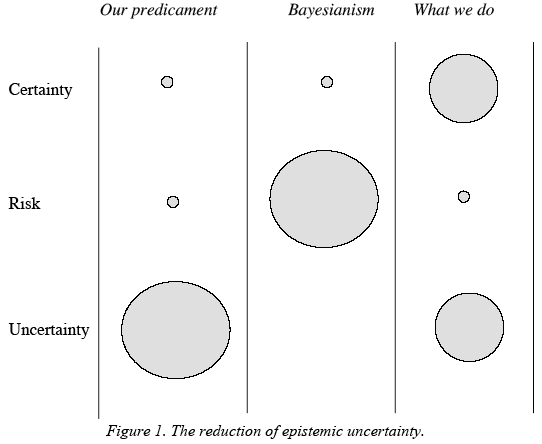
Figure 1. The reduction of epistemic uncertainty. The left column represents our predicament as it looks like in practice. Most of our beliefs are uncertain. Only in few cases do we have certainty, or precise probabilistic knowledge ("risk"). The middle column represents the Bayesian simplification, in which uncertainty is reduced to risk. The right column represents the simplification that we perform in practice, treating many of our uncertain beliefs provisionally as if they were certain knowledge.

In my view, it is a crucial drawback of the Bayesian model that it does not take into account the cognitive limitations of actual human beings. Of course, we may wish to reflect on how a rational being with unlimited cognitive capabilities should behave, but these are speculations with only limited relevance for actual human beings. A much more constructive approach is to discuss how a rational being with limited cognitive capabilities can make rational use of these capabilities.

In practice, in order to grasp complex situations, we need to reduce the prevailing epistemic uncertainty not only to probabilities but also to full beliefs. Such reductions will have to be temporary, so that we can revert from full belief to probability or even to uncertainty, when there are reasons to do this. This is how we act in practice, and it also seems to be the only sensible thing to do, but we do not yet have a theory that clarifies the nature of this process ( See Figure 1 ).

There are important lessons for risk research to draw from this. In risk analysis, it is mostly taken for granted that a rational individual's attitude to uncertain possibilities should be representable in terms of probability assignments. Due to our cognitive limitations, this assumption is not always correct. In many instances, more crude attitudes such as "This will not happen" or "It is possible that this may happen" may be more serviceable. Transitions between probabilistic and non-probabilistic attitudes to risk seem to be worth careful investigations, both from an empirical and a normative point of view. I believe, for instance, that such transitions are common in the process of technological design. An engineer designing a new product typically questions some parts of the construction at a time, while at least temporarily taking the reliability of the other parts for granted. This way of reasoning keeps uncertainty at a level at which it can be handled.

The process of uncertainty reduction is not a value-free or "purely epistemic" process. We are less reluctant to ignore remote or improbable alternatives when the stakes are high. Suppose that when searching for mislaid ammunition, I open and carefully check a revolver, concluding that it is empty. I may then say that I know that the revolver is unloaded. However, if somebody then points the revolver at my head asking: "May I then pull the trigger?," it would not be unreasonable or inconsistent of me to say "No," and to use the language of probability or uncertainty when explaining why. In this case, we revert from full belief to uncertainty when the stakes involved are changed.

Given our limited cognitive capabilities, this behavior appears to be quite rational. We have to reduce much of the prevailing uncertainty to (provisional) full beliefs. In order to minimize the negative consequences of these reductions, considerations of practical value must have a large influence on the reduction process. Once we take considerations of risk and uncertainty into account, it will be clear that epistemology cannot be independent of moral values or other practical values. This connection between epistemology and ethics is one of the major philosophical lessons that we can learn from studies of risk.

Philosophy of Science

In science, as well as in everyday life, cognitive limitations make a reduction process necessary. The corpus of scientific knowledge consists of those standpoints that we take, in science, for provisionally certain. It is, in fact, the outcome of an epistemic reduction process. However, there is one important difference between the scientific reduction process and that of everyday life: Science programmatically ignores considerations of practical value. More precisely, contrary to everyday reasoning, the scientific process of uncertainty-reduction is bound by rules that (at least ideally) restrict the grounds for accepting or rejecting a proposition to considerations unrelated to practical consequences. There are good reasons for this restriction. As decision-makers and cognitive agents with limited capacity, we could hardly do without a general-purpose, intersubjective, and continually updated corpus of beliefs that can for most purposes be taken to be the outcome of reasonable reductions of uncertainty.

The Burden of Proof

When determining whether or not a scientific hypothesis should be accepted for the time being, the onus of proof falls squarely to its adherents. Similarly, those who claim the existence of an as yet unproven phenomenon have the burden of proof. These proof standards are essential for both intra- and extrascientific reasons. They prevent scientific progress from being blocked by the pursuit of all sorts of blind alleys. They also ensure that the scientific corpus is reliable enough to be useful for (most) extra-scientific applications. Nevertheless, the proof standards of science are apt to cause problems whenever science is applied to practical problems that require standards of proof other than those of science. Examples of this are readily found in risk-related decision-making. It would not seem rational—let alone morally defensible—for a decision-maker to ignore all preliminary indications of a possible danger that do not amount to full scientific proof. Therefore, such decisions have to be based on scientific knowledge, but yet apply proof standards that differ from those of science.

Figure 2. The use of scientific data for policy purposes.

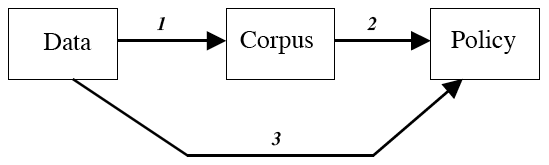
The implications of this are shown in Figure 2. Scientific knowledge begins with data that originate in experiments and other observations. Through a process of critical assessment, these data give rise to the scientific corpus (arrow 1). Roughly speaking, the corpus consists of those statements that could, at the time being, legitimately be made, without reservation, in a (sufficiently detailed) textbook. The obvious way to use scientific information for policy purpose is to use information from the corpus (arrow 2). For many purposes, this is the only sensible thing to do. However, in the context of risk it may have unwanted consequences to rely exclusively on the corpus. Suppose that there are suspicions, based on relevant but insufficient scientific evidence, that a certain chemical substance is dangerous to human health. Since the evidence is not sufficient to warrant an addition to the scientific corpus, this information cannot influence policies in the "standard" way, arrows 1 and 2. However, the evidence may nevertheless be sufficient to warrant changes in technologies in which that chemical is being used. We want, in cases like this, to have a direct way from data to policies (arrow 3).

However, in order to avoid unwarranted action due to misinterpreted scientific data, it is essential that this direct road from data to policy be guided by scientific judgment in essentially the same way as the road from data to corpus. The major differences between the assessments represented by arrows 1 and 3 is that in the latter case, the level of required proof is adjusted to policy purposes. Scientists often have difficulties in coping with this situation. Engineers are more used to it. For more than a century, they have adjusted burdens and levels of proof to required levels of safety.

But we should not underestimate the problems involved in adjusting proof levels in the way required in the process represented by arrow 3. For one thing, new methods of statistical evaluation are often needed ( Hansson 1995 ; 2002 ). Furthermore, we will have to deal with a proliferation problem: If we change the required levels of proof for certain issues, such as the presence of health risks, then we also have—at least in principle—to adjust the standards of proof for the more basic science on which we base our conclusions. Hence, suppose that we wish to apply, for policy purposes, adjusted standards of evidence to issues in toxicology. This will require a complete reform of the standards of evidence that will not only affect the interpretation of individual results in toxicology, but also our views on more basic biological phenomena. As an example, if our main concern is not to miss any possible mechanism for toxicity, then we must pay serious attention to possible metabolic pathways for which there is insufficient proof. Such considerations in turn have intricate connections with various issues in biochemistry, and ideally, we should perform a massive reappraisal of an immense mass of empirical conclusions, hypotheses, and theories. Presumably, this reappraisal could be performed by an ideal Bayesian subject, but it is far beyond the reach of human scientists of flesh and blood. Each of us has access only to small parts of the entire corpus of knowledge on which modern science is based, and this corpus has been shaped by innumerable fixations of belief that have accorded with ordinary scientific standards of proof. Partial adjustments can be made, but there is no way to realign the entire corpus to make it accord with standards of evidence other than those that have guided its development. Hence, although the scientific corpus has been developed as a source of general-purpose knowledge, it is not perfectly adjusted to all the purposes for which we need scientific knowledge. This is another basic philosophical insight that can be gained when we take issues of risk into serious consideration.

Limits of Scientific Knowledge—Indetectable Effects

Ideally, we want our decisions to be based on direct observations, rather than on more indirect conclusions. But how far can this be achieved? In issues of risk there are rather strong limits on what can be directly observed. Many risks are in fact indetectable. Let me explain why.

By the detection of a phenomenon I will mean that its existence is ascertained through some empirical observation that is only possible when the phenomenon exists. A phenomenon may be indetectable although there are convincing theoretical reasons to believe that it exists. If we add a small amount of hot water to a lake, the effect may be completely indetectable ex post. Whatever difference in temperature that we can measure is indistinguishable from random variations. But we know from elementary physics that our action has increased the temperature of the lake. This effect is knowable in spite of being indetectable.

Risks affecting human beings can be detectable either on the individual or only on the collective level ( Hansson 1999b ). The following hypothetical example can be used to clarify the distinction. There are three chemical substances A, B, and C, and 1000 persons exposed to each of them. Exposure to A gives rise to hepatic angiosarcoma among 0.5 % of the exposed. Among unexposed individuals, the frequency of this disease is very close to 0. Therefore, the individual victims can be identified. This effect is detectable on the individual level.

Exposure to B causes a rise in the incidence of leukemia from 1.0 to 1.5 %. Hence, the number of victims will be the same as for A, but although we know that about 10 of the about 15 leukemia patients would also have contracted the disease in the absence of exposure to the substance, we cannot find out who these ten patients are. The victims cannot be identified. On the other hand, the increased incidence is clearly distinguishable from random variations (given the usual criteria for statistical significance). Therefore, the effect of substance B is detectable on the collective (statistical) but not on the individual level.

Exposure to C leads to a rise in the incidence of lung cancer from 10.0 to 10.5 %. Again, the number of additional cancer cases is the same as for the other two substances. Just as in the previous case, individual victims cannot be identified. In addition, since the difference between 10.0 and 10.5 % is indistinguishable from random variations, the effects of this substance are indetectable even on the collective level.

We can therefore distinguish between effects that are completely indetectable, like the effects of substance C, and effects that are only individually indetectable, like those of substance B.

This example can help us to understand two important issues in risk management. The first of these is whether or not there is an ethical difference between cases A and B. This problem has been discussed, mostly with other types of examples, under the name of the discrimination of statistical victims ( Weale 1979 ; Trachtman 1985 ). In case A, the victims are identified whereas in case B, they are unidentified ("statistical"). In actual social policies, statistical victims are often given a much lower priority than identified victims. Our societies are willing to pay much more to save known individuals in danger or distress than to reduce mortality or morbidity by measures not directed at identifiable individuals. Heart transplant candidates and trapped miners are examples of the former, whereas most measures undertaken for preventive purposes "only" save statistical lives, and receive much less funding per saved life. However, since the level of human suffering seems to be the same in both cases, it is not a trivial task to defend this difference in treatment from an ethical point of view. ⁵

The other problem is whether or not completely indetectable effects, such as those in case C, are at all a matter of concern. In environmental policies it has often been implicitly assumed that what cannot be detected cannot be a matter of concern. Occasionally, this has also been explicitly stated. Hence, the Health Physics Society wrote in a position statement:

...[E]stimate of risk should be limited to individuals receiving a dose of 5 rem in one year or a lifetime dose of 10 rem in addition to natural background. Below these doses, risk estimates should not be used; expressions of risk should only be qualitative emphasizing the inability to detect any increased health detriment (i.e., zero health effects is the most likely outcome). (Health Physics Society 1996)

In my view, this is an untenable standpoint. A major reason for this is that indetectable effects may be much larger than what most of us are aware of. To simplify the discussion, let us focus on lifetime risks of lethal effects. As a rough rule of thumb, epidemiological studies can reliably detect excess relative risks only if they are about 10 % or greater. For the more common types of lethal diseases, such as coronary disease and lung cancer, lifetime risks are of the order of magnitude of about 10 %. Therefore, even in the most sensitive studies, an increase in lifetime risk of the size 10-2 (10 % of 10 %) or smaller may be indetectable (i.e. indistinguishable from random variations). In animal experiments we have similar experimental problems, and in addition problems of extrapolation from one species to another.

How small health effects should be of concern to us? Many attempts have been made to set a limit of concern, expressed either as "acceptable risk" or "de minimis risk". Most of us would agree that if a human population is exposed to a risk factor that will, statistically, kill one person out of 109, then that risk is not an issue of high priority. Arguably, it would be no disaster if our risk assessment methods are insufficient to discover risks of that order of magnitude. On the other hand, most of us would consider it a serious problem if a risk factor kills one person out of 100 or 1000. The most common proposals for limits of concern for lethal risks are 1 in 100 000 and 1 in 1000 000. It is difficult to find proposals above 1 in 10 000. These values are of course not objective or scientific limits; I just report what seems the be levels at which lethal risks are accept ed (as distinguished from accept able ).

Figure 3. The ethical gap.

We therefore have what may be called an ethical gap , a gap between those (probabilistic) risk levels that are scientifically detectable and those that are commonly regarded to be ethically acceptable or at least of minor concern. This ethical gap, illustrated in Figure 3, has the breadth of 2-4 orders of magnitude. This gap is surprisingly unknown among risk assessors. One of the several practical issues that should be discussed, based on this knowledge, is the use of uncertainty factors ("safety factors") to bridge this gap. For a concrete example, if we consider the gap to be three orders of magnitude (i.e. if we accept risks smaller than 10-5, then an uncertainty (safety) factor of 1000 is required to bridge the gap.

Ethics and Decision Theory

The above discussions of risk from the perspectives of epistemology and philosophy of science have shown how the issue of risk creates strong connections between these respective disciplines and moral philosophy (ethics). Let us now turn to moral philosophy itself.

The Division of Labor Between Ethics and Decision Theory

Moral philosophy is not the only philosophical subdiscipline that tries to answer the question "What should we do?". This is also done by another subdiscipline of philosophy, namely decision theory. However, according to the received view, these two subdisciplines do not compete, since they cover disjoint and clearly demarcated subject areas. Decision theory is assumed to take values for given and add no new values. It is therefore, in a sense, seen as morally neutral. In issues of risk, decision theory takes value assignments for deterministic cases for given, and derives from them instructions for rational behavior in an uncertain, unpredictable, and indeterministic world. Another way to express this is that, given preferences over deterministic alternatives, decision theory derives preferences over indeterministic alternatives.

Suppose, for instance, that moral considerations have led us to attach well-determined values to two outcomes X and Y. Then decision theory provides us with a value to be attached to mixed options such as 50%-chance-of-Xand- 50%-chance-of-Y. The crucial assumption is that, given well-determined probabilities, and well-determined values of the basic, non-probabilistic alternatives X and Y, the values of mixed options can be derived . In other words, probabilities and the values of non-probabilistic alternatives are assumed to completely determine the value of probabilistic alternatives. This is the conventional wisdom, so conventional that it is seldom stated explicitly. I believe it to be grossly misleading.

It is clear that we assign values to (or have preferences over) both deterministic and indeterministic objects of value. It is also reasonable to expect that there be correlations and connections between these two types of preferences. However, I have found no good reason to believe that our intuitions on deterministic objects are always more reliable than our intuitions on indeterministic objects ( Hansson 2001 ). To the contrary, we have in many contexts more experience from uncertain than from certain objects of value. It does not then seem reasonable to disregard all our intuitions on the former category from our deliberations, and reconstruct value assignments to them that are based only on our intuitions on the latter type of objects. Although not all combinations of deterministic and nondeterministic preferences are acceptable, a given set of deterministic preferences may be compatible with different (and mutually incompatible) sets of non-deterministic preferences.

In this perspective, the deductive reasoning of conventional decision theory should be replaced by consolidative reasoning ( 2001 ). Consolidation refers to the process of adjusting parts of a mental state in order to reduce its internal tensions. Consolidative reasoning may or may not lead to an end-point in the form of a reflective equilibrium. In real life, new tensions arise continuously in response to changes in the outer world, so that a reflective equilibrium may be as illusive as the end of the rainbow. Needless to say, this does not make the consolidative process less important.

In this perspective, moral philosophy and decision theory are not two distinct disciplines with separable subject matters, one of which should be treated prior to the other. Instead, the two disciplines have developed different approaches to one and the same problem—two approaches that stand in need for integration rather than separation. This is yet another major philosophical conclusion that seems to be unavoidable if we take issues of risk seriously—ethics and decision theory cannot any longer be kept apart.

The Causal Dilution Problem

Throughout the history of moral philosophy, moral theorizing has for the most part referred to a deterministic world in which the morally relevant properties of human actions are both well-determined and knowable. In recent years, moral philosophers have in most cases left it to decision theorists to analyze the complexities that the indeterminism of real life gives rise to. Mainstream ethical (and metaethical) theories still focus on deterministic problems; in fact they lack the means to deal with problems involving risk and uncertainty. As far as I can see, ethics still lives in a Newtonian world ( Hansson 2003 ).

How can we generalize ethical theories so that they can be effectively applied to problems involving risk and uncertainty? The problem of how to perform this generalization can be specified in terms of the causal dilution problem . ⁶

The causal dilution problem (general version) : Given the moral appraisals that a moral theory T makes of value-carriers with well-determined properties, what moral appraisals does (a generalized version of) T make of value-carriers whose properties are not well-determined beforehand?

The term "moral appraisal" covers a wide range of assignments of moral status, such as declarations that something is forbidden, permitted, morally required, good, bad, better than something else to which it is compared, etc. The term "value-carriers" refers to all entities that can be assigned (moral) value, including in particular human actions and the outcomes of human actions.

Under conditions of risk, we can restate the causal dilution problem as follows:

The causal dilution problem (probabilistic version) : Given the moral appraisals that a moral theory T makes of value-carriers with well-determined properties, what moral appraisals does (a generalized version of) T make of probabilistic mixtures of such value-carriers? How can major moral theories deal with the causal dilution problem?

Utilitarian Theories

There is an obvious but trivial answer to the causal dilution problem for utilitarianism ( Bergström 1996 , pp. 74-75). We can call it the "actualist" answer since it refers to what actually happens:

Actualism : The utility of a (probabilistic) mixture of potential outcomes is equal to the utility of the outcome that actually materializes.

To exemplify the actualist approach, consider an engineer's decision whether or not to reinforce a bridge before it is being used for a single, very heavy transport. There is a 50 % risk that the bridge will fall down if it is not reinforced. Suppose that she decides not to reinforce the bridge and that everything goes well; the bridge is not damaged. According to the actualist approach, what she did was right. This is, of course, contrary to common moral intuitions.

The actualist solution requires that we use moral terms such as "right" and "wrong" in a way that differs radically from ordinary usage. If we accept the actualist usage, then it will in most cases be impossible to know what is right or wrong (or permitted, morally required, good, best, etc.) to do. In this way, action-guidance is expelled from moral discourse. However, action-guidance is largely what we need ethics for. Therefore, this is an unusually unhelpful approach. If we follow it, then action-guidance will have to be reintroduced in some other way.

The standard decision-theoretical solution to the utilitarian causal dilution problem is the maximization of expected utility. To maximize expected utility means to choose among a set of alternatives one of those that have the highest expected, i.e. probability-weighted utility. Hence this decision rule is based on a precise method for dealing with probabilistic mixtures.

Expected utility : The utility of a probabilistic mixture of potential outcomes is equal to the probability-weighted average of the utilities of these outcomes.

The argument most commonly invoked in favor of maximizing objectivist expected utility is that this is a fairly safe method to maximize the outcome in the long run. Suppose, for instance, that the expected number of deaths in traffic accidents in a region will be 300 per year if safety belts are compulsory and 400 per year if they are optional. Then, if these calculations are correct, about 100 more persons per year will actually be killed in the latter case than in the former. We know, when choosing one of these options, whether it will lead to fewer or more deaths than the other option. If we aim at reducing the number of traffic casualties, then this can, due to the law of large numbers, safely be achieved by maximizing the expected utility (i.e., minimizing the expected number of deaths).

The validity of this argument depends on the large number of road accidents, that levels out random effects in the long run. Therefore, the argument is not valid for case-by-case decisions on unique or very rare events. Suppose, for instance, that we have a choice between a probability of .001 of an event that will kill 50 persons and the probability of .1 of an event that will kill one person. Here, random effects will not be leveled out as in the traffic belt case. In other words, we do not know, when choosing one of the options, whether or not it will lead to fewer deaths than the other option. In such a case, taken in isolation, there is no compelling reason to maximize expected utility.

Nevertheless, a decision in this case to prefer the first of the two options (with the lower number of expected deaths) may very well be based on a reasonable application of expected utility theory, namely if the decision is included in a sufficiently large group of decisions for which a metadecision has been made to maximize expected utility. As an example, a case can be made that a criterion for the regulation of safety equipment in motorcars should be one of maximizing expected utility (minimizing expected damage). The consistent application of this criterion in all the different specific regulatory decisions should minimize the damage caused by technical failures of motor vehicles.

The larger the group of decisions is that are covered by such a rule, the more efficient is the leveling-out effect. In other words, the larger the group of decisions, the larger catastrophic consequences can be leveled out. However, there is both a practical and an absolute limit to this effect. The practical limit is that decisions have to be made in manageable pieces. If too many issues are lumped together, then the problems of information processing may lead to losses that outweigh any gains that might have been hoped for. Obviously, decisions can be partitioned into manageable bundles in many different ways, and how this is done may have a strong influence on decision outcomes. As an example, the protection of workers against radiation may not be given the same priority if it is grouped together with other issues of radiation as if it is included among other issues of work environment.

The absolute limit to the leveling-out effect is that some extreme effects, such as a nuclear war or a major ecological threat to human life, cannot be leveled out even in the hypothetical limiting case in which all human decision-making aims at maximizing expected utility. Perhaps the best example of this is the Pentagon's use of secret utility assignments to accidental nuclear strike and to failure to respond to a nuclear attack, as a basis for the construction of command and control devices ( Paté-Cornell & Neu 1985 ).

Even in cases in which the leveling-out argument for expected utility maximization is valid, compliance with this principle is not required by rationality. In particular, it is quite possible for a rational agent to refrain from minimizing total damage in order to avoid imposing high-probability risks on individuals.

To see this, let us suppose that we have to choose, in an acute situation, between two ways to repair a serious gas leakage in the machine-room of a chemical factory. One of the options is to send in the repairman immediately. (There is only one person at hand who is competent to do the job.) He will then run a risk of .9 to die due to an explosion of the gas immediately after he has performed the necessary technical operations. The other option is to immediately let out gas into the environment. In that case, the repairman will run no particular risk, but each of 10 000 persons in the immediate vicinity of the plant runs a risk of .001 to be killed by the toxic effects of the gas. The maxim of maximizing expected utility requires that we send in the repairman to die. This is also a fairly safe way to minimize the number of actual deaths. However, it is not clear that it is the only possible response that is rational. A rational decision-maker may refrain from maximizing expected utility (minimizing expected damage) in order to avoid what would be unfair to a single individual and infringe her rights.

There is one further problem with expected utility maximization: Just like utilitarianism, it is strictly impersonal. Utilities and disutilities that pertain to different individuals are added, with no respect being paid to the fact that they are bound to different persons. ⁷ Indeed, just as in ordinary utilitarianism, persons have no role in the ethical calculus other than as bearers of utilities whose value is independent of whom they are carried by. Therefore, a disadvantage affecting one person can always be justified by a sufficiently large advantage to some other person. This feature of expected utility calculations can be clearly seen in risk analysis. In mainstream risk analysis, benefits for one person may easily outweigh risk-exposure affecting other persons. Consider a polluting industry somewhere in Sweden. The total economic advantages to the Swedish population of this industry outweigh the total health risks that the pollution gives rise to. However, for those who live in the neighborhood the situation is radically different. The whole health risk burden that the pollution from the plant gives rise to falls on them. Nevertheless, they receive a much smaller share of the economic advantages. In risk-benefit analysis, performed in the standard way as expected utility maximization, such distributional issues are disregarded. To the common moral intuition, this is an implausible way of thinking.

In summary, no plausible solution to the utilitarian causal dilution problem seems to be available.

Deontological and Rights-based Theories

Let us now turn to deontological and rights-based theories. The causal dilution problem for rights-based theories was formulated (in its probabilistic version) by Robert Nozick: "Imposing how slight a probability of a harm that violates someone's rights also violates his rights?" ( Nozick 1974 , p. 7; Cf. McKerlie 1986 ) In somewhat more general language we can restate it, and its deontological counterpart, as follows:

The causal dilution problem for deontological/rights-based moral theories (general version) : Given the duties/rights that a moral theory T assigns with respect to actions with well-determined properties, what duties/rights does (a generalized version of) T assign with respect to actions whose properties are not well-determined beforehand?

The causal dilution problem for deontological/rights-based moral theories (probabilistic version) : Given the duties/rights that a moral theory T assigns with respect to actions with well-determined properties, what duties/rights does (a generalized version of) T assign with respect to probabilistic mixtures of such actions?

An extension of a deontological theory to indeterministic cases can be obtained by just prescribing that a prohibition to bring about a certain outcome implies a prohibition to cause an increase in the risk of that outcome (even if the increase is very small). Similarly, for a rights-based theory, it could be claimed that if I have a right that you do not bring about a certain outcome, then I also have a right that you do not perform any action that has a non-zero risk of bringing about that outcome. Unfortunately, such a strict extension of rights and prohibitions is socially untenable. Your right not to be killed by me certainly implies a prohibition for me to perform certain acts that involve a risk of killing you, but it cannot prohibit all such acts. Such a strict interpretation would make human society impossible. I am allowed to drive a car in the town where you live, although this increases the risk of being killed by me (Cf. Fried 1978 , pp. 18-20; Kagan 1989 , p. 88).

Hence, rights and prohibitions have to be defeasible so that they can be cancelled when probabilities are small. The most obvious way to achieve this is to assign to each right (prohibition) a probability limit. Below that limit, the right (prohibition) is cancelled. However, as Nozick observed, such a solution is not credible since probability limits "cannot be utilized by a tradition which holds that stealing a penny or a pin or anything from someone violates his rights. That tradition does not select a threshold measure of harm as a lower limit, in the case of harms certain to occur" ( Nozick 1974 , p. 75)

Clearly, a moral theory need not treat a slight probability of a sizable harm in the same way that it treats a slight harm. The analogy is nevertheless relevant. The same basic property of traditional rights theories, namely the uncompromising way in which they protect against disadvantages for one person inflicted by another, prevents them from drawing a principled line either between harms or between probabilities in terms of their acceptability or negligibility. In particular, since no rights-based method for the determination of such probability limits seems to be available, they would have to be external to the rights-based theory. Exactly the same problem obtains for deontological theories.

Probability limits do not solve the causal dilution problem for these types of theories. As far as I am aware, no other solution of the causal dilution problem for these theories is available.

Contract Theories

Contract theories may perhaps appear somewhat more promising. The criterion that they offer for the deterministic case, namely consent among all those involved, can also be applied to risky options. Can we then solve the causal dilution problem for contract theories by saying that risk impositions should be accepted to the degree that they are supported by a consensus?

Unfortunately, this solution is far from unproblematic. Consent, as conceived in contract theories, is either actual or hypothetical. Actual consent does not seem to be a realistic criterion in a complex society in which everyone performs actions with marginal but additive effects on many people's lives. According to the criterion of actual consent, you have a veto against me or anyone else who wants to drive a car in the town where you live. Similarly, I have a veto against your use of coal to heat your house, since the emissions contribute to health risks that affect me. In this way we can all block each other, creating a society of stalemates. When all options in a decision are associated with risk, and all parties claim their rights to keep clear of the risks that others want to impose on them, the criterion of actual consent does not seem to be of much help.

We are left then with hypothetical consent. However, as the debate following Rawls's Theory of Justice has shown, there is no single decision-rule for risk and uncertainty that all participants in a hypothetical initial situation can be supposed to adhere to (See Hare 1973 ; Harsanyi 1975 ). It remains to show—if this can at all be done—that a viable consensus on risk-impositions can be reached among participants who apply different decision-rules in situations of risk and uncertainty. (If a unanimous decision is reached due to the fact that everybody applies the same decision-rule, then the problem has not been solved primarily by contract theory but by the underlying theory for individual decision-making.) As far as I can see, this has not been done, and hence, contract theory also does not have a solution to the causal dilution problem.

Figure 4. The standard view of how values of indeterministic options can be determined.

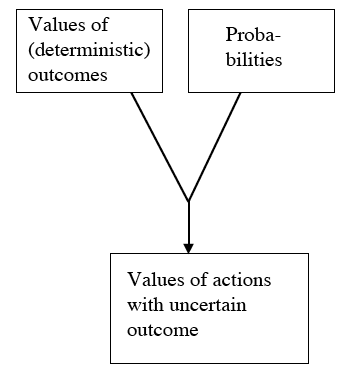
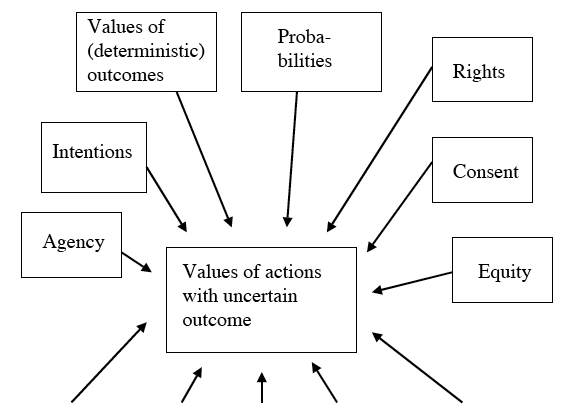
The difficulties that we encounter when trying to solve the causal dilution problem are indications of a deeper problem. In my view, the attempted solutions reviewed above are all based on an implicit derivation principle that is in fact quite implausible: It is assumed that given moral appraisals of actions with deterministic outcomes, we can derive moral appraisals of actions whose outcomes are probabilistic mixtures of such deterministic outcomes. In other words, it is assumed that probabilities and (deterministic) utilities are all the information that we need. ⁸ ( Figure 4 .)

Figure 5. A less incomplete picture of the influences on the values of indeterministic options.

In real life, there are always other factors in addition to probabilities and utilities that can—and should—influence a moral appraisal. The morally relevant aspects of situations of risk and uncertainty go far beyond the impersonal, free-floating sets of consequences that decision theory operates on. Risks are inextricably connected with interpersonal relationships. They do not just "exist"; they are taken, run, or imposed (Cf. Thomson 1985 ). To take just one example, it makes a moral difference if it is my own life or that of somebody else that I risk in order to earn a fortune for myself. Therefore, person-related aspects such as agency, intentionality, consent etc. will have to be taken seriously in any reasonably accurate account of real-life indeterminism. ( Figure 5 .)

A moral analysis of risk that includes considerations of agency and responsibility will be an analysis more in terms of the verb (to) "risk" than of the noun (a) "risk". ⁹ Major policy debates on risks have in part been clashes between the "noun" and the "verb" approach to risk. Proponents of nuclear energy emphasize how small the risks are, whereas opponents question the very act of risking improbable but potentially calamitous accidents.

We should therefore reformulate the causal dilution problem. I propose to replace it by an exemption problem that better reflects the moral issues of risk impositions:

The exemption problem : It is a prima facie moral right not to be exposed to risk of negative impact, such as damage to one's health or one's property, through the actions of others. What are the conditions under which this right is overridden ¹⁰ , so that someone is allowed to expose other persons to risk?

Attempts at a Solution

Let us now try an attack on the reformulated problem. A first, very simple, answer would be to refer to the weighing of risks and benefits.

(1)     Nobody should be exposed to a risk unless it is outweighed by a greater benefit.

This rule has the feature that we have seen above to be prominent in utilitarianism and in risk analysis: It allows us to expose one person to a risk in order to gain a benefit for someone else. We have already seen that this is implausible. What we need instead is a rule that respects the right of each individual not to be exploited by others who expose her to risks. Let us try going to the other extreme:

(2)     Nobody should be exposed to a risk unless it is outweighed by a greater benefit for herself.

This is very far-reaching, as we can see from our traffic example. It is of no use to me that people whom I do not know are allowed to drive a car in Stockholm, but their car-driving increases the risk that I will be the victim of a traffic accident or of diseases related to air pollution. They, on their side, have no use for me driving a car. Hence, rule (2) could be used to stop all car traffic—and indeed almost all technological activities. It would probably make human society impossible.

But we can modify the rule. In the spirit of social contract theory, we can introduce reciprocally beneficial rights. If you and everybody else are allowed to drive a car, exposing me to certain risks, then I am allowed to drive a car and expose you to the corresponding risks. This (we may suppose) is to the benefit of all of us. Generalizing the argument, we can modify the rule as follows;

(3)     Nobody should be exposed to a risk unless either (i) it is outweighed by a greater benefit for herself, or (ii) it is part of a system in which several persons are exposed to the same risk, and the benefits for her from this system outweigh the risk.

Rule 3 makes it possible to allow much of what rule 2 would prohibit, such as car-driving. But it is still a very limiting rule. It allows for agreements that several persons accept one and the same risk in order for all of them to obtain advantages from this risk-taking. It allows us to exchange apples for apples, but not apples for pears. Let us consider yet another example. In your neighborhood there is a factory that produces product A, which you do not use. The factory emits a chemical substance that gives rise to a very small risk to your health. At the same time, another factory, far away from your home, emits other chemicals in the production of product B that you use. One of the neighbors of this second factory does not use product B, but instead uses product A. In this way, and sometimes in much more complex chains, we may be said to exchange risks and benefits with each other. To justify this, we can introduce the following rule:

(4)     Nobody should be exposed to a risk unless it is part of a social system for risk-taking that works to her advantage.

Rule (4) allows everything that rule (3) allows, and more in addition to that. It has the important advantage of recognizing each person's individual rights (contrary to impersonal moral theories such as utilitarianism) but still making mutually beneficial adjustments possible (contrary to straight-forward applications of a theory of rights).

But rule (4) is not unproblematic. There is a remaining problem that can be seen from the following example: Suppose that the labor force in a society is divided into two classes. Members of the higher class lead a protected life, whereas members of the lower class are exposed to large occupational risks. For members of the higher class, this social system is highly advantageous. For members of the lower class, it is only marginally better than living outside of society. Rule (4) would not forbid this.

We therefore need to adjust the rule by including a clause of justice. We should acknowledge that the individual who is exposed to risks has a right to require, not only that the social system of risk should be to her advantage, but also that she receives a fair share of these advantages:

(5)     Nobody should be exposed to a risk unless it is part of an equitable social system for risk-taking that works to her advantage.

This is my preliminary proposal for a general criterion for the social acceptance of risks. It needs, of course, to be specified in several respects, both for theoretical purposes and to make it useful in concrete applications. Finally, let us compare this proposal to the dominating approach in risk analysis, that can be summarized as follows:

(RA)    A risk imposition is acceptable if the total benefits that it gives rise to outweigh the total risks, measured as the probability-weighted disutility of outcomes.

By choosing a rule such as (5), rather than (RA), we change the agenda for discussions on risk. We choose to treat each risk-exposed person as a sovereign individual who has a right to a fair treatment, rather than as a carrier of utilities and disutilities that would have the same worth if they were carried by someone else. We also choose another standard of proof. In order to argue, according to (RA) that it is acceptable to impose a risk on Ms. Smith, one has to give sufficient reasons for accepting the risk as such, as an impersonal entity. According to (5), one instead has to give sufficient reasons for accepting that Ms. Smith is exposed to the risk.

The lack of a qualified ethical analysis is probably one of the major reasons why so many mistakes have been made in the management of technological risks. As philosophers of technology, we can contribute to improving risk management and risk governance. At the same time, philosophy of risk provides us with new and theoretically important insights in areas as diverse as epistemology, philosophy of science, decision theory, and ethics. Both practically and theoretically, I believe this to be one of the most fruitful areas of study in present-day philosophy.

References

Bergström, L. "Reflections on consequentialism." Theoria 62 (1996): 74-94.

Fried, C. Right and Wrong . Harvard University Press, 1978.

Hansson, S.O. "The false promises of risk analysis." Ratio 6 (1993): 16-26.

________. "The Detection Level." Regulatory Toxicology and Pharmacology 22 (1995): 103- 109.

________. "Decision-Making Under Great Uncertainty." Philosophy of the Social Sciences 26 (1996): 369-386.

________. A Textbook of Belief Dynamics. Theory Change and Database Updating . Dordrecht: Kluwer, 1999a.

________. "The Moral Significance of Indetectable Effects." Risk 10 (1999b): 101-108.

________. "The Modes of Value." Philosophical Studies 104 (2001): 33-46.

________. "Replacing the No Effect Level (NOEL) with Bounded Effect Levels (OBEL and LEBEL)." Statistics in Medicine 21 (2002): 3071-3078.

Hansson, S.O. & Peterson, M. "Rights, Risks, and Residual Obligations." Risk Decision and Policy 6 (2001): 1-10.

________. "Ethical Criteria of Risk Acceptance." Erkenntnis 59 (2003): 291-309.

Hare, R.M. "Rawls's Theory of Justice." American Philosophical Quarterly 23 (1973): 144-155, 241-252.

Harsanyi, J.C. "Can the Maximin Principle Serve as a Basis for Morality - Critique of John Rawls theory." American Political Science Review 69 :2 (1975): 594-606.

Jeffrey, RC (1956) "Valuation and Acceptance of Scientific Hypotheses," Philosophy of Science 23 :237-249.

Kagan, S. The Limits of Morality . Oxford: Clarendon Press, 1989.

McKerlie, D. "Rights and Risk." Canadian Journal of Philosophy 16 (1986): 239-251.

McLaughlin, A. "Science, Reason and Value." Theory and Decision 1 (1970): 121-137.

Nozick, R. Anarchy, State, and Utopia . Basic Books, 1974.

Paté-Cornell, M.E. & Neu, J.E. "Warning Systems and Defense Policy: A Reliability Model for the Command and Control of U.S. Nuclear Forces." Risk Analysis 5 (1985): 121- 138.

Peirce, C (1934) "The Fixation of Belief." in Hartshorne, C. & Weiss, P. (eds.), Collected Papers of Charles Sanders Peirce , vol. 5. Cambridge: Harvard University Press. 1934, 223 - 247.

Thomson, J. "Imposing Risk." in Gibson, M. (ed.), To Breathe Freely . Totowa: Rowman & Allanheld. 1985, 124 - 140.

Trachtman, L.E. "Why Tolerate the Statistical Victim?" Hastings Center Report (February). 1985, p. 14.

Weale, A. "Statistical Lives and the Principle of Maximum Benefit." Journal of Medical Ethics 5 (1979): 185-195.

Notes

¹ The special case when all probabilities are either 0 or 1 coincides with decision-making under certainty.

² The case when they are not known at all is also called "decision-making under ignorance". On cases when not even the identity of the possible outcomes is known, see Hansson 1996 .

³ The word 'reduction' is used metaphorically. I do not wish to imply that all probability assignments or full beliefs have been preceded by more uncertainty-laden belief states, only that they can be seen as reductions in relation to an idealized belief state in which uncertainty is always fully recognized.

⁴ This is one of the reasons why belief revision models that represent belief states as sets of (sentences representing full) beliefs are an important complement to probabilistic models. Some features of doxastic behavior, notably features related to logic, are more realistically represented in the former type of models. See Hansson 1999a .

⁵ However, an argument can be made that refers to the special duties that we are assumed to have to certain people. I have, for instance, special duties to my children. My duty to come to their assistance is greater than my corresponding duties to my neighbour's children. Similarly, my duties towards the neighbour's children, with whom I am reasonably well acquainted, are stronger than those towards complete strangers. There is a special weight emanating from relationships between specific individuals. This special weight is not necessarily zero for people towards whom I have no other special relationship than that of being fellow human beings. To the contrary, it would seem natural to assume that it is still above zero for them, and zero only for persons who have not even been identified. It can then be argued that the trapped miners stand in the same type of relationship to the statistical beneficiaries of preventive medicine as my kin and friends to the trapped miners. - In many cases, the morally relevant special relations between identified persons can be expressed in terms of rights. The trapped miners may be said to have a right to our assistance, whereas in the case of the statistical victims there are no identifiable rights-holders and hence no rights.

⁶ There is also another form of causal dilution, that arises when one's action is one of several contributing causes of an outcome. The present paper deals only with such causal dilution that is due to uncertainty of the effects of actions.

⁷ The addition of utilities and disutilities pertaining to one and the same person is not either unproblematic, but that issue will not be discussed here.

⁸ The maximin rule goes one step further, i.e. it dismisses probabilities and makes use only of (deterministic) utilities.

⁹ The notion of risking is in need of clarification. In order to risk something, must I increase its probability, or causally contribute to it? Can I be said to risk an outcome that I have no means of knowing that I contribute to? The discussion of these definitional issues will have to be deferred to another occasion.

¹⁰ We should require only that the right be overridden, not that it be cancelled altogether (See Hansson & Peterson 2001 ).