SPT v9n2 - A Model-based Approach to Technological Theories

A Model-based Approach to Technological Theories

Ana Cuevas-Badallo
acuevas@usal.es
Lecturer at the Philosophy Department.
University of Salamanca (Spain)

Abstract

Several authors have studied and pointed out the main characteristics of engineering sciences. This paper deals with the analysis of one of these sciences, strength of materials, and shows how the practical goal of this science may have epistemological consequences. For this purpose, the model-based explanation of scientific theories proposed by Ronald Giere, especially his “similarity” relationship, is also discussed. Regarding engineering sciences, it is remarkable how important practical purposes are when developing and consolidating theories. The last section is related with the possible different reasons for building a set of models from the engineering point of view. ¹

1. Introduction

Philosophers of technology – those who deal with the consequences of technological developments as well as those who have proposed an analytical characterization – agree on pointing out that there is a close relationship between technology and science. In quite recent works, ² some of them show us that while it is true that technology depends on science to develop the basic knowledge required for innovation, it is also true that contemporary science would be impossible without technological artifacts used in observation, experimentation, and the designing of models. Therefore, the definition of technology as an applied science widespread among certain groups of philosophers of science in the second third of the last century is now considered a useless simplification created in order to understand the complex nature of technology.

Some historians, like Edwin Layton; economists, like Nathan Rosenberg ( Rosenberg 1982 ), Richard P. Nelson ( Nelson 1982 ) and Christopher Freeman ( Freeman 1982 ); engineers, like Walter Vincenti; and philosophers, like Joseph Agassi, Friedrich Rapp, and Ilkaa Niiniluoto, went even further and pointed out that sometimes technological developments may require new technological-scientific knowledge: the so-called engineering or technological theories.

The first research about technological knowledge dealt almost exclusively with operational knowledge or know-how. This operational knowledge was often subjective in nature, different from all good theoretical knowledge ( Drucker 1961 , 1963 ; Hall 1962 ; Feibleman 1966 ). Some philosophers appropriately claimed that know-how is not the only kind of proper technological knowledge: they had forgotten the kind of knowledge required in designing complex artifacts. Know-how alone – at least the kind of knowhow that a craftsman should have – is not sufficient. This seemed a good reason to start defining know-how of a high level, and highly sophisticated operational knowledge, no longer beyond words but still without the degree of elaboration of any scientific theory ( Bucciarelli 1988 , 1994 ; Vincenti 1990 , 207-225; Petroski 1992 , 1996 ; Constant 1999 ). At the present time there is another line of research dealing with the knowledge that emerged during the manufacturing process of artifacts ( Baird 2000 , 2001a , 2001b , 2002 ). All these studies have been very interesting and relevant in gaining a better understanding of technological knowledge. However, is there not any other task for the epistemology of technology? I assume there are two different answers to this question, each of them leading to equally different attitudes. Those who maintain that the only theoretical knowledge involved in technology comes from developments in natural, formal or social sciences would have to agree that the kinds of studies mentioned above are all that we can expect regarding the “epistemology” of technology. On the other hand, as some authors think plausible, if one admits certain technological-scientific theories as one of the elements of modern technology, then there is a field for epistemological inquiry concerning particular features of this kind of knowledge; methodology involved in these researches; characteristics of the outcomes; roles of theories, laws, and hypotheses in the process of developing knowledge, and in the process of designing and manufacturing technological artifacts; and, finally, the relationships between these technological theories and the scientific ones.

This paper attempts to show an epistemological revision of one of these theories, strength of materials, and describe it as a scientific theory in a similar sense as Ronald Giere has proposed. ³ Strength of materials fits quite well with Giere’s description of scientific theories, but it has stronger practical applications and a clear epistemological significance.

2. Precedents

More than a few authors, among whom are Mario ( Bunge 1966 , 1967 ), Edwin Layton ( 1971, 1974 , 1976 , 1979 , 1987 ), Ladislav Tondl ( 1973 ), Joseph Agassi ( 1980 , 1985 ), Fredrich Rapp ( 1981 ), Walter Vincenti ( 1990 , 2001 ), and Ilkaa Niiniluoto ( 1995 ), ⁴ suggested that technologists themselves are able to develop theoretical knowledge. All of these authors distinguished a group of sciences not included in the more habitual classifications, and agreed these special sciences share many features. As sciences, they require experimental research and mathematical language (Rapp); they deal with the same laws of nature as the rest of sciences (Bunge, Rapp, and Vincenti); they are both descriptive (Rapp and Niiniluoto) and predictive (Rapp and Bunge); their outcomes are shared and taught in similar ways of communication and training as the other sciences have been (Layton and Vincenti); they are a result of the division of labor (Tondl, Layton, and Vincenti); and the development of their knowledge is cumulative (Layton and Vincenti ⁵ ). In spite of many discrepancies among these authors, all of them agreed on this: the practical goal that directs these sciences is what makes them different from the other sciences. Engineering scientists work with the aim of designing and producing artifacts, while other scientists build up their theories so as to get a better comprehension of observable phenomena.

These contributions made it possible to question the simplistic idea that all theoretical knowledge comes from natural sciences and then is applied to technology. Obviously this idea is still widely accepted. For instance, in the cases of Bunge and Rapp, there still remains the tendency to consider this knowledge the result of certain processes of transformation (never adequately explained) of previous knowledge developed by natural scientists. This tendency is derived from the privileged relationship some philosophers consider to exist between scientific knowledge and reality: scientific theories provide accurate knowledge about the world (realism), and the artifacts created based on that knowledge supposedly validates this thesis. ⁶

This idea is just partially correct. First, it is not plausible that all natural scientific theories may be applied in order to design a technological device (this is a widespread opinion and does not deserve more attention). Secondly, in order to explain the highly sophisticated knowledge involved in designing and manufacturing technological artifacts, certain scientific theories are necessary. However, in many cases, current scientific theories cannot adequately solve every problem emerging during technological processes, and technologists themselves must face up to the task of developing their own theoretical knowledge. Artifacts manufactured through such a process work effectively, though with limitations. The fact that these artifacts validate use of technological knowledge implies a non-naïve realism.

Recent developments in theory of science show different possibilities with the aim of defending this non-naïve realism that does not have the same defects of the former realisms. It is the case with Ronald Giere and his realist constructive perspective: ⁷ his perspective is realist, because from the ontological point of view, he considers that the world exists independently of our knowledge. Likewise, from the epistemological point of view, he does not accept skepticism and assumes that it is possible to know entities in the world, though in a different way than that in which a realism without restrictions would maintain Giere 1988 , 95). Giere’s view is commonly framed in the so-called “semantic view of theories,” in which other well known philosophers such as Patrick Suppes, Frederick Suppe, ⁸ and Bas van Fraassen have made important contributions. The semantic view was conceived as an alternative to the “syntactic approach” of the received view. Instead of sets of true propositions about the world, theories are now better understood as sets or clusters of models. It is generally considered that the relationship between models and the world must be an isomorphic one. Nevertheless, Giere considers it more accurate to say that the relations between models and the world are similarity relationships . There are no true theories, only catalogues of cases in which models “fit” well enough with systems of the world. ⁹ These models are generated by scientists using general principles and specific conditions ( Giere 2002 , 5). General principles – which in other perspectives are scientific laws – are not universal truths, but, at best, truths consensually agreed upon by scientists for a specific model or cluster of models. ¹⁰ The degree of similarity will depend on pragmatic issues and not just on ontological and epistemological ones. The basis for choosing between different similar models is one of the more controversial aspects of Giere’s perspective. A new possibility for engineering sciences will be introduced in sections 4.3 and 4.4, where different values and their importance in strength of materials are suggested.

Another interesting feature of Giere’s realism is the incorporation of some constructivist elements generally considered contrary to traditional realism. He maintains that science is made by human beings. This is certainly an obvious characteristic, but it is also frequently forgotten. Scientists, as intentional agents, use models in order to represent some aspects of the world with determined purposes. From the very beginning, some values are involved in the choice of the best model, the most important being to prefer a model that provides the most accurate potential representation. The scientific community will help to reach a consensus regarding validity of motives. ¹¹ Nevertheless Giere’s approach does not imply any relativism from the ontological point of view. Scientists choose those aspects of phenomena they are going to deal with, that is to say, the properties they consider relevant to their purposes, while ignoring others. ¹² This is not to say that scientists “invent” reality, the position which a more radical constructivist would defend, but rather that the world is complex enough so as to admit different models about the same phenomena without necessarily implying that only one of them is correct. ¹³ It all depends on the purposes for which the models are devised.

However, in the case of the engineering sciences, Giere’s constructive realism may be interpreted as having instrumentalist characteristics. This claim could be controversial, because some philosophers tend to think of instrumentalism as a kind of relativism not compatible with realism. However, this is not the case, al least, for engineering sciences. When something works in the world effectively it is not a relative matter, nor is it simply to prefer the most adequate model for achieving that goal. On the other hand, to maintain an instrumentalist position regarding the engineering sciences does not necessarily mean that this philosophical interpretation of the nature of scientific theories is appropriate for other kind of sciences. The reason why the scientific community prefers – temporarily – one model instead of others is not necessarily to choose the model that allows them to build the most efficient artifact. Nevertheless, this could be the most important reason for scientific-technologist communities to consider this model.

The time has come to introduce strength of materials as a theory with both practical and epistemological value. If it is possible to show that this engineering theory can be considered as a cluster of models based on general principles and specific conditions, that these models represent some aspects of the world, and that they have been generated and are effective in accomplishing specific purposes, then there is no good reason to separate this science from other scientific disciplines. ¹⁴ Of course, strength of materials has special features derived from its different pragmatic status: practical goals have epistemological effects on theories. Nevertheless, the fundamental structure of this technological science is no different from the structure of other scientific theories. Let’s now take a look at the shape of the models, the principles on which these models are based, the specific conditions that the models refer to, and the purposes that direct strength of materials.

3. Strength of Materials in textbooks.

Textbooks are the standard form for displaying scientific theories, as well as the key tool for transmitting knowledge in our society ( Giere 1988 , 63; and Giere 1999a , 50). Theories appear in these books in their most developed and corroborated version. Although textbooks – as Kuhn accurately pointed out ( Kuhn 1970 , 137-138) – may be neither the source for the historical reconstruction of the sciences, nor the most up-to-date versions, those books can accurately describe theories from the scientists’ point of view. This section analyzes some noteworthy handbooks on strength of materials from different times: the works of Stephen Timoshenko ( 1930 , 1935 , 1953 ), considered the founder of modern strength of materials; P. A. Stepin ( 1963 ); A. A. Ilyushin and V. S. Lensky ( 1967 ); Ivan Feodosiev ( 1968 ); Bela I. Sandor ( 1978 ); G. S. Pisarenko, A. P. Yakovlel, and V. V. Matveev (1979); and, Nicholas Willems, John T. Easley, and Stanley T. Rolfe ( 1981 ). ¹⁵

( Giere 1988 ) presents the example of the pendulum in theoretical mechanics and analyzes all the models and simplifications used in the textbooks related to it. In this paper, instead of doing something similar, choosing a single structural element among the formulas of the strength of materials, the whole theory will be considered. The reason for doing that is because strength of materials is not as well known as the mechanics. I realize the difficulty of showing all the features of a complex theory within the length of this paper. Nevertheless, the purpose of this article is to open the possibility of understanding engineering sciences from a modelistic point of view. Future work will be done in order to analyze the particular structural elements.

3.1. Definition, justification, and subject matter.

All these textbooks start with a definition of the discipline, offered immediately after a justification of the field because of its usefulness for designing effective artifacts. Usually, the books propose that strength of materials studies the relationships between external loads applied to a body and the effects of the loads on the internal structure of that body. It is worth noting that all these texts propose that, with the knowledge provided by strength of materials, it is feasible to calculate the necessary and safe dimensions of different parts of structures or pieces of machines.

Following the definition and justification, the three main issues the theory deals with are distinguished: first, a study about internal stresses presented in materials; secondly, studies in order to determine different plastic and elastic deformations that bodies- such as elements of structures and components of machines- can undergo under the action of external forces or loads (in terms of the theory); thirdly, the theory deals with the main concepts of strength of materials: stability, fatigue, and failure of components in some structures. The aim of strength of materials is to build the knowledge necessary for constructing artifacts that can effectively sustain the conditions they are going to be subjected to during their life.

3.2. Idealizations and simplifications.

Once the definition and the usefulness of the theory have been settled, and different properties of the bodies have been explained, the textbooks propose an explanation of the idealizations and simplifications that the theory assumes. The authors explicitly show the specific characteristics of materials that are relevant for the theory, while ignoring those properties irrelevant to the engineers’ purposes. The authors know (and they explicitly say so) that on many occasions the characteristics they consider relevant may contradict conclusions reached by other scientific theories, ¹⁶ though the engineers accept these special features for the sake of applicability.

(I) First, the properties of materials are idealized. Thus, materials are considered as homogeneous and continuous , despite the internal properties of different materials. ¹⁷ The concept of continuity is derived from the concept of homogeneity, due to the fact that matter totally occupies a solid’s volume. The assumption of the homogeneity property allows the applications of infinitesimal calculus to solids. Moreover, materials are usually considered isotropic, that is, the properties in any part of the material are independent of the original angular orientation. ¹⁸

(II) Secondly, the shapes of materials are simplified. The geometrical shapes of solids are reduced in strength of materials to four elemental forms: beams, plates, vaults, and solids. ¹⁹ Generally the textbooks provide illustrations of these forms together with some applications as parts of structures or of machines.

(III) Thirdly, the systems of force applied on different elements of structures are idealized. The study on these forces and the deformations generated by them are, properly speaking, the theory’s core. From a more general point of view, the textbooks distinguish between external and internal forces . The first third of the textbooks is usually dedicated to the study of internal strains and the second part to the analysis of external forces or loads.

3.3. Strains and deformations.

Internal strains are determined by the interaction between parts of the body, within well established limits. It should be noted that internal forces work between particles contiguous within the body affected by the load. Indeed, that property is essential to define the solid’s limits, since forces that are external to a system may be internal in another, and vice versa. With the aim of determining these internal forces, the authors apply the method of cross-sections . The method consists of getting a beam mentally cross-sectioned into two parts. “Internal forces determine the interaction between the particles of a body on the different sides of the section passed through the body” ( Feodosiev 1968 , 20). According to the action and reaction principle, internal forces are always reciprocal. ²⁰ (Figure 1.)

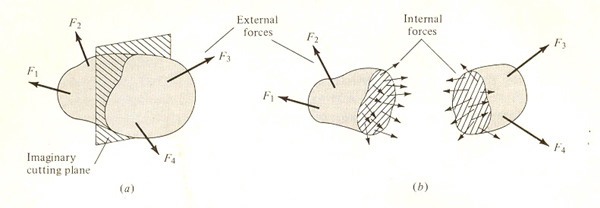
The concept of stress is used to characterize the law of distribution of internal forces in a cross-section, since stress will be the measure of intensity of internal forces. The total amount of stress in a point of the cross-section is a vectorial magnitude, being analyzed in three components: one normal stress and two tangential stresses . An accurate calculus of stress is essential to decide whether or not a given structure fulfills the safety conditions. Therefore, engineers need to know the purpose of the structure before doing any calculation. ²¹

Following the discussion, authors then show how the ideas of strain and deformation can be used to construct effective artifacts. The authors usually present these examples side by side with graphic representations, as well as the corresponding mathematical calculi.

The textbooks discuss the relationship between strain and deformation, and clarify the fundamental difference between strength of materials and other theories, such as Newtonian mechanics (statics and dynamics). Physicists postulate that all bodies are perfectly rigid; they assume that the shape of bodies does not change under external loads. Nevertheless, as a matter of fact, all the shapes of material bodies change when they are subjected to external loads, though to a different degree. Despite the fact that those changes can be small, they are very significant, and must be acknowledged in order to build safe constructions. These changes are referred to as deformations, and involve the action of strains. Engineers define normal strain as changes in the length of bodies under the effect of a load. The calculations are proposed to avoid the physical breakdown of the material under strain. The textbooks include diagrams that show the different relationships between strain and deformation of different materials.

Since stress is proportional to load and strain is proportional to deformation, it implies that stress is proportional to strain. The next formula expresses the ratio between strain and stress:

σ = E ε

E means the proportionality coefficient (a physical constant of the material, experimentally obtained and measured in kg/cm ² ). It is also called the elasticity module or Young’s module. s is the normal stress, and e is the normal strain. This formula is also known as Hooke’s law, ²² and engineers consider it to be an approximate law, since “for certain materials, such as steel, it [Hooke’s law] holds with a high degree of accuracy over a wide range of stress. In some cases, however, noticeable deviations from Hooke’s law are observed” ( Feodosiev 1968 , 37). In those cases where the principle is not applicable, engineers calculate deformations with a function (obtained from experimentation on the material) that describes the curve of the specific material.

The different textbooks reveal that the behavioral relationship between strain and deformation of a great number of materials varies because of different rates of load and temperature. Therefore, engineers do different experiments in order to know the exact rates for each material. Hooke’s principle is generalized and shown as a set of basic equations. These equations are applicable to different structures with the aim of calculating stresses in a linear-elastic area. The books also describe many instances in which Hooke’s law is applied to different materials and structures, and show how the law varies depending on conditions, materials, and structures. So far the considerations have been about strain and deformation. The next sections discuss the analysis of different kinds of external loads.

3.4. Analysis of loads.

External forces or loads are divided into six different kinds: (i) body forces, (ii) surface forces, (iii) concentrated loads, (iv) distributed loads, (v) static loads, and (vi) dynamic loads. All these different loads are distinguished with the aim of simplifying the complex external loads acting on a structure. Body forces (for example, weight and magnetic forces), are considered to be distributed in the solid’s volume, and applied to every particle of the body. Surface forces refer to specific areas of the surface, and are established at the point of contact between objects. Concentrated loads are concentrated in specific parts of the bodies. Distributed loads are distributed along the length, the surface, or the volume. Both concentrated and distributed loads may be considered static or dynamic . Static loads are applied to structures in an extremely gradual manner, “increasing from zero to their final value, and then either do not change their magnitude, direction or point of application with time at all or change them very slightly, so that accelerations occurring in this case can be neglected” ( Stepin 1963 , 17). Loads are dynamic when they “vary in time with great speed (for example, impact loads of short duration)” ( Stepin 1963 , 17). The authors take into account the case of periodically repeated loads : those cases in which the change of loads is periodically repeated and in which maximum levels of loads are continuously repeated after a period of time.

Once the general characterization about loads is proposed, the textbooks distinguish between different kinds of loads: torsion, tension, and deflection. Hooke’s law, as well as Saint-Venant’s principle, is used in the explanation of these loads. According to Saint-Venant’s principle, “At points of a body which are sufficiently distant from the places of application of loads, internal forces depend to a very small extent, on the particular manner in which these loads are applied” ( Stepin 1963 , 15). These principles are applied for the sake of simplifying the schemes of calculus. In other words, engineers realize that material properties are fundamentally more complex, but calculi obtained using these assumptions provide a range of outcomes more useful for their purposes. These three kinds of loads are discussed at great length in strength of materials textbooks.

Torsion is analyzed thus: “a bar (shaft) undergoes torsion, if at its cross sections twisting moment occurs, i.e. moments lying in the plane of the section. The internal twisting moments are generally produced by external moments.” ²³ At this point, the authors usually assume some properties about materials to support theoretical simplification. The simplest case of torsion, the torsion of a beam, is submitted, along with the formulas needed to calculate the deformation made by loads. Some examples are included in which different materials are subjected to dynamic and static torsions, and average values of the action of the loads are shown. Pictures of concrete models accompany the examples.

Tension is also considered. Again, using the example of a beam, tension is defined as occurring when “some forces are applied all along the beam’s axis but in opposite directions. In that case there is a displacement of advance in the cross-sections all along the beam’s axis.” ²⁴ The authors propose formulas for possible idealized forms with both static and dynamic loads. Once more, numerous illustrative examples are offered. The authors incorporate beams and bolts in their experiments to show how different materials behave regarding their shapes and sizes. These sizes are offered between minimum and maximum rates.

Deflection “entails the deviation of a straight beam’s axis or the change of curvature of a curved beam.” ²⁵ The textbooks present some methods to determine deflection of beams, along with several examples of elastic and plastic materials, as well as beams composed of two materials. In many textbooks, authors offer tables where kinds of loads, maximum moment, deviation equation (that is, the deformation), and maximum deviation appear related.

Once different loads have been explained, the authors consider cases in which these different loads are combined. The principle of superposition (principle of independence of action and addition of forces) is assumed to be applicable for the solution of most strength of materials problems. The textbooks show some methods for calculation, the most common being the circle of Mohr: a method that allows engineers to calculate the strain in different points of a material subjected to combined loads. The textbooks are again riddled with numerous practical examples applying this method. All those models where different kinds of loads are analyzed and divided will be used by designers in order to build efficient and safe artifacts, being able to derive values for the different internal loads and stresses in a varied range of materials.

3.5. Failures, fatigue, and application in building.

The last third of the textbooks deals with practical applications of strength of materials to specific designs. The concepts of fatigue and fracture are also explained. Certain structures are technically acceptable if they fulfill all safety requirements. Given these considerations, strength of materials textbooks provide formulas to determine security factors of structures.

One of the main reasons materials fail is instability under a load. This lack of stability may be due to several causes: the support upon which the material rests might be insufficient, or calculation may underestimate the materials’ thickness. The problem of failure is one of the main concerns of every engineer. ²⁶ That is the reason that they study the critical load (the minimum load at which instability occurs) and the critical strain (the strain which goes with instability) concerning different forms (such as columns, beams, and sheets), and diverse materials (steel, reinforced steel, and cement, for instance).

Failures and discontinuities within materials themselves may contribute to instability. In ideal cases, materials are continuous, but in actual structures and machines, engineers need to make orifices, cuts, and gratings in order to have different parts joined. Engineers need to know how these modifications, as well as the actual conditions (such as temperature, or load magnitude), could affect the calculus of distributed strain on materials. The textbooks offer some possible cases applied to different materials, along with tables and the most common methods for calculating the ratio between discontinuities, forms, and typical loads materials are going to deal with (again with many examples).

Fatigue is the last analyzed problem. Fatigue usually appears when materials are subjected to repeated loads in many cycles. This is the main criterion engineers ought to take into account in order to warrant safety and reliability of machines or structures. The authors of strength of materials textbooks usually distinguish between short cycle fatigue, in which the number of loads is relatively small (fewer than 10 ⁴ ); and long cycle fatigue, in which the number of loads is larger than 10 ⁴ . The behavior of the different structures under fatigue must be “modeled” ²⁷ as accurately as possible through experiments in the laboratory. The most general types of experiments to test and measure materials’ resistance to fatigue are: (i) laboratory short scale tests, in which engineers get information about the behavior of idealized forms of materials, and (ii) direct tests on actual components of machines or structures. The books offer instances of both types of experiments and different outcomes carried out with different materials.

Besides the systematic presentation of strength of materials, most of the textbooks include tables ²⁸ that deal with: (i) standard physical properties (such as elasticity module, final resistance, and lineal expansion coefficient on the basis of the temperature) of regular materials (such as different types of steel, iron, brass, copper, aluminum, wood, titanium, and cement); (ii) properties of the wide flange sections properties, standard I-beam sections, equal and unequal angle sections; (iii) elastic curves for different kinds of beams; (iv) and torsion constants of several structures.

4. Epistemological summing-up.

So far the main issues strength of materials deals with have been shown. ²⁹ It is time to interpret these characteristics in epistemological terms. The next paragraphs analyze this theory as a set or cluster of models with representational goals.

4.1. Definition of the subject matter.

The first thing the authors establish in the textbooks is to define those aspects of the world that strength of materials deals with. They state that strength of materials is used primarily for technological purposes. The texts focus on the relationships between loads or external forces and deformations of materials. It is necessary to idealize ³⁰ some properties of real systems: materials are considered to be homogeneous, continuous, and isotropic, despite the fact that these properties are not accepted in other well consolidated scientific models. For the purpose of strength of materials, “these particularities are not very important, since strength of materials deals with the study of structures of which dimensions are much superior, not only to those of atoms, but to those of crystals also” ( Feodosiev 1968 , 14).

According to the traditional view of scientific theories, it is possible to maintain that these assumptions are false, since in more consolidated theories (such as physics), matter is assumed to have quite different properties (matter is neither homogeneous nor continuous, and is isotropic in just some cases). In contrast, from the perspective of the model-based and representational view of theories, it is possible to say that strength of materials proposes representational models about some systems of the world, and that systems can be considered to have the properties of homogeneity, continuity, and isomorphism. That is to say, different purposes can bring about the generation of different models. Margaret Morrison ( Morrison 1999 ) and Paul Teller ( Teller 2001 ) have studied the case of water: how water can be considered to be either a collection of molecules (when the diffusion of a drop of ink in a glass of water is analyzed); or a fluid (to analyze the behavior of water circulating in pipes). In other words, there can be multiple models dealing with the same phenomena, if those models deal with different properties of phenomena, and the purposes for analyzing are also different. Reality is too complex to be grasped with only one theory. Theories are sets of models that search for characterizations or explanations of the behavior of some systems that are nothing but partial aspects of reality. In this sense, strength of materials is doing nothing different. The only difference has to do with the purposes of the research. ³¹ The following sections discuss this issue in greater detail.

4.2. Types of models utilized.

As Giere has pointed out ( 1999b ), it is possible to distinguish between different types of representational models: (i) material models , among which he includes maps, diagrams, and scale models; (ii) abstract models , such as pure mathematical models, applied mathematical models, and theoretical models built with theoretical principles (such as Newton’s laws, Schroedinger’s equation for quantum mechanics, Darwin’s theory of natural selection, and Mendel’s laws of genetics). All these models can be used to build scientific theories, including strength of materials, as is shown next.

In the case of strength of materials, the authors abstract basic forms of materials. ³² Basic forms are presented using graphic models of machines and structures. The structures can be separated into parts that fit one of the four basic forms of the theory. The graphic models are limited and can only be considered to represent those characteristics of real objects that permit engineers to design workable artifacts. The models should not be assumed to also represent characteristics of real objects. The models are context dependent ( Giere 1999b , 4).

The central aspects of the theory deal with two idealized aspects of forces, being understood as strains, or internal forces, and loads, or external forces. Authors use plane cross-sections, graphic idealized models of how forces work, to illustrate the differences between the various internal forces. Plane cross sections are found in every textbook and are quite helpful for understanding the mathematical model provided to account for different strains. Numerous examples are used to illustrate this general model.

The core of strength of materials deals with the relationship between strain, stress, and deformation. Pure mathematical models about the forces show the relationship between strain and stress and deformation of bodies. Hooke’s law defines the relationships between strain, stress and deformation. First, the law is explained in simple mathematical form, and afterwards as a generalized set of fundamental equations (sets of mathematical models). Hooke’s law behaves as a general principle , that is, it is used to build models about different loads and deformations of materials and structures. The authors of all of the textbooks show how the law behaves with standard materials using many examples.

The next chapters deal with the construction of models using Hooke’s law, taking into account different loads relevant to engineers’ purposes. Textbooks analyze idealized or pure forms of the application of loads, which are torsion, tension, and deflection. It is important to distinguish between dynamic or static loads because these different loads lead to different pure mathematical models . It is also relevant if dynamic loads are continuously repeated, because this can cause fatigue of materials that lead to breaks. All these models are built upon Hooke’s law, and have a great number of practical design applications.

Since loads do not usually act alone, but in conjunction with different forces inherent to structures and machines, textbooks propose main models to account for different combinatory possibilities. In terms of the theory’s purposes, these models are still excessively idealized . Strength of materials has to facilitate the construction of real designs, and these designs have to fulfill some verification and safety criteria. Engineers must be cautious, because materials are not perfectly homogeneous, are affected by fatigue, and are degradable. The last parts of these books are devoted to analyzing the real conditions and environmental pressures, in which materials and structures must work. Taking these real conditions into account, the authors of the textbooks propose – from abstract mathematical models – applied mathematical models , with more detailed factors of correction.

Presentations of strength of materials in the different textbooks incorporate all of Giere’s models. The main principle of strength of materials, Hooke’s law, is the basis for many of the models. At the same time, it is possible to point out an important difference between Giere’s characterization of the natural sciences and the engineering theory analyzed in this paper: strength of materials calls for applied mathematical models rather than the more abstract models found in natural scientific theories. This is the first point at which strength of materials significantly diverges from other scientific theories. ³³ Mathematical models are usually presented in their pure form and rarely with correction factors. Strength of materials is directed toward the construction of safe and effective artifacts. This practical purpose turns out to be a factor of the greatest importance in order to establish the extent of similarity between models and systems of the world.

4.3. Similarity between models and the world.

The concept of similarity is one of the most controversial of Giere’s proposals. On the one hand, some critics have pointed out that it is necessary to show how one model, which is an abstract phenomenon, can be “similar” to a particular object in the world. Teller ( 2001 , 399) gives an answer to this question: similarity does not take place between different ontological categories, but between properties of models and properties of specific systems.

There is still another problem related to the reasons why scientists prefer a specific model. According to Giere, scientists, generally speaking, prefer models that represent those aspects of reality in the most accurate way that they consider relevant to their purposes. Scientists select the appropriate model through experiment ( Giere 1999a , 53). Nevertheless, somebody could argue that this is not a convincing criterion from which to establish the extent of similarity between one model and one system in the world. The phenomena that scientists usually handle in experiments do not naturally occur, but these facts are artificially produced and confined to special conditions in the laboratory. Even so, experiments can be reproduced in a controlled manner by different scientists in different laboratories, without any modification of the results. ³⁴

Giere maintains that scientists do not make decisions as if they were Bayesian agents, nor do they behave as “satisficers,” as Herbert Simon holds ( 1945 ). If scientists are rational agents, then it is necessary to admit that scientists pursue the achievement of some goals. Thus, the more efficient a scientist’s method, the more rational it can be considered ( Giere 1988 , 160; also 1999a, 82). In other words, scientists’ rationality is “conditional” or “instrumental,” since scientists behave rationally when propounding the model that better fits with reality. ³⁵

4.4. Reasons for choosing one model in strength of materials.

For sake of the argument, let’s agree that strength of materials could be characterized in terms of a cluster of different kinds of models. It could be interesting to determine if there are some differences between the goals pursued by basic scientists and engineering-scientists when they are building their respective models. In the case of strength of materials, the main desired objective of engineers developing the theory is to put forward theoretical and mathematical models which can be useful in order to design safe, lasting and efficient artifacts. In the case of “basic” sciences, the main goal is to know how things are, that is, suggest models that represent and explain accurately some interesting aspects of reality. Those different goals will determine differences in the attributes considered valuable in both cases. As Ernan McMullin has pointed out:

A property or a set of properties may count as a value in an entity of a particular kind because it is desirable for an entity of that kind. (The same property in a different entity might not count as a value.) […]The desirable property is an objective characteristic of the entity. We can thus call it a characteristic value. In some cases, it is relative to a pattern of human ends; in others, it is not. In some cases, a characteristic value is a means to an end served by the entity possessing it; in others, it is not. In all cases, it serves to make its possessor function better as an entity of that kind” ( McMullin 1982 , 5).

During the last decades, some philosophers have been trying to put forward a list of desirable attributes by different sciences. ³⁶ So far, there has not been agreement on a particular set of principles, and other problems arise. First, as Kuhn pointed out ( 1977 , 331), different scientists may evaluate differently the attributes of a particular theory. There is no algorithm for an assessment of this kind, so it will depend on the individual scientist’s training, experience, and goals. Second, “scientists may not attach the same relative weights to different characteristic values of theory; that is, they may not value the characteristics in the same way, when, for example, consistency is to be weighed over against predictive accuracy. It is above all because theory has more than one criterion to satisfy, and because the ‘valuings’ given these criteria by different scientists may greatly differ, that disagreement in regard to the merits of rival theories can on occasion be so intractable” ( McMullin 1982 , 16). One theory, hypothesis, or model can be empirically adequate but not very simple, or can be simple but not very explanatory, and so on… which is why scientists need to weigh up these attributes and determine which model is the best one among different possibilities.

In order to do that, scientists could behave as Bayesian maximizers, or as Simon’s satisficers. Nevertheless, both of these alternatives have some problems, as Giere has pointed out ( Giere 1988 , 145-165; see also Giere 1969 against the application of game theory to decisions related to hypotheses). Alex Michalos (1970) suggested another solution that can be more realistic than the other ones. Michalos’ proposal evaluates the costs and benefits of choosing a hypothesis (or a model in our terms), and takes into account the different desirable characteristics that scientists can expect in a model. In Michalos’ terms, a decision maker has to choose between different possible and mutually exclusive hypotheses, trying to elucidate which one is the most adequate for his interests . In order to make this decision, the decision maker has to determine the “raw forms” of the benefits and costs attached to each combination.

For example, he must be able to determine whether two hypotheses are equally explanatory or one explains more than the other; he must be able to rank order any three distinct levels of explanatory power transitively; and he must recognize that his preferences ought to prefer a hypothesis that explains more phenomena to one that explains less (if all other things are equal) (Michalos 1970, 64). Among benefits, the decision maker can take into account such things as “explanatory power, simplicity, coherence with other theories, precision, etc.” (Michalos 1970, 64). And costs will be such things as “required set-up time, computational effort, special facilities, technical assistance, money, operationalization, etc.” (Michalos 1970, 65). In general terms, a model is better than its alternatives depending on the benefits and costs of accepting it. ³⁷ Scientists will choose between attributes that they consider especially relevant. “For our purposes it is not necessary to reach an agreement on the optimal set of appraising attributes” (Michalos 1970, 74). There is a tendency for decision-makers to assess some attributes as more important than others in order to determine their final judgment. The reasons for doing that will depend on the general purposes that scientists have to consider in order to generate models. In the case of strength of materials, when engineer-scientists have to propound the best model for their goals, they need to weigh up the benefits and costs of the available models, and they, like any other scientist, will prefer those models with more benefits and less costs. The main difference between engineer-scientists and scientists in basic areas are the benefits that they consider more important to fulfill, as well as the costs that they try to avoid.

A criticism against this suggestion could be that it mixes up some values commonly considered as epistemic and others that are commonly considered pragmatic. Nevertheless, as Duhem, Popper, or Carnap made clear a long time ago, the borderline between pragmatic and epistemic values may be difficult to draw, since pragmatic reasons are as important as epistemic ones in scientific development. In this sense, instead of differentiating the attributes between epistemic and pragmatic, perhaps it could be more suitable to refer to them as values (as a desirable property) or non-values (as a non desirable property).

4.5. Desirable attributes for strength of materials.

Engineer-scientists’ models have to fulfill some values in order to represent some aspects of reality in the most accurate way considered relevant for engineers’ purposes. In order to decide which model is the best (with more desirable attributes), engineers can apply the general principle of costs and benefits, referred to now as desirable and non-desirable attributes. Let’s analyze some of the most important attributes that models have to fulfill for the purposes of strength of materials.

(1) Internal consistency: Every scientific theory has to be consistent from an internal point of view. From the same principles it cannot be possible to infer A and ¬A. If strength of materials were not internally consistent, then the suggested equations would provide contradictory conclusions, and the artifacts built would be inefficient, and non-safe.

(2) Empirical adequacy: Strength of materials models have to be adequate with respect to the empirical facts. Despite the fact that the models are not isomorphic with reality, they try to explain some observable properties of materials. Sometimes, the empirical adequacy of strength of materials is not the same as that provided by theoretical models from basic sciences. The reason for this contradictory feature is the different properties both sciences are trying to analyze. Strength of materials analyzes the effects of loads on the internal structure of bodies. From physicists’ point of view, all bodies are perfectly rigid, and the shape of bodies does not change under the action of external loads. These deformations do not affect the general laws of equilibrium or the motion of bodies; that is why they are not taken into account in theoretical mechanics. Nevertheless, bodies do change, but these deformations are so small that physicists can abstract from them (transforming them into ceteris paribus clauses), because they do not affect the general laws of equilibrium and the movement of bodies. But, as a matter of fact, all the shapes of material bodies change when they are subjected to external loads, something that must be acknowledged in order to build safe constructions.

Strength of materials models simplify and abstract other properties in an unacceptable way from the point of view of basic sciences. For instance, materials are considered as homogeneous and continuous despite the well known fact that no materials are actually homogeneous because of their molecular composition. Materials are usually considered isotropic , something that is not true for every material. However, from the point of view of engineering sciences materials behave as if they were homogeneous, continuous, and isotropic.

(3) Accuracy: Strength of materials models, instead of generating accurate values about the behavior of bodies, create sets of limit values, among which decisions must be made.

When different loads are studied, examples at different points are analyzed in order to know how the loads affect a wide range of materials with different shapes. Engineers commonly use security coefficients when applying the models to real building instances. When the real behavior of materials and bodies with different shapes is not accurately known, and the law can only provide with some approximation, then some maximum and minimum safe values are offered.

(4) Fruitfulness: From a relatively small set of theoretical principles (stress, strain, load, Hooke’s law, Saint-Venant’s principle…), engineers who develop strength of materials equations try to suggest a range of specific models. Strength of materials models have to be fruitful in order to generate an adequate comprehension of the behavior of different materials. That is the reason why strength of materials calls for applied mathematical models rather than the more abstract models found in natural scientific theories, and why experimental work is done on different kinds of materials and body shapes. ³⁸

(5) Explanatory power: Strength of materials models have to be explanatory with respect to some properties of materials. Models must be explanatory in the sense of generating general principles that correctly characterize the behavior of the materials. That is the case, for instance, of Hooke’s law or Saint-Venant’s principle. Some philosophers have considered explanatory power as the main goal in scientific activity. Nevertheless, those who develop engineering sciences need to bear in mind the practical goal of their activity. That is, engineering theories have to be explanatory in order to be useful for designing artifacts.

(6) Prediction of surprising results: Strength of materials models, instead of predicting surprising results, try to avoid the emergence of this kind of outcomes when models are used generating artifacts. In some sense, it could be said that those surprising non-desired results are foreseen; at least an attempt is made to foresee them. The risk of building a failed artifact can involve an unacceptable cost. ³⁹

To approve a hypothesis or model as a basis for a specific kind of action is an important desirable feature in engineering sciences. Some philosophers would argue that this is not part of theoretical science, strictly speaking. ⁴⁰ That could be true for those theories that are not conceived with a practical goal in mind, theories that could or could not be applied in the future. The difference here is that the main concern for basic scientific models is to explain with generality, whereas the main concern for engineering scientific models is to be useful in some phase of designing artifacts. The applicability is a desired attribute, and the risks of applying an unsafe model cannot be run.

(7) Novelty: There are “models or theories that differ in significant ways from presently accepted theories, either by postulating different entities and processes, adopting different principles of explanation, incorporating alternative metaphors, or by attempting to describe and explain phenomena that have not previously been the subject of scientific investigation” ( Longino 1996 , 45). Strength of materials models differ in significant ways from physics models, postulating different entities and characteristics, such as homogeneity and continuity of material, and processes, as well as different stresses and strains that different bodies can bear without deforming. Thus, models of strength of materials describe and explain phenomena that had not previously been the subject of scientific investigation. Moreover, those models make possible investigations during the production of new materials, and the application of generated knowledge to new artifacts, another sense of novelty.

(8) Ontological heterogeneity: “A theory characterized by ontological heterogeneity (or ontological diversity) is one that grants parity to different kinds of entities”( Longino 1996 , 46). This attribute is fulfilled in strength of materials models. As mentioned in the earlier discussion about empirical adequacy, strength of materials researchers do not only suggest models about materials in general, but about specific materials and for specific shapes of them, in different temperatures and load conditions.

(9) Applicability to current human affairs: This kind of attribute is essential for engineering science models, and in many senses it conditions other desirable attributes. For instance, empirical adequacy can be understood as regarding different properties of matter not considered relevant for basic sciences; accuracy can be proposed within a range (or spectrum) of different safe possibilities instead of looking for idealized and abstract values, or the outcome of ceteris paribus clauses inappropriate for the applicability purposes of strength of materials; surprising results have to be avoided, because the by-product risk of building a failed artifact can involve an unacceptable cost; the kind of phenomena that are interesting from a strength of materials models point of view are more heterogeneous than the kind of phenomena that are interesting from a basic sciences point of view; that is, the ontology is more heterogeneous for the engineering sciences because different materials behave in very different ways, something that must be known in order to build artifacts with them. In other words, the main concern of strength of materials models is to solve problems arising during designing activities, and to open up new possibilities.

The search for applicability also determines some attributes, otherwise described by philosophers as necessarily desirable, to become less important for strength of materials models. For instance:

(1) Simplicity: Strength of materials models could give up simplicity, and ontological heterogeneity, for applicability to current human affairs, a more desirable attribute from the engineer’s point of view.

(2) External consistency: Strength of materials models are proposed in spite of their inconsistency with models from well established basic sciences. Engineers can overlook external inconsistencies with physics, because they result from basic simplifications and idealizations regarding the relevant properties that different sciences try to analyze.

(3) Scope: Strength of materials models can renounce breadth of scope for models that fulfill the aim of ontological heterogeneity. In order to accomplish breadth of scope, basic scientists may need to use ceteris paribus clauses that avoid the heterogeneity and dynamic aspects of the real world. But this tactic is used (carefully) in strength of materials models, because engineers who develop and use theoretical or mathematical models need to apply them to real situations and they need to avoid surprising (or catastrophic) results.

Disparities between the desirable values in strength of materials and desirable values in the basic sciences depend on the goals that engineers and basic scientists have to fulfill when developing their models. The way that engineers weigh desirable values decides some features of their models. Generally speaking, engineering sciences are part of a complex technological system, whose main goal is not to know how things are (typical on a scientific system), but to build useful artifacts. Applicability to current human affairs is the main goal pursued by engineers, and it yields different ways of weighing the costs and benefits of suggested models. If there are differences between engineering science models and basic science models they will be found in the evaluation of desirable attributes; in the final analysis, in their differing goals.

Conclusions

Defining technology as applied science underestimates the complex nature of technology. Technology demands knowledge that does not come from traditional scientific theories. Not every scientific theory can be applied to obtain technological developments. There are many scientific results, and not all of them have technological applications. Even though some natural scientific theories are applied to technological purposes, the process of applying scientific theories to produce technological devices (given technological complexity nowadays) has never been satisfactorily explained. Nonetheless, it is plausible to think that there must be theoretical science knowledge involved in contemporary technology.

This paper has tried to suggest some good reasons why engineering sciences can be included in the scientific category. It is possible to offer a characterization of the engineering sciences using an explanation originally proposed for natural scientific theories. Engineering sciences have, nevertheless, a significant difference: those who have developed these technological theories are engineers, and from the constructivist point of view it could be said that the attributes that their models have to fulfill (attributes they consider desirable) could be different from desirable attributes in basic science models.

With the aim of illustrating this, the case of strength of materials has been analyzed. The features of this engineering theory have been examined using Giere’s semantic and model-based frame. The theory can be understood as a cluster of models that represent, with different degrees of similarity, different aspects of reality. The main differences between basic scientific theories and strength of materials are based on the purposes of the engineers who develop the theory and who use it afterwards. In general, it is possible to say that scientists’ main purpose is “to know how things are,” whereas engineers developing strength of materials would add “in order to make other things work.”

A final caveat: Some critics could claim that the use of cost-benefit analysis as a criterion for choosing between different models could lead to an instrumentalist point of view of scientific theories; the relevance of models depends on their capability for fulfilling different benefits determined “in a raw form” by scientists. Does this imply relativism? I do not think so. Defenders of relativistic positions about scientific theories can maintain that, as with any other human creation, scientific theories have no more than a relative value. However, from the perspective suggested in this paper, scientists develop models in order to achieve goals. If there is any rationality when scientists develop a best model, a model that better fits with reality, it has to be a conditional or instrumental rationality. Engineers also have to develop a best model, and so they use an instrumental rationality considering their purposes. However, the differences between these purposes lead to differences between the values (or desirable attributes) which are to be fulfilled by the models; and that is the main difference between engineering science models and basic science models.

This approach could be used to analyze other technological theories. Paul T. Durbin thinks so and uses it to understand genetic engineering (see Durbin 2005 ), and the author of this article seeks to apply the approach to Artificial Intelligence, specifically to mobile robotics. Of course, every cluster of models will show peculiar features, but all engineering science models share the necessity of combining two purposes: “to understand” and to do so “in order to create technological artifacts.”

Author’s Note : This work has been supported by a post-doc grant from the Spanish Department of Education. I am very grateful to Paul T. Durbin and Óscar Martínez for their insightful comments on an earlier draft of this paper, and to Jack T. Chen for his help to improve my English. I am also very grateful to Fred Adams for his kindness and hospitality during my time as a research fellow in the Philosophy Department at the University of Delaware.

References

Agassi, Joseph. 1980. Between Science and Technology. Philosophy of Science 47: 82-99.

_____. 1985. Technology: Philosophical and Social Aspect . Dordrecht: Kluwer.

Baird, Davis. 2000. The Thing-y-ness of Things: Materiality and Spectrochemical Instrumentation, 1937-1955. In The Empirical Turn in the Philosophy of Technology . Edited by P. Kroes & A. Meijers. Amsterdam: JAI Elsevier Science.

_____. 2001a. Thing Knowledge: A Philosophy of Scientific Instruments . Berkley, CA: Univ. of California Press.

_____. 2001b. The Knowing of Things. In Controlling Technology . Edited by E. Katz, A. Light & W. Stevens. New York: Prometheus Books.

_____. 2002. Thing Knowledge. Function and Truth. Techné: Journal of the Society for Philosophy and Technology 6.2 .

Bucciarelli, Louis L. 1988. Engineering Design Process. In Making Time: Ethnographies of High Technology Organizations . Edited by P. Dubiaskas. Philadelphia: Temple Univ. Press.

_____. 1994. Designing Engineers . Cambridge, Mass: MIT Press.

Bunge, Mario. 1966. Technology as Applied Science. Technology and Culture 3: 329-347.

_____. 1967. Scientific research . New York: Springer-Verlag. Cartwright, Nancy. 1983. How the Laws of Physics Lie . Oxford: Clarendon Press.

_____. 1996. Models: The Blueprints for Laws. Philosophy of Science 64: S292-S303.

Chakravartty, Anjan. 2001. The Semantic or Model-Theoretic View of Theories and Scientific Realims. Synthese 127: 325-345.

Churchland, Paul. 1985. The Ontological Status of Observables: In Praise of the Superempirical Virtues. In Images of Science . Edited by Paul Churchland and Clifford Hooker. Chicago, IL: University of Chicago Press.

Constant, Edward W. II. 1980. The Origins of the Turbojet Revolution . Baltimore: The Johns Hopkins Univ. Press.

_____. 1999. Reliable Knowledge and Unreliable Stuff. Technology and Culture 40: 224- 257.

Cuevas-Badallo, Ana. 2003. Las ciencias ingenieriles como ‘ciencias para la aplicación’. El caso de la resistencia de materiales. Argumentos de la Razón Técnica 6: 161-180.

_____. 2005. The many faces of science and technology relationships. Essays in Philosophy . (January) 6.1.

De Vries, Marc J. 2003. The Nature of Technological Knowledge: Extending Empirically Informed Studies into GAT Engineers Know. Techné: Journal of the Society for Philosophy and Technology 6.3.

Drucker, Peter Ferdinand. 1961. The Technological Revolution. Notes on the Relationship of Technology, Science and Culture. Technology and Culture 2: 342-351.

_____. 1963. Modern Technology and Ancient Jobs. Technology and Culture 4: 277-281.

Durbin, Paul T. 2005. Toward a Philosophy of Biotechnology, a paper presented at the 14th international conference of The Society for Philosophy and Technology (Delft, July 2005).

Feibleman, James K. 1966. Technology as Skills. Technology and Culture 3: 318-328.

Feodosiev, Vladimir. 1968. Strength of Materials . Moscow: Mir.

Freeman, Cristopher. 1982. The Economics of Industrial Innovation . London: Pinter.

Giere, Ronald N. 1969. Comments on Braithwaite. In Science, Decision and Value . Edited by James Leach, Robert Butts and Glenn Pearce. Dordrecht: D. Reidel Pub. Company.

_____. 1988. Explaining Science: A Cognitive Approach . Chicago: Univ. of Chicago Press.

_____. 1992. Cognitive Construction of Scientific Knowledge. Social Studies of Science 22: 95-107.

_____. 1993. Science and Technology Studies: Prospects for an Enlightened Post-Modern Synthesis. Science, Technology, and Human Values 18: 102-112.

_____. 1994. Cognitive Structure of Scientific Theories. Philosophy of Science 61: 276-96.

_____. 1996. The Feminist Question in the Philosophy of Science. In Feminism, Science and the Philosophy of Science . Edited by L. Hankison Nelson and J. Nelson. London: Kluwer Academic Publishers.

_____. 1999a. Science without Laws . Chicago: Univ. of Chicago Press.

_____. 1999b. Using Models to Represent Reality. In Model-Based Reasoning and Scientific Discovery . Edited by L. Magnani, N. J. Nersessiand & P. Thagard. New York: Kluwer/Plenum.

_____. 2002. Discussion Note: Distributed Cognition in Epistemic Cultures. Philosophy of Science 69: 637-644.

_____. Forthcoming (1). How Models Are Used to Represent Reality. Philosophy of Science .

_____. Forthcoming (2). Perspectival Pluralism. Minnesota Studies in Philosophy of Science 19.

Hall, Alfred Rupert. 1962. The Technical Act. The Changing Technical Act. Technology and Culture 3: 501-515.

Hesse, Mary. 1966. Models and Analogies in Science . Notre Dame: Notre Dame Univ. Press.

Ihde, Don. 1991. Instrumental Realism . The Interface between Philosophy of Science and Philosophy of Technology. Bloomington: Indiana Univ. Press.

Ilyushin, A. A., Lensky, V. S. 1967. Strength of Materials . Oxford: Pergamon Press.

Kuhn, Thomas S. 1970. The Structure of Scientific Revolutions . Chicago: The Univ. of Chicago Press. Enlarged.

_____. 1977. The Essential Tension . Chicago. IL: University of Chicago Press.

Lange, Richard. 2003. Technology as Basis and Object of Experimental Practice. In The Philosophy of Scientific Experimentation . Edited by H. Radder. Pittsburgh: Pittsburgh Univ. Press.: 119-137.

Laudan, Larry. 1990. “Demystifying Underdetermination.” In Minnesota Studies in the Philosophy of Science . Vol. XIV: Scientific Theories. Edited by C. Wade Savage. Minneapolis, MN: University of Minnesota Press.

Laymon, Richard. 1989. Applying Idealized Scientific Theories to Engineering. Synthese 81: 353-371.

_____. 1991. Idealizations and the Reliability of Dimensional Analysis. In Critical Perspectives on Nonacademic Science and Engineering . Edited by Paul T. Durbin. Cranbury, NJ: Lehigh University Press.

Layton, Edwin T. 1971. Mirror Image Twins: The Communities of Science and Technology in 19th Century America. Technology and Culture 19: 562-580.

_____. 1973. A Historical Definition of Engineering. In Technology and Social Change in America . Edited by E. Layton. Harper and Row, New York: 60-79.

_____. 1974. Technology as Knowledge. Technology and Culture 15: 31-41.

_____. 1976. Technology and Science or ‘Vive la Petite Diference ’ PSA 2: 173-184.

_____. 1978. Millwrights and Engineers, Science, Social Roles, and the Evolution of the Turbine in America. In The Dynamics of Science and Technology . W. Krohn, E. T. Layton, P. Weingart. D. Reidel: Dordrecht, 61-88.

_____. 1979. Scientific Technology, 1845-1900: The Hydraulic Turbine and the Origins of American Industrial Research. Technology and Culture 20: 64-89.

_____. 1984. Science and Engineering Design. In Bridge to the Future. A Centennial Celebration of the Brooklyn Bridge, Annals of the New York Academy of Sciences . Vol. 424. Edited by M. Latimer, B. Mindle, and M. Kranzberg. New York: The New York Academy of Sciences.

_____. 1987. Through the Looking Glass, or News from Lake Mirror Image. Technology and Culture 28: 594-607.

_____. 1988. Science as a Form of Action: The Role of the Engineering Sciences. Technology and Culture 29: 82-97.

Longino, Helen. 1990. Science as Social Knowledge . Princeton, NJ: Princeton University Press.

_____. 1996. Cognitive and Non-Cognitive Values in Science. In Feminism, Science and the Philosophy of Science . Edited by L. Hankison Nelson and J. Nelson. London: Kluwer Academic Publishers.

McMullin, Ernan. 1982. Values in Science. PSA 2: 3-28.

Mitcham, Carl. 1991. Engineering as a Productive Activity: Philosophical Remarks. In Critical Perspectives on Nonacademic Science and Engineering . Edited by Paul T. Durbin. Cranbury, NJ: Lehigh University Press.

Morrison, Margaret. 1999. Models as Mediators: Perspectives on Natural and Social Sciences . Cambridge: Cambridge Univ. Press.

Nagel, Ernest. 1961. The Structure of Science . New York: Harcourt, Brace & World Inc.

Nelson, Richard P. 1982. The Role of Knowledge in R&D Efficiency. Quarterly Journal of Economics 338: 453-70.

Niiniluoto, Ilkaa. 1995. Approximation in Applied Science. In Structuralism, Approximation, and Idealization . Poznan Studies in the Philosophy of the Sciences and the Humanities, Vol. 42. Edited by M. Kuokkanen.

Petroski, Henry. 1992. The Evolution of Useful Things . New York: Vintage Books.

_____. 1996. Inventing by Design. How Engineers get from Thought to Thing . Harvard Univ. Press.

Pisarenko, G. S., Yakovlel, A. P., Matveev, V. V. 1975. Manual de resistencia de materiales . Moscú: Mir.

Pitt, Joseph C. 2000. Thinking about Technology. Foundations of the Philosophy of Technology . New York: Seven Bridges Press.

_____. 2001. What Engineers Know. Techné: Journal of the Society for Philosophy and Technology 5.3.

Putnam, Hilary. 1975. Mathematics, matter, and method . New York: Cambridge Univ. Press.

Quintanilla, Miguel Ángel. 1998. Technical Systems and Technical Progress: A Conceptual Framework. Techné: Journal of the Society for Philosophy and Technology 4.1.

Radder, Hans. 1996. In and About the World. Philosophical Studies of Science and Technology . New York: State University of New York Press.

Rapp, Friedrich. 1981. Analytical Philosophy of Technology . Dordrecht: Boston Studies in Philosophy of Science, vol. 63.

Rosenberg, Nathan. 1982. Inside the Black Box. Technology and Economics. Cambridge: Cambridge Univ. Press.

Sandor, Bela Imre. 1978. Strength of Materials . Englewood Cliffs: Prentice Hall.

Simon, Herbert. 1945. Administrative behavior . New York: Free Press.

Smart, John Jamieson C. 1963. Philosophy and scientific realism . New York: Humanities Press.

Singer, Ferdinand L. 1951. Strength of Materials . New York: Harper & Row Pub.

Stepin, P. A. 1963. Strength of Materials . New York: Gordon and Breach.

Suppe, Frederick. 1989. The Semantic Conception of Theories and Scientific Realism . Chicago: Univ. of Illinois Press.

Teller, Paul. 2001. Twilight of the Perfect Model Model. Erkenntnis 55: 393-415.

Timoshenko, Stephen P. 1930. Strength of materials . New York: D. Van Nostrand Company, Inc.

_____. 1953. History of Strength of Materials . New York: McGraw-Hill.

Timoshenko, Stephen P., Gleason Harvey. 1935. Elements of Strength of Materials . MacCullough. New York: D. Van Nostrand Company, Inc.

Todhunter, Issac. A History of the Theory of Elasticity and the Strength of Materials. From Galileo to the Present . London: Dover.

Tondl, Ladislav. 1973. Scientific Procedures; a Contribution Concerning the Methodological Problems of Scientific Concepts and Scientific Explanation . Boston: Dordrecht Reidel Pub.

Vincenti, Walter G. 1984. Technological Knowledge without Science: the Innovation of Flush Riveting in American Airplanes, ca. 1930-ca. 1950. Technology and Culture 25: 540-576.

_____. 199 0. What Engineers Know and How They Know It. Analytical Studies of Aeronautical History . Baltimore: The Johns Hopkins Univ. Press.

_____. 2001. The Experimental Assessment of Engineering Theory as a Tool for Design. Techné: Journal of the Society for Philosophy and Technology 5.3.

Willems, Nicholas. Easley, John T. Rolfe, Stanley T. 1981. Strength of Materials. New York: McGraw-Hill.

¹ The author of the article is non-native English speaker. For this reason, she would like to ask for forgiveness for those errors and mistakes she could commit writing the article.

² Pitt 2000 ; Radder 1996 .

³ Giere, 1988 , 1992 , 1993 , 1994 , 1999a , 1999b , 2002 , forthcoming (1) , and forthcoming (2) .

⁴ We also could include here T. Kortabinski, H. Rumpf, G. Ropohl and others, but the cited authors are representative of the main ideas on the subject.

⁵ See Constant, 1980 .

⁶ Just to mention a classic: “Science as an institutionalized art of inquiry has yielded varied fruit. Its currently best-published products are undoubtedly the technological skills that have been transforming traditional forms of human economy at an accelerating rate.” (Nagel 1961 , vii). In the same vein we could see too the “miracle argument” by J. J. C. Smart, 1963 and Hilary Putnam, 1975 . A more recent contribution is Radder’s view: “Concerning experimental natural science as such, I think two legitimations play a fairly prominent and general role. The first is the claim that science is valuable because it delivers the truth about nature or, at least, promises to eventually give a true account of nature. The second major social legitimations is framed in the claim that experimental science is practically useful, that its results can often be fruitfully incorporated into all kinds of technological projects. (…) Actually, in present-day society, the “technological” legitimations seems to be the most influential.” (Radder 1996 , 40).

⁷ For a broader explanation and discussion: A. Chakravartty 2001 .

⁸ For a historical review: Suppe 1989 .

⁹ For instance: Giere 1988 , 92.

¹⁰ He deliberately says that the natural laws are not universal, nor necessaries, nor truth. ( Giere 1999 , 90).

¹¹ These ideas derive from pragmatism ( Giere 1999 , 75). In philosophy of technology we could find something similar in: Pitt 2000 , 4.

¹² For instance: Giere 1999a , 180.

¹³ He agrees with N. Cartwright (1983, 11), “No single model serves all purposes best.” (Also in p. 104 and 152). “Imagine the universe as having a definite structure, but exceedingly complex, so complex that no models humans can devise could ever capture more than limited aspects of the total complexity. Nevertheless, some ways of constructing models of the world do provide resources for capturing some aspects of the world more or less well. Other ways may provide resources for capturing other aspects more or less well. Both ways, however, may capture some aspects of the reality and thus be candidates for a realistic understanding of the world. So here, in principle, is a solution to the problem of finding a picture of science that is both naturalistic and realistic.” ( Giere 1999a , 79).

¹⁴ Against the idea that “much engineering knowledge is ‘cookbook engineering’.” (Pitt 2000 , 38).

¹⁵ I have decided to use several textbooks from different periods instead of only one in order to avoid a biased presentation.

¹⁶ This is not the same as defending that these theories are inferior from the point of view of their epistemological features.

¹⁷ This supposition is adopted despite the well known fact that no material can really be homogeneous because of their molecular composition. Moreover, the textbooks later analyze materials’ fragility and the homogeneity supposition will be questioned.

¹⁸ Actually, this characteristic does not correspond with real properties of most materials. Every crystal is no isotropic, but if the body contains great deal of chaotically oriented crystals it can be considered as isotropic.

¹⁹ In some textbooks, instead of four, one can find three basic forms. In these cases it is supposed that vaults are special types of plates.

²⁰ “The internal forces must be distributed over the section that the deformed surfaces of the section A are a perfect fit when the right and the left portions of the body are brought together. In strength of materials and in the theory of elasticity this condition is known as the condition of continuity of deformations.” ( Feodosiev 1968 , 2s).

²¹ “The purpose of the analysis is to decide whether or not the structure meets the requirements of reliability” ( Feodosiev 1968 , 31).

²² Robert Hooke, curator of the Royal Society, originally laid down this principle in 1679, saying “ut tensio, sic vis.”

²³ ( Stepin 1963 , 114) Shafts, spindles of turning lathes, and jackhammers and other pieces work with torsion (Pisarenko et al. 1975 , 7-8).

²⁴ Many elements of structures work by tension or compression, framework beams, columns, shoot of piston machines, bolts for tightening…etc. (Pisarenko et al. 1975 , 7-8).

²⁵ Instances of deflection are beams of intermediate flats, of bridges, axis in train coaches, springs, shafts, gear teeth, wheels’ spokes, levers, etc. (Pisarenko et al. 1975 , 7-8).

²⁶ “The objective of strength of materials is not only to reveal the inherent features of phenomena but also to provide background for the correct interpretation of the laws so obtained in the assessment of efficiency and serviceability of the structure under consideration.” ( Feodosiev 1968 , 14).

²⁷ Willems, Easley, Rolfe 1981 , 385.

²⁸ Engineers often make a lengthy use of their textbooks because they can use these useful tables in their professional life when designing concrete artifacts.

²⁹ This is certainly and extremely abbreviated account, just the minimum to present the theory in some textbooks. Of course, every one who is interested in other details should read the cited textbooks.

³⁰ Ronald Laymon has worked on this matter. See, for instance: Laymon 1989 , 1991 .

³¹ This idea is suggested by Giere, Morrison, and Teller, although neither of them apply it to the case of engineering sciences.

³² In some texts the basic forms are four, and in others three. In this case, vaults are considered as special cases of plates.

³³ “The margins of error rarely appear in the descriptions or calculations until one gets to the point of comparing theoretical predictions with actual measurements. This practice strongly supports interpreting the original equations without explicit margins of error, as referring not to actual things but to abstract models of which they are true by definition.” ( Giere 1999b , 6).

³⁴ Radder examines three types of reproducibility in experimental practice: (i) Reproducing the material realization, (ii) Replication of the experimental result, and (iii) reproducing under a fixed theoretical description. (1996, 20-28). Lange analyzes different ways of knowledge acquisition in order to do reproducible experiments: “Communication and cooperation ensure the synchronomous extensibility of experimental practice in space, specialist education ensures their diachronous persistence.” ( 2003 , 133)

³⁵ However, this is not the only motive used to choose among models. As a matter of fact, Giere claims “what is essential is that scientists have other interests as well, and that these play a significant role in scientific decisions. As I understand it, a cognitive theory of the science need not deny the importance of these other interests. If it did it, it could not be an adequate theory of science.” ( Giere 1988 , 165).

³⁶ Thomas S. Kuhn ( 1977 ) discusses five features that scientist use choosing between theories: accuracy, consistency (both internal and with other relevant currently accepted theories), scope (its consequences should extend beyond the data it is required to explain), simplicity (organizing otherwise confused and isolated phenomena), and fruitfulness (for further research). Helen Longino ( 1990 ) distinguishes between constitutive and contextual values, being the constitutive ones: empirical adequacy, simplicity, and explanatory power. Larry Laudan ( 1990 ) points out another catalog of characteristics: internal consistency, the prediction of surprising results, and variety of evidence. Paul Churchland ( 1985 ) identifies simplicity and explanatory power as cognitive or epistemic virtues that enable us to go beyond mere empirical adequacy. Longino ( 1996 ) reveals a feminist’s set of desiderata in scientific theories: empirical adequacy, novelty, ontological heterogeneity, mutuality of interaction, applicability to current human needs, and diffusion of power.

³⁷ “If for every possible contingency and for every attribute, the benefits and costs of accepting one hypothesis are preferable (i. e., ought to be preferred) to those of accepting another, then the former strongly dominates the latter. If for some contingency and for some attribute, the benefits and costs of accepting one hypothesis are preferable to those of another and for all the remaining contingencies and attributes the benefits and costs of accepting the latter are not preferable to those of the former, then the former dominates the latter.” (Michalos 1970, 65)

³⁸ “As we have already noted, the introduction of iron and steel into structural and mechanical engineering made experimental study of the mechanical properties of those materials essential. Earlier experimenters had usually confined their attention to determining ultimate strengths, but it was now realized that the properties of iron and steel depend upon the technological processes involved in manufacture and that, in any case, a knowledge of ultimate strength only is insufficient when selecting a suitable material for a particular purpose. A more thorough investigation of the mechanical properties of materials became of utmost practical importance. Such tests require special equipment, and we shall see that in the period under consideration a rapid growth of material-testing laboratories took place in many countries.” (Timoshenko 1953 , 276)

³⁹ As Richard Rudner argued about the acceptance of a scientific hypothesis: “Is going to be a function of the importance, in the typically ethical sense of making a mistake in accepting or rejecting the hypothesis. Thus, to take a crude but easily manageable example, if the hypothesis under consideration were to the effect that a toxic ingredient of a drug was not present in the lethal quantity, we would require a relatively high degree of confirmation or confidence before accepting the hypothesis, for the consequences of making a mistake here are exceedingly grave by our moral standards.” (Rudner 1953, 2) Related to engineering sciences, this kind of analysis is of a great relevance.

⁴⁰ “If theory is being applied to practical ends, and the theoretical alternatives carry with them outcomes of different value to the agents concerned, we have the typical decisiontheoretic grid involving not only likelihood estimates but also “utilities” of one sort or another. Such utilities are irrelevant to theoretical science proper and the scientist is not called upon to make value-judgments in their regard as part of his scientific world.” ( McMullin 1982 , 8).

by ck