JTE v24n1 - Transfer of Learning: Connecting Concepts During Problem Solving
Transfer of Learning: Connecting Concepts During Problem Solving
Raymond A. Dixon and Ryan A. Brown
A concern of many educators and managers is students’ ability to transfer concepts and procedures learned in school to the work environment. According to the Committee on Science (2007) the high school experience does not provide enough authentic problem-solving and project-based activities for students to be prepared mentally for the types of problems they will have to solve in the real world, or at their place of employment. When children are taught a skill, such as solving a mathematical problem, they often fail to recognize that their new skill can be used to solve a similar problem outside of school ( Bereiter, 1984 ). In other cases, students who are skilled with certain tasks outside of school often have difficulty transferring concepts learned from these experiences ( Lave, 1988; Johnson, 1997 ; Johnson, Dixon, Daugherty, & Lowanto, 2011 ) to the solving of well-structured problems in schools, such as those often found on mathematics and science tests. These findings demonstrate the inability of students to recognize the transferability of concepts learned from solving well-structured problems in the classroom to ill-structured problems faced outside of the classroom and also the transferability of concepts learned from solving ill-structured problems, similar to those encountered in the real world, to the solving of well-structured problems encountered in the classroom.
Brophy, Klein, Portmore, and Rogers (2008) are of the opinion that we have to urgently change the way in which we teach students in order to address their inability to effectively transfer concepts. The changing nature of work accentuates the need for this radical shift. In order to mitigate the need for extensive retraining at great cost to organizations it is critical that workers are able to transfer their knowledge to new situations quickly and efficiently ( Johnson, 1995 ). Various curricula and outreach programs, such as Design, Technology, and Engineering for All Children, Engineering by Design™, Project Lead the Way, Engineering is Elementary®, LEGO® Engineering, and others, offer various types of problem-based and project-based experiences, which engage students in authentic problem solving ( Jeffers, Safferman, & Safferman, 2004 ). These learning initiatives help to improve students’ ability to transfer knowledge, concepts, and skills learned in schools to real-life contexts. Some of these curricula, such as Engineering by Design™ and Project Lead the Way, use engineering principles and design as a framework for learning STEM concepts and processes ( Nathan, Tran, Phelps, & Prevost, 2008 ). The ontology of engineering education provides a framework that supports the acquisition of a wide range of knowledge and skills that are associated with STEM.
The low performance of students on standardized tests, however, is still a major concern for educators and the general public. While these curricula offer more authentic problem solving, it is not clear if these experiences also allow students to connect learned concepts to the solving of mathematics and science standardized test items. This study focuses on one such curriculum—Project Lead the Way (PLTW)—a multi-year, problem-based/project-based pre-engineering curriculum that is used by some schools in their engineering and technology education program ( Tran & Nathan, 2010 ). Since a large portion of the PLTW objectives emphasize content from mathematics and/or science standards ( Project Lead the Way [PLTW], 2008 ), it is the authors view that students should be able to demonstrate the ability to connect concepts learned from engaging in PLTW curriculum activities to the solving of mathematics and science test problems in the classroom.
Purpose of the Study
The purpose of this study is to determine if PLTW students are able to better transfer mathematics, science, and design concepts from one situation to another than students who have not taken the PLTW courses and the extent to which students are able to make connections to concepts learned in the PLTW courses to concepts that they are required to use when solving standardized test problems. This study is based around the following research questions:
- Is there a relationship between the mathematics, science, and design performance of students and the number of PLTW courses they have taken? Is there a difference in the mathematics, science, and design performance of students who have taken PLTW courses and those who have not taken a PLTW courses?
- To what extent are students able to associate concepts learned in the PLTW curriculum with concepts required to solve mathematics, science, and design problems?
Transfer of Learning
There are several factors that affect learning transfer. These include whether students understand or simply memorize knowledge, the amount of time spent on learning the task, the amount of deliberate practice that is done beyond learning the task, the motivation of the student, how the problem is represented, the transfer conditions, and the metacognition of the solver ( Dweck, 1989 ; Ericsson , Krampe, & Tesch-Romer, 1993; Johnson et al., 2011 ; Palinscar & Brown, 1984 ; Singley & Anderson, 1989 ).
Two broad categories of transfer are described in the literature—near transfer and far transfer. According to Johnson (1995) near transfer occurs when students apply their knowledge and skills in situations and contexts that are very similar to those in which the learning occurred. In contrast, a far transfer occurs when a skill is performed in a context that is very different from the context in which the skill was learned. The opportunities for far transfer in problem solving within schools are understandably not as regular as the opportunities for near transfer. Far transfer is more difficult “because students must deliberately analyze the situation in order to recall the rules or concepts that are needed to apply their knowledge and skill in that particular situation (Salomon, 1988)” (p. 34).
Good and poor problem solvers differ in their recall of information from previously encountered problems and by extension their ability to transfer concepts to the target problem. This difference exists because poor problem solvers tend to remember surface similarities between problems, while good problem solvers remember underlying conceptual structures that make two problems similar although they have different surface features ( Sutton, 2003 ). This ability of good problem solvers makes it easier to transfer concepts learned in other domains or from solving other types of problems because of their conscious effort to abstract knowledge and concepts from one context for application to another ( Johnson, 1995 ). Cognitive research shows that the organization of learning and how new learning relates to what a student already knows are the strongest predictors of how well a student will transfer knowledge ( National Research Council, 2000 ). Schunn and Silk (2011) articulated, however, that in science and engineering students often “lack relevant conceptual frameworks or have frameworks that are not developed enough to support new learning adequately” (p. 9). The absence of such frameworks makes it difficult for students to connect and apply other knowledge where relevant.
Key Components in the Learning Transfer Process
Sutton (2003) , stated that “the problem-solving process involves several aspects from which three major facets tend to emerge: the solver’s representation of the problem, the solver’s background experiences, and the solver’s understanding of the problem” (p. 56). The problem solving process begins as soon as the problem solver generates enough information about the problem space to gain an understanding of the problem. Often, the problem solver is able to associate concepts from previous experience to solving a similar problem. This association with analogous concepts may originate from some form of prompting about the similarity, or the two problems may share similar surface features that the problem solver recognizes ( Gick & Holyoak, 1980 ; Needham & Begg, 1991 ). Sometimes the problem provides retrieval cues that permit access to relevant clues that in turn aid in the transfer of concepts and knowledge. According to Perfetto, Bransford, and Franks (1983) , most problem-solving situations involve cases in which problem solvers are uninformed. They are not provided with any clues or prompt about previously learned concepts that can aid in the solution, and so they engage in self-generation of potential answers to the problem solution. That being the case, it would seem relevant that studies also address the question of how information can be transferred under a “condition in which students are not explicitly informed about a particular acquisition context that is relevant to problems they confront” (p. 31).
Representation . Representation in the problem-solving process refers to how the solver mentally represents the problem. The solver’s representation of the problem is directly related to his or her existing knowledge structure of the content of the problem. The advantages of abstract problem representations have been studied in the context of algebra word problems. “Students who were trained on specific task components without being provided with the principles underlying the problems, could do specific tasks well but they could not apply their learning to new problems. By contrast, the students who received abstract training showed transfer to new problems that involved analogous relations” ( National Research Council, 2000, p. 63 ). Research also shows that engaging students in the solutions of different types of problems in different contexts can enhance transfer by enabling learners to think flexibly about complex domains ( Spiro, Feltovitch, Jackson, & Coulton, 1991 ). Various types of mental representations are used by students and experts alike in order to understand a problem and to facilitate transfer, particularly, but not limited to, representations such as analogies, metaphors, and propositions are used in the solving of ill-structured problems such as engineering design ( Hey, Linsey, Agogino, & Wood, 2008 ; Lewis, 2008 ; Paivio, 1990 ).
Understanding . A student’s comprehension of a problem and his or her ultimate ability to transfer concepts learned previously to the current problem is inextricably linked to his or her ability to properly represent the problem. Embedded within each representation are concepts that the solver deems analogous to the problem being tackled, and he or she will transfer these concepts to arrive at a satisfying solution. A philosophical underpinning of programs that integrate the STEM domains is the learning of concepts in one domain, such as science or technology, will facilitate the learning of concepts in other domains, such as mathematics or engineering. Students who can identify the connection between concepts across domains will likely demonstrate an understanding of the problem. While a superior understanding of a problem is demonstrated by the transfer of concepts, knowledge, or processes without prompting, sometimes the use of prompting is necessary. According to Gick and Holyoak ( 1980 ; 1983) and Perfetto et al. (1983) , prompting can dramatically improve the rate of transfer in problem solving.
A good understanding of the problem will also be reflected in how solvers use metacognitive skills. Metacognition refers to how problem solvers are able to self-regulate the strategies that they use. When students are cognizant of the requirements of a problem, they will more proficiently focus on critical elements of the problem, connect or abstract common themes from previous problem solving episodes or learning experience, and evaluate their progress towards the right solution for well-structured problems or a good solution for ill-structured problems ( Sutton , 2003; National Research Council, 2000 ).
Experiences . Each student’s experience differs. Different individuals have different conceptual knowledge and will make different associations to their knowledge. Exposure to the constraints and affordances of a particular context in which a problem exists will invariably influence the way in which the student represents a problem in a similar context. According to Sutton (2003) , the solver’s prior experience helps to establish an understanding of the problem. The process of understanding is iterative, and full understanding is often complex. When the problem solver completely understands the problem and its underlying structure, then transfer to similar situations can occur.
Students bring a wealth of knowledge to each learning situation and, without specific guidance from teachers, may fail to connect everyday knowledge to subjects taught in schools ( National Research Council, 2000 ). As students’ metacognitive skills develop, their ability to make connections to their learning experiences in school and beyond the walls of the classroom becomes more self-regulated and automatic when solving problems. The nature of activities within problem-based and project-based curricula can aid in authenticating the problem-solving engagements by students so that both near and far transfer becomes more fluid. Transfer between tasks is a function of the similarity of transfer tasks and learning experiences. Transfer is therefore affected by the context of the original learning; so, people can learn in one context and yet fail to transfer in other contexts. When students are exposed to multiple contexts in their instructions that include examples that demonstrate a wide application of what is being taught, they develop a flexible representation of knowledge and are likely to abstract the relevant features of concepts that make two unique problem scenarios similar ( Gick & Holyoak, 1983 ; Spiro, Vispoel, Schmitz, Samarapungavan, & Boerger, 1987 ).
One view of learning transfer is that students find it difficult to transfer concepts that they learn in schools to the real world because education simplifies material to make it easier to teach ( Spiro et al., 1991 ). However, problem-based learning may not suffer from a lack of context or an oversimplification of content. There is a growing sentiment that learning of this form, which utilizes problem-based and project-based activities, can enhance students’ general learning transfer and problem-solving skills ( Hmelo-Silver, 2004 ). For example, Lachapelle and Cunningham (2007) found that Engineering is Elementary, one of the largest elementary engineering curricula that focuses on integrating engineering with reading literacy and existing science topics in the elementary grades, can improve students’ knowledge and comprehension of general engineering, technology, and science concepts. Mahalik, Doppelt, and Schunn (2008) , in an examination of the effectiveness of design-based instruction, found that the design-based approach for teaching middle school science is associated with improvement in science achievement, engagement, and retention of science concepts.
Project Lead the Way
PLTW is a non-profit organization that works with public schools, the private sector, and higher education to increase the quantity and quality of engineers and engineering technologists by providing high school students with engaging pre-engineering activities. They provide curricula for both middle and high schools. The standard-based pre-engineering curriculum, Pathway to Engineering, is designed for high schools. It challenges students to solve real-world engineering problems by applying their knowledge and skills in mathematics, science, and technology. The four year engineering sequence consists of eight hands-on courses; two are foundation courses (Introduction to Engineering Design and Principles of Engineering) five are specialized courses (Aerospace Engineering, Biotechnical Engineering, Civil Engineering and Architecture, Computer Integrated Manufacturing, and Digital Electronics) and one is a capstone course (Engineering Design and Development) ( PLTW, 2012 ).
A recent study by Tran and Nathan (2010) investigated the relationship between pre-college engineering studies and student achievement in mathematics. Their findings (using multilevel statistical modeling with 140 students nested within teachers) showed that while students gained in mathematics and science achievements up to tenth grade, students enrolled in PLTW foundation courses showed significantly smaller math assessment gains than those in a matched group that did not enroll, and there was no measurable advantage on science assessments when controlling for prior achievement and teacher experience.
Another study conducted by PLTW (2008) described the alignment of learning activities in PLTW curriculum, Introduction to Engineering Design (IED), with mathematics and science standards. The study showed that, generally, a large proportion of the objectives in the IED course emphasizes content from the mathematics and/or science standards, a large proportion of the objectives dually emphasize mathematics and science content, and objectives across the curriculum that emphasize mathematics and science expect students to employ concepts and skills and use short-term strategic thinking. According to PLTW, the need to show the relevance of the interconnection of STEM to what students are learning is more important than ever in order to excite more students about STEM careers.
Method
An embedded design mixed method framework ( Creswell, 2008 ) was used as the method of this study. Mixed method studies that utilize the embedded design gather both qualitative and quantitative data, but “one form of data plays a supportive role to the other form of data” ( Creswell, 2008, p. 558 ). In this study the quantitative data was given priority as the main source of data, and the qualitative data played a supportive role. This study utilized a non-experimental design, as it used intact classrooms and no attempt was made to manipulate the variables or treatment.
Participants
A convenience sample was selected. The participants were students at a Midwestern high school. The school of nearly 1,500 students is located in a rapidly growing metropolitan area on the fringe of a large city. According to the public data regarding the school, the student population is nearly 90 percent white, only two percent of the students in the district live below the poverty line, and upon graduation 90 percent of the students attend a post-secondary institution. The Engineering/Technology Education department has three full time teachers and offers a wide range of traditional technology education courses as well as six PLTW courses (Introduction to Engineering Design, Principles of Engineering, Aerospace Engineering, Civil Engineering and Architecture, Computer Integrated Manufacturing, and Engineering Design and Development). Participation in this study was offered to two upper level PLTW classes (Civil Engineering and Architecture and Engineering Design and Development) and two advanced mathematics and science classes (AP Physics and AP Calculus).
Thirty-eight students from PLTW courses and 25 mathematics and science students obtained parental consent, provided personal assent, and participated in the study. Group 1 (N = 25), referred to as non-PLTW students, consisted of students who had not taken any PLTW courses. Of this amount, 5 were juniors and the remaining 20 were seniors. All juniors had previously completed mathematics courses such as Algebra I, Algebra II, Geometry, and Trigonometry, and one student had completed a statistics course. Science courses completed by juniors included biology, chemistry, and physics. One of the juniors completed an additional AP Physics course, and another completed an additional AP Biology course. The seniors had taken additional mathematics courses such as Pre-Calculus, Calculus, and Probability and Statistics. Additional science courses taken by seniors include AP Chemistry, Zoology, Microbiology, Anatomy, AP Environmental Science, Biotechnology, and Astronomy.
Group 2 (N = 38), referred to as PLTW students, consisted of students who had completed the mathematics and science courses required of PLTW (or some of the courses, in the case of juniors and sophomores) and also more PLTW courses. Three students were sophomores, 17 were juniors, and 18 were seniors. Five students had taken two PLTW courses, 18 had taken three PLTW courses, 14 had taken four PLTW courses, and one student had taken five PLTW courses.
The groups’ sample sizes were well within the range that is required for Pearson’s correlation to detect significant correlation between two variables and for an independent t-test to detect a significant difference in students’ scores with a statistical power of .80. According to Cohen (1988) , a Pearson’s correlation test requires a minimum sample size of twenty-one for a large effect size and a one tailed alpha of .05. Also, for an independent t-test, a minimum sample size of twenty-one cases per group is needed for a large effect size and a one tailed alpha of .05.
Data Collection and Analysis
All students that consented to participate in the study were asked to complete a test instrument that was divided in three sections—mathematics, science, and design. The mathematics and science sections each consisted of five test items taken from past standardized tests. The items were then vetted by four teachers, two from mathematics and two from the sciences, to ensure consistency in the difficulty level of the test items. Answer sheets were prepared for each test item by a mathematics and science teacher. The design problem represented an ill-structured engineering problem that required students to use their knowledge of math, science, and technology to solve. The problem was adopted from an engineering design textbook. Several possible solutions were provided by the design textbook. In addition to answering the questions, the PLTW students were asked to write down the PLTW concepts or activity that best equipped them to answer each particular question. The non-PLTW students were not asked this question. Completed tests were scored by two teachers using the answer sheets that were provided.
Numerical scores were then assigned to each test section and calculated to determine an overall score. SPSS analysis of the scores found the distributions to be normal and of similar variance. A Pearson’s correlation test was then run to determine if a relationship existed between the number of PLTW courses that a student had taken and their performance on the overall test and the design, mathematics, and science components of the test. Then an independent t-test was performed to determine if a significant difference existed between the means of the PLTW students and the non-PLTW students on the overall test and each subsection. Lastly, the qualitative data was analyzed to determine if students were able to connect the concepts that were presented in the instrument with the courses in which they were presented with those concepts.
Findings
We found significant relationships between the number of PLTW courses students took and students’ performance in design score and total score. Also, there was no significant difference in mathematics and science performance between PLTW and non-PLTW students. PLTW students, however, performed significantly better on the design component of the test.
Pearson’s correlation analysis shows a significant positive correlation between the number of PLTW courses taken and the students’ score on the design component of the test (r = .33, ρ < 0.05). There was a significant positive correlation between the number of PLTW courses taken and students’ combined or total score on the test (r = .36, ρ < 0.05). In other words, the scores of the students who have taken more PLTW courses increased significantly on the design component of the test and on the total score on the test. Although these variables have statistically significant relationships, this relationship is considered weak because the number of PLTW courses only explains 11% and 13% variances of the design scores and the total scores respectively. In other words 89% and 87% of the variances in the design scores and total scores respectively can be attributed to other factors.
| # of PLTW | Total Score | Design Score | Math Score | Science Score | |
|---|---|---|---|---|---|
| # of PLTW | 1.00 | ||||
| Total Score | .35* | 1.00 | |||
| Design Score | .33* | .59** | 1.00 | ||
| Math Score | .19 | .68** | .15 | 1.00 | |
| Science Score | .18 | .72** | .17 | .17 | 1.00 |
|
**Correlation is significant at the 0.01 level (1-tailed)
*Correlation is significant at the 0.05 level (1-tailed) |
|||||
There was also a significant positive correlation between students’ total scores and their performance on the mathematics (r = .68, ρ < 0.01), science (r = .72, ρ < 0.01), and design (r = .59, ρ < 0.01) components of the test (see Table 1).
The results of the independent t-test shows a significant difference (t (df = 61) = 1.933; ρ < 0.05) between the students who have taken one or more PLTW courses and those students who have not taken any PLTW courses on the design component of the test. The PLTW students reported statistically significant higher scores on the design component of the test (x̄ = 37.82) than those who have not done the PLTW course (x̄ = 26.72); a mean difference of 11.10. There was no significant difference in the students who have taken PLTW courses and those who have not on the mathematics component (t (df = 61) = -1.43; ρ > 0.05), science component (t (df = 61) = 0.009; ρ > 0.05), and overall score on the test (t (df = 61) = 0.019; ρ > 0.05).
| Variable | N | x̄ | SD | t | ρ* |
|---|---|---|---|---|---|
| DESIGN SCORE | |||||
| Non-PLTW | 25 | 26.72 | 21.49 | 1.93 | 0.029 |
| PLTW | 38 | 37.82 | 22.79 | ||
| *One-tailed ρ value | |||||
Connecting Concepts
A qualitative assessment was done of all the PLTW students with scores at and above the 50th percentile (P 50 , N = 22) to determine the extent they were able to connect concepts that were learned from the PLTW curriculum to concepts they used to solve mathematics, science, and design items on the test. Not all students were able to explicitly identify concepts that related to the question that they were solving; however, sometimes they could remember the PLTW, mathematics, or science course in which they were introduced to the concept.
In general, the students with higher scores were able to make more connections to concepts learned from the PLTW curriculum. Figure 1 illustrates that 16% of the concepts identified in the mathematics section, 17% in the science section, and 96% in the design section of the test were connected with concepts that the students attributed to PLTW courses.
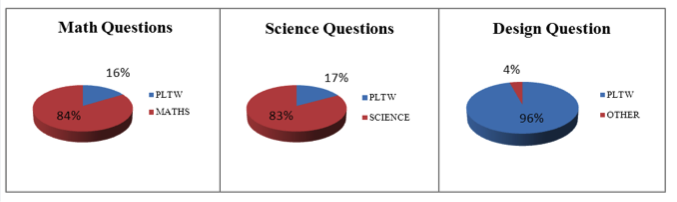
Table 3 lists the concepts and courses that students were able to make connection to when solving the mathematics, science, and design test items. Note that abbreviated concepts typically refer to courses taken in the PLTW curriculum (e.g., POE-Principle of engineering; EDD-Engineering design and development; IED-Introduction to engineering design; CEA- Civil engineering and architecture).
| Test Component | Connected Concepts | Connected Courses |
|---|---|---|
| Science Items | Electricity, Circuits, Heat transfer, Beam deflection, Beam calculation, Kinematics, Truss evaluation, V = IR, Velocity, | IDK, POE, CEA, Chemistry, Physics, Integrated Chemistry, Civil Engineering, AP Physics, Aerospace. |
| Mathematics Items | Percentage, Proportion, SOH CAH TOH, Area width & Length, Pythagoras theorem, trigonometry, Plug and play, Percentage change, Percentage error, Algebra, geometry, Law of sine and cosine, Volume | IE, POE, IDK, Middle School Math, AP Physics, Statistics, Physics |
| Design Item | Trigonometry, Problem solving, Calculus, Electricity, General math and logic, Material efficiency, Share cost projection, Design process, Geometry, | POE, IED, CEA, EDD, Physics, |
Discussion and Conclusions
Because a convenience sample was used, generalized statements about students who take and those who do not take the PLTW courses cannot be made. The findings, however, offer some insight that can be beneficial to engineering and technology educators when teaching STEM concepts. In addition, the authors believe that higher scores were possible if students were given time to prepare for the test, as is usually the norm in schools. The intent, however, was to examine students’ ability to make connections under impromptu test conditions.
A small percentage of the students in this study who performed above the 50th percentile were able to connect mathematics and science concepts (16% and 17% respectively) learned in the PLTW curriculum to the problems they were solving. The fact that students were able to identify these concepts means that they believed that these concepts were present in the PLTW courses that they had taken. Their recognition of the concepts may have allowed for greater comprehension of the problem, which likely led to more accurate solutions.
While the PLTW students’ performance was significantly better on the design question, the relationship between the number of PLTW courses taken and the scores on the design problems was weak. A possible explanation resides in the nature of the design problem, which required that students also draw heavily on their understanding of mathematics and science concepts. Therefore, topics covered in mathematics and science classes, likely, played a major part in the students’ ability to solve the design problem.
There was no significant difference in the overall performance of students in both groups on the mathematics and science items. This indicates that both groups ability to make connection to concepts from previous learning experiences when solving standardized mathematics and science test items are similar. Therefore, it can be assumed that both groups functioned at similar levels of understanding. The PLTW students, however, functioned at a superior level on the design question and the connections they made with mathematics and science concepts. Their ability to make more connections may also be indicative of superior metacognition or self-regulation. However, a research design that uses think-aloud protocols would better provide that type of evidence. Because of their higher scores on this component of the test, the PLTW students accrued higher scores on the total test.
The findings from this study are in some ways consistent with Hartzler’s (2000) findings. She conducted a meta-analysis across 30 individual studies of the effects of integrated instruction on students’ achievement. She concluded that students in integrated curricula programs outperform students in traditional class on standardized test and state testing programs. In this study, there was no difference in the performance of non-PLTW students and PLTW students on the standardized mathematics and science items. However, the PLTW students’ overall performance on the design question was higher.
Since Hartzler’s (2000) findings, more intentional efforts are being made to integrate more mathematics and science in project-based and problem-based curricula. The national demand for a STEM workforce makes integrated curricula an essential feature in education. The pedagogy of integrated STEM, however, is still in a nascent stage and more research is needed to clearly define the best strategy to optimize learning by students.
Teaching and reinforcing critical STEM concepts can be very challenging for many engineering and technology educators. While engineering and technology educators want their students to learn STEM, according to Crismond (2011, 2006) , their focus is also for students to gain competency in engineering design. Therefore, they would emphasize engineering design concepts such as optimization, tradeoff, troubleshooting, and meeting criteria within prescribed constraints. In order to increase the likelihood of students connecting and transferring STEM concepts in problem solving, engineering and technology educators will need to teach with the intent to improve students’ understanding of STEM concepts—rather than teaching primarily for the understanding of engineering concepts. Technology teachers, however, “often lack the pedagogical content knowledge that would make reviewing or re-teaching topics from STEM disciplines efficient and effective” ( Crismond, 2011, p. 299 ).
Sanders (2009) admitted that it is difficult to prepare a teacher that is competent in all three bodies of knowledge, given the volume of content knowledge necessary to be an effective science, mathematics or technology educator. Assuming Sanders’ views represent a more realistic assessment of the challenge to prepare STEM teachers, engineering and technology educators will need to work collaboratively with mathematics and science teachers to identify and teach critical STEM concepts that the engineering and technology teacher may lack the competency to teach. This will reinforce previously learned concepts and increase the likelihood of students learning and transferring difficult, abstract mathematics and science concepts and procedures. This pedagogical approach is not without its challenges, as students may still compartmentalize their knowledge. Also, it is often difficult logistically and in terms of instructional timing for teachers across STEM discipline to collaborate effectively ( Crismond, 2011 ; Kimbell & Stables, 2008 ).
Admittedly, some educators may reason that students should be able see the mathematics and the science in the engineering and technology that they teach. But students may not readily recognize these relationships unless meaningful activities are given to explicitly highlight these connections. As one young machinist admitted at the recent NSF ATE conference in Washington, DC, he did not see the relevance of trigonometry until a senior machinist showed him how to use it to solve a particular machining problem. Similarly, students may not metacognitively see the underlying links between STEM concepts and are unable to transfer the knowledge when it is needed.
Students have to increase their reflective practice to aid their metacognition and transfer of STEM concepts. Math and science concepts that are learnt during engagement with ill-defined problems can easily be forgotten because students’ short term memory is “swamped with novel design decisions that must be made and variables that must be considered” ( Crismond, 2011, p. 240 ). The engineering and technology teacher can give students activities that require them to reflect on pertinent STEM concepts—increasing their likelihood of remembering—either in groups or individually and then present their understanding to the class. Students can consult with their mathematics and science teachers, the World Wide Web, libraries, and other learning resources that can aid them in the reflective process. As Johnson (1997) purported, reflective introspection is necessary for quality learning and transfer, even if instruction occurs in rich contexts and involves interaction with peers.
Finally, this study represents a small scholarly endeavor, among many others, to examine whether problem-based and project-based curriculums such as PLTW can also help to improve students’ performance on math and science tests. However, in order to make more generalized statement about the effectiveness of these curricula, more robust experimental designs with larger random samples are necessary. In addition, other curricula need to be studied to determine their strengths and weaknesses in making explicit connections to critical math and science concepts. Until student assessment methods are modified to reflect less dependency on standardized tests, engineering and technology educators will garner greater collaboration from math and science teachers when the latter can see that engineering and design-based curriculums does improve students’ ability to solve standardized test problems.
Raymond A. Dixon ( rdixon@uidaho.edu ) is an Assistant Professor in Curriculum and Instruction at the University of Idaho. Ryan A. Brown ( rbrown@ilstu.edu ) is an Assistant Professor in Curriculum and Instruction at Illinois State University.
References
Bereiter, C. (1984). How to keep thinking skills from going the way of all frills. Educational Leadership 42 (1), 75-77.
Brophy, S., Klein, S., Portsmore, M., & Rogers, C. (2008). Advancing engineering education in P-12 classrooms. Journal of Engineering Education, 97 (3), 369-387 .
Crismond, D. (2006, October 9-12). Design's different uses in science, technology education, and math classrooms: Case studies from the US. (pp. 251-272).Paper presented at the 5 th Global Colloquium in Engineering Education, Rio de Janeiro, Brazil.
Crismond, D. (2011). Scaffolding strategies for integrating engineering design and scientific inquiry in project-based learning environment. In M. Barak & M. Hacker (Eds.), Fostering Human Development through Engineering and Technology Education (pp. 55-74). Netherlands: Sense Publishers.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.) . New York, NY: Psychology Press.
Committee on Science (2007). Rising above the gathering storm:Energizing and employing america for a brighter economic future . Washingston, DC: National Academic Press.
Creswell, J. (2008). Educational research: Planning, conducting, and evaulating quantitative and qualitative research. Upper Saddle River, NJ: Pearson Prentice Hall.
Dweck, C. (1989). Motivation. In L. Lesgold, & R. Glaser, Foundations for a Psychological Education (pp. 87-136). Hillsdale, N J: Erlbaum.
Ericsson, K. A., Krampe, R. T., & Tesch-Romer, C. (1993). The role of deliberate practice in the acquisition of expert performance. Psychological Review , 100(3), 363-406.
Gick, M., & Holyoak, K. J. (1980). Analogical problem solving. Cognitive Psychology,12, 306-355.
Gick, M., & Holyoak, K. J. (1983). Schema induction and analogical transfer. Cognitive Psychology,15 , 1-38.
Hartzler, D. S. (2000). A meta-analysis of studies conducted on integrated curriculum programs and their effects on students achievement. Doctoral dissertation. Indiana University.
Hey, J., Linsey, J., Agogino, A. M., & Wood, K. L. (2008). Analogies and metaphors in creative design. International Journal of Engineering Education, 24 (2), 283-294.
Hmelo-Silver, C. (2004). Problem-based learning: What and how do students learn? Educational Psychology, 16 (3), 235-266.
Jeffers, A. T., Safferman, A. G., & Safferman, S. I. (2004). Understanding K–12 engineering outreach programs. Journal of Professional Issues in Engineering Education and Practice. 130 (2), 95-108. doi: 10.1061/~ASCE!1052-3928~2004!130:2~95!
Johnson, S. D. (1995). Transfer of learning. The Technology Teacher, 54 (7), 33-35.
Johnson, S. D. (1997). Learning technological concepts and developing intellectual skills. International Journal of Technology and Design Education, 7, 161-180.
Johnson, S. D., Dixon, R., Daugherty, J., & Lawanto, O. (2011). General versus specific intellectual competencies: The question of learning transfer. In M.Barak & M. Hacker (Eds.), Fostering Human Development through Engineering and Technology Education (pp. 55-74). Netherlands: Sense Publishers.
Kimbell, R., & Stables, K. (2008). Researching design learning: Issues and findings from two decades of research and development . Lexington, KY: Springer.
Lachapelle, C., & Cunningham, C. (2007). Engineering is elementary: Children's changing understandings of science and engineering. In Proceedings of the American Society for Engineering Education Annual Conference and Exposition . Honolulu, HI.
Lave, J. (1988). Cognition in Practice, New York, NY: Cambridge University Press.
Lewis, T. (2008). Creativity in technology education: Providing children with glimpses of their inventive potential. International Journal of Technology and Design Education, 19 (3), 255-258.
Mehalik, M. M., Doppelt, Y., & Schunn, C. D. (2008). Middle school science through design-based learning versus scripted inquiry: Better overall science concept learning and equity gap reduction. Journal of Engineering Education, 97 (1), 71-85.
National Research Council. (2000). How people learn: Brain, mind, experience and school. Washington, DC: National Academy Press.
Nathan, M. J., Tran, N., Phelps, L. A., & Prevost, A. (2008). The structure of high school academic and pre-engineering curricula: Mathematics. In Proceedings of the American Society of Engineering Education Annual Conference and Exposition. Pittsburgh, PA.
Needham, D. R., & Begg, I. M. (1991). Problem-oriented training promotes spontaneous analogical transfer: Memory-oriented training promotes memory for training. Memory and Cognition, 19 (6) 543–557.
Paivio, A. (1990). Mental representations. New York, NY: Oxford University Press.
Palinscar, A., & Brown, A. L. (1984). Reciprocal teaching of comprehension monitoring activities. Cognition and Instruction, 1, 117-175.
Perfetto, G. A., Bransford, J. D., & Franks, J. J. (1983). Contraints on access in a problem solving context. Memory and Cognition, 11, 24-31.
Project Lead the Way. (2012). Path way to Engineering: High school engineering program . Retrieved from http://www.pltw.org/our-programs/high-school-engineering-program .
Project Lead the Way. (2008). Introduction to engineering design: Analysis of cognitive levels of learning and mathematics and science content. Clifton Park, NY: Project Lead the Way Inc.
Sanders, M. (2009). STEM, STEM education, STEM mania. The Technology Teacher, 68 (4), 20-26.
Schunn, C.D., & Silk, E. M. (2011). Learning theories for engineering and technology education. In M. Barak & M. Hacker (Eds.). Fostering Human Development through Engineering and Technology Education (pp. 55-74). Netherlands: Sense Publishers.
Singley, A., & Anderson, J. R. (1989). The transfer of cognitive skill . Cambridge, M A: Harvard University Press.
Spiro, R. J., Feltovitch, P. L., Jackson, M. L., & Coulton, R. L. (1991). Cognitive flexibility, constructivism, and hypertext: Random access instruction for advanced knowledge acquisition in ill-structured domain. Educational Technology 31 (5), 24-33.
Spiro, R. J., Vispoel, W. P., Schmitz, J. P., Samarapungavan, A., & Boerger, A. E. (1987). Knowledge acquisition for application: Cognitive flexibility and transfer in complex domains. (ERIC Document Reproduction Service No. ED 287 155).
Sutton, M. J. (2003). Problem representation, understanding, and learning transfer: Implications for technology education research. Journal of Industrial Teacher Education, 40 (4) , 47-61.
Tran, N., & Nathan, M. (2010). Pre-college engineering studies: An Investigation of the relationship between pre-college engineering studies and student achievement in science and mathematics. Journal of Engineering Education, 92 (2), 143-157.