Examining Students' Proportional Reasoning Strategy Levels as Evidence of the Impact of an Integrated LEGO Robotics and Mathematics Learning Experience
Examining Students' Proportional Reasoning Strategy Levels as Evidence of the Impact of an Integrated LEGO Robotics and Mathematics Learning Experience
In many school districts in the United States, the Common Core State Standards for Mathematics ( National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010 ) outline what students should understand and be able to do in their study of mathematics. These standards are composed of content standards and practice standards that must be connected in order to allow students to engage more deeply with the subject matter. Engagement and learning in context can support understanding in a couple of ways. The first is by increasing student motivation and interest in the curriculum itself. The second is by enhancing transfer of learning through the demonstration of connections between abstract mathematics and real-world problems. Students must be prepared to apply this knowledge in multiple external situations, often through creative and personally meaningful situations, as well as to learn to address mathematical problems in a variety of situations and contexts.
The presented study used a problem-solving experience in engineering design with LEGO robotics materials as the real-world mathematics-learning context. The goals of the study were (a) to determine if a short but intensive extracurricular learning experience would lead to significant student learning of a particular academic topic and (b) to explore the differences in mathematical problem-solving strategies used by students when solving problems of ratio and proportion in two different learning environments. It was important to first determine if indeed a short-term but intensive extracurricular learning experience could be effective, given the reliance of such an experience as the framework for conducting the educational research. The experimental research explored student learning in mathematics but deliberately limited the specific topic of exploration to integrated concepts of proportional reasoning within LEGO robotics challenges in engineering design. The impact of this experience upon students' proportional reasoning was measured and is described with a focus on proportional reasoning strategy levels.
Two research questions guided this study:
- Research Question 1: Can a significant change in students' understanding of ratio and proportion take place during a short but intense learning experience?
- Research Question 2: How do students' demonstrated proportional reasoning strategy level use compare for students learning ratio and proportion concepts within the integrated LEGO robotics and mathematics program versus when using a traditional textbook-based mathematics program?
Literature Review
LEGO Robotics in K-12 Engineering
Research exploring the cognitive impact of engineering education at the kindergarten through twelfth grade level (K-12 engineering) suggests that such learning experiences can build creative design skills and foster the utilization of higher order thinking and problem solving skills ( Amsel, Goodman, Savoi, & Clark, 1996 ; Foster & Wright, 2001 ; Roden, 1995 ). Furthermore, K-12 engineering can serve as a vehicle to effectively integrate and teach across content areas ( Barlex & Pitt, 2000 ; Cross, 2007 ; Martínez Ortiz, 2004 ; Moundridou & Kaniglonou, 2008 ). There are longstanding debates across STEM education about whether the T (technology content) and the E (engineering content) should be stand-alone K-12 subjects or integrative activities ( Katehi, Pearson, & Feder, 2009 ; U.S. Department of Education National Assessment Governing Board, 2014 ). The merits of the stand-alone approach are that engineering and technology would be given the spotlight and focus paralleling their importance in the educational and workplace landscape allowing clear career connections to be made. However, the major challenge still lies in the difficulty of finding time during the school day to dedicate to these additional content areas. Therefore, in this study, the integrative approach was explored. In this study, K-12 engineering was utilized as a curricular framework for the integrated exploration of proportional reasoning concepts. In addition, the use of robotics allowed opportunities and specific problem solving contexts for the teaching and learning of ratio and proportion. K-12 engineering, with an emphasis on technology, can serve as a platform for providing inquiry-based learning with real-world contexts and collaborative problem solving.
The design of this study was motivated by the work of Papert (1980) , who pioneered and investigated how technology could be used to help children learn mathematics differently. He developed a philosophical approach called constructionism and a supporting programming language called Logic Oriented Graphic Oriented (LOGO) language. Massachusetts Institute of Technology researchers then collaborated with the LEGO® Company to design a control unit (the brick) embedded with computational power that could accommodate the mounting of traditional LEGO blocks to design and build controllable LEGO construction projects. This control brick, known as a Mindstorms RCX, runs basic programs written by students using a simple graphical interface on a personal computer. Together, the LEGO blocks and the programmable brick can empower children with the capability to design and interact with the physical world through their own insight and programming determination. The LEGO blocks can be used in a collaborative design environment that allow for team design and variable setting that is further facilitated by the additional controllable options such as motor settings, use of add-on sensors, and infrared communication devices ( Resnick, Martin, Sargent, & Silverman, 1996 ). Several generations of this tool have followed the original LEGO Mindstorms RCX; however, due to cost and material limitations at the school district level, the original version was used in this study.
Integrated Engineering and Mathematics
This study is based on the proposition that engineering robotics can be integrated with mathematics and serve as a context to offer students the opportunity for improving their proportional reasoning. The hypothesis is that learning in the context of engineering robotics may be more meaningful and long lasting for students than learning with a non-engineering, textbook-based mathematics curriculum ( Martínez Ortiz, 2008 ). The interconnected concepts of multiplication, division, fraction, ratio, and rational numbers often appear in problem situations that students encounter in real-world experiences. These concepts are also related mathematically to such an extent that when taken all together, they may define a unique mathematical conceptual field. Vergnaud (1983) calls this the multiplicative conceptual field (MCF) and defines it as "a set of problems and situations for the treatment of which concepts, procedures, and representations of different but narrowly interconnected types are necessary" (p. 127). Vergnaud suggests that the MCF includes concepts in multiplication and division, linear and bilinear functions, dimensional analysis, linear mapping, and linear combinations of magnitudes as well as ratio, rate, fraction, and rational numbers. He maintains that these mathematical concepts do not exist in isolation but rather in a network of conceptual relations and problem situations. Similarly, student mathematical reasoning develops and is called upon to consider various mathematical problem-solving situations.
The Role that Contexts Play in Assessment Problems in Mathematics
Using the terminology of Chevallard (1990, 2007) , the assessment instruments used in this study were designed in order to allow for the determination of the influence of the context of the assessment task on students' performance. The intra-mathematical problems or pure mathematical questions utilized only numbers and letters. Alternately, extra-mathematical questions appeared to the student in contexts outside of pure mathematics. The definition for context in this case provided by Borasi (1986) is appropriate: "a characteristic of a task presented to the students: referring either to the words and pictures that help the students to understand the task, or concerning the situation or event in which the task is situated" (p. 129). Results from this study showed that after instruction, students performed better on the extra-mathematical assessment as compared to the intra-mathematical questions. This suggests that extra-mathematical contexts in mathematics assessment can offer the students more opportunity for demonstrating their abilities due to the opportunity for sense making that these contexts provide and the multiple approaches that students can take to solve the problem when presented along with extra-mathematical contexts. In contrast, an intra-mathematical problem generally relies on a specific operation to be performed and is therefore limiting in that it does not provide the opportunity for students to focus on making sense of the situation, whereas a contextually based problem might otherwise contribute to this sense making. These observations are supported by the work of many researchers in mathematics education such as Carraher, Carraher, and Schliemann (1985) , Carpenter and Moser (1984) and Clements and Sarama (2007) .
Proportional Reasoning Research
Research on proportional reasoning at the elementary school level ( Tourniaire, 1986 ) has shown that children in Grades 3, 4, and 5 may demonstrate a grasp of the concept of proportion, but it begins as a fragmented ability that relies on the context of the problem. There remain gaps in the research in regards to the most effective methods for teaching proportional reasoning. Some evidence suggests that simply structured ratio and proportion problems that utilize small numbers and integer ratios are within the grasp of the elementary school child and that when coupled with appropriate manipulatives, high quality teaching and critical thinking-based curricula can improve student understanding of ratio and proportion ( Karplus, Pulos, & Stage, 1983 ; Tourniaire, 1986 ).
Proportional reasoning is a kind of mathematical reasoning that students use when solving problems in the multiplicative conceptual field. Research indicates that the ability to reason proportionally is important for students' mathematical development and is essential for learning advanced topics in mathematics ( Behr, Harel, Lesh & Post, 1987 ; Kaput & West, 1994 ). However, there is also evidence that students perform better when "encouraged to construct their own . . . knowledge . . . through collaborative problem solving activities" involving proportion than when they participate more passively in "more traditional, teacher-directed instructional experiences" ( Ben-Chaim, Fey, Fitzgerald, Benedetto & Miller, 1998 , p. 247). Proportional reasoning is important to this study because the engineering robotics context includes collaborative problem-solving activities that directly call upon the use of proportional reasoning. Proportional reasoning calls upon the understanding and application of skills within the MCF to make sense of mathematical relationships using ratios and equations involving ratios. Mathematical problems of ratio and proportion can be analyzed by using the concepts of multiplication, division, fractions, and linear functions. Proportional reasoning involves the understanding of the relationship of two numbers (ratio) as the critical multiplicative comparator. Researchers propose that although proportional reasoning does not appear to be an automatically developed concept, students do encounter many opportunities for developing proportional reasoning in their daily lives as well as in the elementary and middle school classroom ( Karplus, Pulos, & Stage, 1983 ; Lamon, 1993 ). Harel, Behr, Post, and Lesh (1987) have called proportional reasoning a watershed concept, a cornerstone of higher mathematics and the capstone of elementary concepts.
Methods
This study examined the impact of using LEGO robotics engineering in support of students' learning of ratios and proportion in intra-mathematical contexts, various extra-mathematical contexts not involving engineering (word problems not involving hands-on engineering design), and extra-mathematical contexts involving engineering. The study utilized an experimental mixed-methods repeated-measures design with a small sample of students (n = 30) in which one group of students (n = 15) participated in each treatment condition. Student participants applied for a 1-week mathematics program and were assigned to either the intervention group or the comparison group, therefore allowing internal validity for group result comparisons. There were two conditions included in this study: The first condition was the learning of ratios and proportions in a non-engineering textbook-based mathematics intervention program (i.e., the control group), and the second condition was the learning of ratio and proportion in an integrated engineering and mathematics intervention program (i.e., the experimental group). The repeated measures design was intended to compare students' understanding of ratio and proportion between experimental and control-group students after a weeklong intervention program. Each student was assessed at three different time points. Measures were collected at the beginning (T1) and end (T2) of each intervention program, and an additional measure was collected 10 weeks after the intervention programs (T3), as shown in Figure 1.
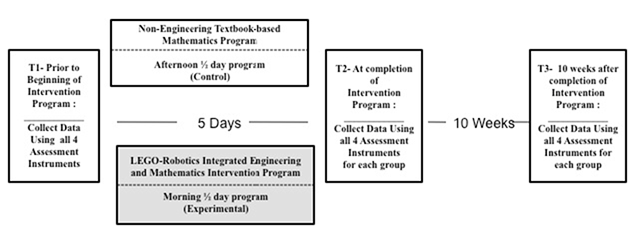
Figure 1. Experimental design with control group and repeated measures.
Intervention Program Cirricula
In the state of Texas, the Texas Education Agency (TEA) directs the state learning frameworks for K-12 students in the state of Texas by defining specific content standards. These standards are known as the Texas Essential Knowledge Standards (TEKS). Towards the end of fifth grade, the mathematics TEKS begin introducing concepts of ratio and proportion in preparation for sixth grade, a year of focus upon proportional reasoning development ( Texas Education Agency, 2008 ). For this reason, this study included fifth grade students and offered unique extracurricular learning programs guided by sixth grade TEKS in each program: a non-engineering textbook-based intervention program and a LEGO-based engineering robotics program.
LEGO-based Engineering Robotics Program. The goal of the LEGO-based engineering robotics program was to teach ratio and proportion using theory-based principles within an engineering design context in a small group peer-learning environment. One major curricular component of the engineering design context was the engineering design process. The eight-step engineering design process defined within the Massachusetts state standards ( Massachusetts Department of Education, 2001 ) is a robust model for teaching engineering design concepts to students. However, the eight steps require substantial explanation and practice and may be a more appropriate model to use with older students and certainly in a longer duration learning opportunity that offers more time for focus on each of the eight steps of the engineering design process. A simple four step engineering production improvement model called the Plan, Do, Check, Act Cycle (Deming, 1986; Shewhart, 1986) was modified as Plan, Build, Check, Improve (PBCI), as shown in Figure 2, and was shared with the students in the engineering intervention program. This four-Step Engineering Design Process model (named Fusion by the author) was therefore selected over others models ( Museum of Science, n.d.; Puntambeker, 2005 ), to include in the curriculum of the engineering intervention program.
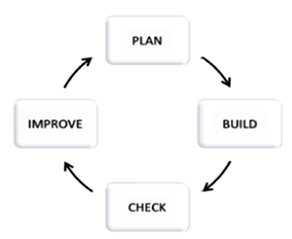
Figure 2. The four-step Fusion engineering design process model.
Students were encouraged to approach their mathematics problem solving and design challenges using the systematic nature of the engineering design process as well as the feedback data and support skills emphasized in this process (e.g., use of symbols and sketches, systemic testing of variables, use of graphic organizers). The program instructor encouraged students to learn and use this approach by introducing the engineering design process, by posting a graphic of it in the classroom, by modeling and providing mathematics problem solving examples using the engineering design process, and by providing worksheets with prompting questions and a graphic organizer that integrated this process. In addition to this process standard, five additional learning objectives, unique to the LEGO robotics engineering program, were defined in order to clearly guide in the teaching of this program. Although the experimental program students participated in the same number of instruction hours as the control group, their instructional program addressed mathematics and engineering content as guided by mathematics TEKS and research-based standards for elementary engineering learning from the Massachusetts state standards ( Massachusetts Department of Education, 2001 ). The Massachusetts standards for elementary engineering were used because at the time, Texas did not have adopted state standards for engineering learning at the elementary level. In addition, the experimental program curriculum used in this study was developed as a modified curriculum that was previously utilized in an elementary engineering and mathematics integrated teaching program with LEGO robotics developed by the author ( Martínez Ortiz, 2005 ).
Experimental Group. The experimental group consisted of 15 fifth grade students from a low income inner-city elementary school in Austin, Texas. This group participated in a weeklong integrated engineering and mathematics intervention program (titled "Engineering Fusion") through which they received an engineering robotics curriculum that integrated LEGO robotics and mathematics instruction in ratio and proportion. The program was delivered as a five-session program totaling 15 instructional hours, supported by one teacher as instructor along with one teacher aid. Both teachers were school campus teachers, but not regular fifth-grade classroom teachers. The principal teacher for both intervention programs was an experienced mathematics specialist teacher whose usual role included providing some classroom mathematics lessons, so she and the students were familiar with each other. The teacher aid was a campus afterschool instructor who was knowledgeable in the use of LEGO robotics and was also familiar with the school and with some of the students.
Non-engineering Textbook-based Intervention Program. A non-engineering textbook-based curriculum is the accepted pedagogical approach for teaching students the mathematics TEKS in most Texas school districts. In the textbook-based intervention program (or control) program, the daily lessons were designed by selecting material from the district-adopted fifth-grade mathematics resource book. This material is usually provided as an optional set of lesson plans because it addresses sixth grade TEKS for ratio and proportion at the end of the fifth grade. The sixth-grade TEKS were used because ratio and proportion learning expectations do not formally appear until the sixth grade. This also allowed for greater confidence in the assertion that program students had not received prior instruction in the topic. In the control condition, students received five 3-hour sessions of textbook mathematics lessons on ratio and proportion to address four major mathematics TEKS regarding proportional reasoning. These included specific TEKS for sixth grade from the strand of mathematical concepts labeled as "number, operation, and quantitative reasoning" ( Texas Education Agency, 2008 ). This strand of mathematical concepts describes the knowledge expectation that students use and represent rational numbers in a variety of equivalent forms. In addition, TEKS for sixth grade from the strand of mathematical concepts labeled as "patterns, relationships, and algebraic thinking" ( Texas Education Agency, 2008 ) were included in which students were expected to solve problems involving proportional relationships, specifically representing and using rational numbers in a variety of equivalent forms. Students also had extended opportunities to work with non-engineering mathematics manipulatives (such as Cuisenaire rods) and to carry out mathematics worksheet practices.
Control Group. A second group of 15 fifth grade students from the same low income inner-city elementary school in Austin, Texas participated as the control group. Control students participated in a 15-hour non-engineering mathematics intervention program through which they received mathematics instruction in ratio and proportion based on the school district adopted textbook. This program was also delivered as a five-session program totaling 15 hours, supported by the same principal teacher and teacher aid as in the experimental group. Non-engineering mathematics refers to the pedagogical approach of one classroom of students learning in a classroom directed by one teacher providing a textbook-based lecture with worksheet practice and some use of manipulatives.
Assessment Instruments: Computational vs. In-Context
Data were collected to assess the students' proportional reasoning strategy levels demonstrated in solving each of the assessment problems selected to assess the learning of students in each of these intervention programs. The contexts were three- computational (paper and pencil) proportional reasoning, general contexts, and engineering design contexts using each of the three assessment instruments shown in Table 1: (a) Intra-Prop assessment, (b) Extra-Prop assessment, and (c) Engin-Prop assessment.
| Instrument | Context | Scoring for Proportional Reasoning Strategy Level |
|---|---|---|
| Intra-Prop | Measures the understanding of ratio and proportion concepts by numerical computation problem solving [only included number sentences]. | Included 10 questions. Each student answer sheet was reviewed and assigned a numeric level assessment score (0, 1, 2, or 3) to each question using the Langrall and Swafford modified scale (described in the following section). The total score = mean score. |
| Extra-Prop | Measures the understanding of ratio and proportion in general-context mathematical word problems. | Included 10 questions. Each student answer sheet was reviewed and assigned a numeric level assessment score (0, 1, 2, or 3) to each question using the Langrall and Swafford modified scale (described in the following section). The total score = mean score. |
| Engin-Prop | Measures the understanding of ratio and proportion in a LEGO engineering problem solving context. | Included 8 questions. Each student answer sheet was reviewed and assigned a numeric level assessment score (0, 1, 2, or 3) to each question using the Langrall and Swafford modified scale (described in the following section). The total score = mean score. |
The instruments, specifically designed for this study, were administered to capture background information, measure students' basic understanding of some engineering and mathematics definitions, and to measure students' understanding of ratio and proportion. The understanding of ratio and proportion through numerical computation was measured using the Intra-Mathematical Proportional Reasoning Test (Intra-Prop). The understanding of ratio and proportion in general-context mathematical word problems was measured using the Extra-Mathematical Proportional Reasoning Test in a General Context (Extra-Prop). The understanding of ratio and proportion in a LEGO engineering context was measured using a mathematical tool called the Extra-Mathematical Proportional Reasoning Test in an Engineering Context (Engin-Prop).
Assessment of Proportional Reasoning: Selection of a Scale . Although there is a wealth of research on the development of children's proportional reasoning ( Hart, 1984 ; Kaput & West, 1994 , Lamon, 1994 ; Harel, Behr, Post, & Lesh, 1987 ), there is much less focus on the development of diagnostic instruments for assessment of proportional reasoning. A few diagnostic instruments and/or assessment guidelines ( Baxter & Junker, 2001 ; Langrall & Swafford, 2000 ; Misailidou & Williams, 2003 ) were reviewed to determine if their research-based scales or guidelines might support the data analysis of student proportional reasoning strategy levels for this study. These were found to be qualitatively similar to each other (level to level), and all three were based on similar bodies of established developmental proportional reasoning research. Langrall and Swafford (2000) proposed a proportional reasoning scale. They classified the strategies that students use in proportional reasoning into four different levels: levels 0, 1, 2, and 3. Level 0 students do not display any proportional reasoning at all. Level 1 students do not use proportional reasoning strategies yet may arrive at the correct answer by relying on qualitative strategies using pictures, models, or manipulatives to help solve proportional problems. Level 2 students begin to use numeric strategies such as the simple additive strategy as well as build-up scalar strategies that employ multiplication and division. Level 3 students show formalized proportional thinking using functional strategies and use of ratio variable comparison and manipulation. This scale was consistent with the research base reviewed and the focus on younger students, such as the 10-11 year olds in this study. This scale was therefore selected for the interpretation of students' strategic thinking and the coding of the data collected using the ratio and proportion instruments discussed.
In addition, a repeated-measures design was used to compare the mathematics achievement in proportional reasoning of intervention students over a longitudinal period of a school trimester. Descriptive statistics and ANOVA statistics were utilized to determine if there were any significant differences in the performance of these two groups. Students in the engineering LEGO Fusion program received instruction in mathematics, an overview of the engineering design process, and instruction regarding building and programming with LEGO robotics. The programming instruction was pared down to a limited introduction using a visual programming language. Robolab was used as the graphical programming language because that was available to students for future use. Student were provided design challenges that allowed them to consider the robots' physical environment, control basic functions and variables through structural design, and programming and evaluating the performance of their robots by utilizing mathematical understanding and skills of measuring and comparing variable relationships.
| Level | Strategies Exhibited | Author Selected Student Example of the Proportional Reasoning Level |
|---|---|---|
| Level 0: Non-proportional reasoning |
"Guesses or uses visual clues . . .
Is unable to recognize multiplicative relationships Randomly uses numbers, operations or strategies Is unable to link the two measures" (Langrall & Swafford, 2000). Does not lead to correct solutions or development of more mature proportional reasoning |
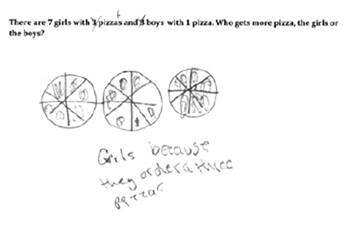
|
| Level 1: Informal reasoning about proportional situations |
"Uses pictures, models, or manipulatives to make sense of situations
Makes qualitative comparisons" (Langrall & Swafford, 2000). |
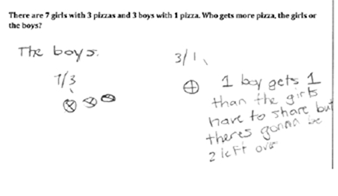
|
| Level 2: Quantitative reasoning |
"Unitizes or uses composite units
Finds and uses unit rate Identifies or uses scalar factor or table Uses equivalent fractions Builds up both measures" (Langrall & Swafford, 2000). Uses scalar strategies |
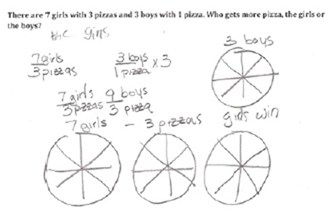
|
| Level 3: Formal proportional reasoning |
"Sets up proportion using variables and solves using cross-product rule or equivalent fractions
Fully understands the invariant and covariant relationships" (Langrall & Swafford, 2000). Displays functional reasoning |

|
Results
The research questions were addressed by analyzing the quantitative results of both groups of students (engineering based and non-engineering based) and their changes in correct responses to proportional reasoning questions set in different contexts as well as ratings of the level of proportional reasoning strategies used at each of the three time points. The scale used to assign a score for proportional reasoning level to each student's work was Langrall and Swafford's (2000) scale, which was discussed in the previous section, with possible scores of 0, 1, 2, and 3. Each item in the student's assessment was assigned a single proportional reasoning score, a mean was calculated for each student's assessment, and then a mean was derived for the 15 students' scores from each group. Each of the three assessments was scored first for percentage of correct answers and second for mean level of proportional reasoning using the Langrall and Swafford scale. The assessment instruments included the same questions when scored for percentage correct, as when scored for mean level of proportional reasoning. In the following sections, the assessment results that were used in the analysis of variance (ANOVA) runs were the level of proportional reasoning strategy-use results for each of the three assessments: the Intra-Prop, Extra-Prop, and Engin-Prop.
Proportional Reasoning Levels Analysis: Intra-Prop
Table 3 shows the descriptive statistics for each program group's performance on the Intra-Prop at each of the three time points. Figure 3 displays the mean level of strategy-use scores (0-3) on intra-prop for program groups across three time points.
| Time of Intra-Prop Assessment | Program Group | Mean | SD | N |
|---|---|---|---|---|
| T1 | Control Group | .27 | .458 | 15 |
| Experimental Group | .47 | .516 | 15 | |
| Total | .37 | .49 | 30 | |
| T2 | Control Group | .67 | .617 | 15 |
| Experimental Group | .67 | .617 | 15 | |
| Total | .67 | .606 | 30 | |
| T3 | Control Group | .87 | .640 | 15 |
| Experimental Group | .80 | .516 | 15 | |
| Total | .83 | .592 | 30 |
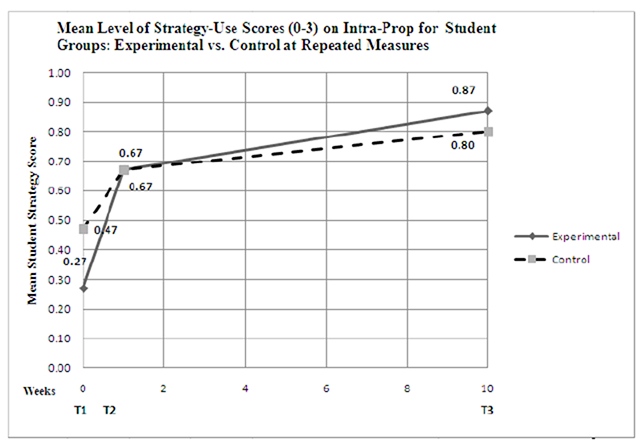
Figure 3. Mean level of strategy-use scores (0-3) on intra-prop for program groups across three time points.
The experimental group's mean score was .27 at T1. This implies that the majority of students were closer to Level 0 of proportional reasoning at T1. This same group of students achieved a .67 mean score immediately after the conclusion of the intervention program. This implies that the majority of the students were closer to Level 1 of proportional reasoning. At this level, proportional reasoning strategies are not yet clearly used, but students rely on qualitative strategies such as the use of pictures, and they are able to use some multiplicative thinking to arrive at the correct answer. At T3, the use of proportional reasoning strategies increased even more, to the level of .87. Although students show an increase in use of statistical reasoning at the 10-week post-post assessment, the scale score only defines integer values, so the changes at each time point are all still within the zero (0) score of the scale, meaning that students were not judged to have demonstrated proportional thinking.
A mixed between-within subjects ANOVA was conducted to assess the impact of the two different interventions (non-engineering textbook-based mathematics intervention program versus LEGO robotics integrated engineering and mathematics intervention program) based on the level of proportional reasoning strategies used by the participants, as reflected by their level of strategy-use scores on the Intra-Prop at T1, T2, and T3. There was no significant interaction between program type and time, Wilks' Lambda = .951, F(2,27) = .690, p = .510, partial eta squared = .049. There was a substantial main effect for time, Wilks' Lambda = .625, F(2,27) = 8.114, p = .002, partial eta squared = .375, with both groups showing an increase in the level of proportional reasoning strategies used, as measured by their overall level of strategy-use scores on the Intra-Prop. The main effect comparing the two types of intervention was not significant, F(1,28) = .07, p = .791, partial eta squared = .002, suggesting no difference in the effectiveness of the two teaching approaches when measured by the level of strategy-use score on the Intra-Prop. The control group's mean score on the Intra-Prop was stronger (.47) than the experimental group (.27) at T1. However, this score is somewhat deceptive because the strategic reasoning scores assigned to each problem were integer values of 0, 1, 2, and 3; at the levels reported, both groups were determined to be at between 0 (non-proportional reasoning) and 1 (informal reasoning about proportional situations). After the intervention, both groups improved with the levels becoming a lot more similar (.67) but still under Level 1. This indicates that students learned to use slightly higher levels of proportional reasoning strategies. It could also mean that the types of problems presented did not require these students to use higher level strategies and that given the straightforward intra-mathematical nature of the assessment, students were equally prepared to solve the problems regardless of their learning experience.
Proportional Reasoning Levels Analysis: Extra-Prop
Table 4 shows the descriptive statistics for each program group's performance on the Extra-Prop at each of the three time points. Figure 4 displays the mean score for strategy level use on the Extra-Prop assessment by each group (experimental and control) at each of the three time points.
| Time of Extra-Prop Assessment | Program Group | Mean | SD | N |
|---|---|---|---|---|
| T1 | Control Group | 1.20 | .941 | 15 |
| Experimental Group | 1.27 | .704 | 15 | |
| Total | 1.23 | .817 | 30 | |
| T2 | Control Group | 2.13 | .640 | 15 |
| Experimental Group | 2.47 | .516 | 15 | |
| Total | 2.30 | .596 | 30 | |
| T3 | Control Group | 2.13 | .640 | 15 |
| Experimental Group | 2.47 | .516 | 15 | |
| Total | 2.30 | .596 | 30 |
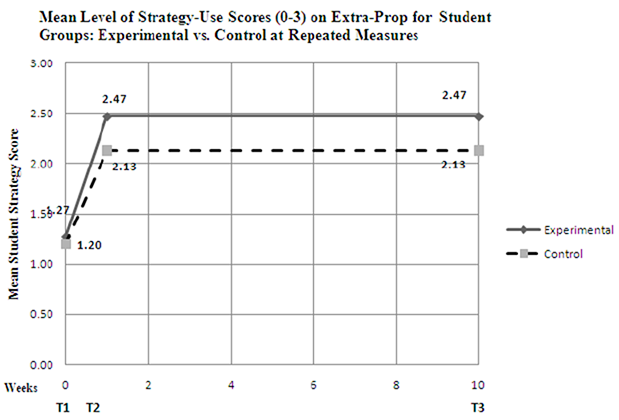
Figure 4. Mean strategy level scores (0-3) on extra-prop for program groups across three time points.
There is an indication of students' improvement from an average of Level 1 of proportional reasoning strategies demonstrated to an average of Level 2 of proportional reasoning strategies. However, both groups changed similarly, regardless of the teaching approach they were exposed to. Level 2 is quantitative, and perhaps their prior school experiences had reinforced quantitative and algorithmic strategies over higher level reasoning strategies. Level 2 proportional reasoning allowed them to achieve a relatively high percentage of correct answers (experimental mean score = 77.3%; control group mean score = 62%), so they did not need to go further. As seen in Figure 3 above, student mean strategy levels for both groups do not drop after 10 weeks. Perhaps this indicates that students in both intervention groups have learned to apply quantitative proportional reasoning strategies (at an average level of 2) and they retain this knowledge over time. This is an important accomplishment that might not have been apparent if only measured by the percentage correct score on the same test at T3. Student work displays their use of proportional reasoning strategies, even though their final answer may be incorrect. A mixed between-within subjects ANOVA was conducted to assess the impact of two different interventions (non-engineering textbook-based mathematics intervention program and LEGO robotics integrated engineering and mathematics intervention program), based on the level of proportional reasoning strategies used by the participants as reflected by their level of strategy-use scores on the Extra-Prop at T1, T2, and T3. There was no significant interaction between program type and time, Wilks' Lambda = .973, F (2, 27) = .772, p = .387, partial eta squared = .027. There was a substantial main effect for time, Wilks' Lambda = .362, F(2,27) = 49.434, p = .000, partial eta squared = .638, with both groups showing a large increase in the level of proportional reasoning strategies used, as measured by their overall level of strategy-use scores on the Extra-Prop. The main effect comparing the two types of intervention was not significant, F (1, 28) = .1.483, p = .233, partial eta squared = .050, suggesting no difference in the effectiveness of the two teaching approaches when measured by the level of strategy-use score on the Extra-Prop.
Proportional Reasoning Levels Analysis: Engin-Prop
Table 5 shows the descriptive statistics for each program group's performance on the Extra-Prop at each of the three time points. Figure 5 displays the mean score for strategy level use on the Engin-Prop assessment by each group (experimental and control) at each of the three time points.
| Time of Engin-Prop Assessment | Program Group | Mean | SD | N |
|---|---|---|---|---|
| T1 | Control Group | 1.07 | .704 | 15 |
| Experimental Group | 1.13 | .640 | 15 | |
| Total | 1.10 | .662 | 30 | |
| T2 | Control Group | 1.00 | .655 | 15 |
| Experimental Group | 2.47 | .516 | 15 | |
| Total | 1.73 | .944 | 30 | |
| T3 | Control Group | .87 | .640 | 15 |
| Experimental Group | 2.40 | .507 | 15 | |
| Total | 1.63 | .964 | 30 |
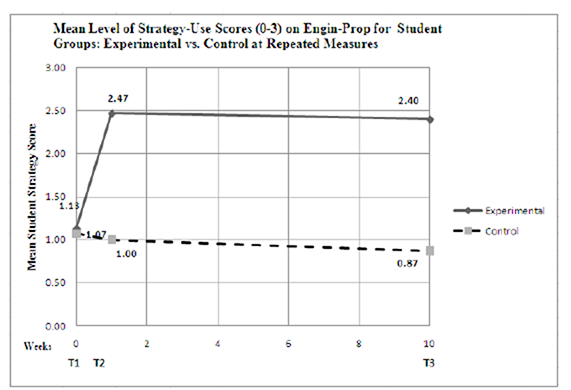
Figure 5. Mean strategy level scores (0-3) on engin-prop for program groups across three time points.
The range of the proportional reasoning score for the Engin-Prop assessment was 0-3. The mean strategy score for the 15 students in the experimental group began with a strategy score of 1.13. Students achieved a score of 2.47 at T2 and 2.40 at T3. The data for the control students are shown as a benchmark. However, it is not expected that students would demonstrate any change because control group students did not receive instruction in the use of LEGO robotics. It is noteworthy, nonetheless, that the accomplishments of the experimental group were achieved within the same overall program instructional time as that of the control group.
A mixed between-within subjects ANOVA was conducted to assess the impact of two different interventions (non-engineering textbook-based mathematics and LEGO robotics integrated engineering and mathematics) based on the level of proportional reasoning strategies used by the participants as reflected by their level of strategy-use scores on the Engin-Prop at T1, T2, and T3. In this case, there was significant interaction between program type and time, Wilks' Lambda = .419, F(2,27) = 18.684, p = .000, partial eta squared = .581. There was also a substantial main effect for time for the experimental group, Wilks' Lambda = .502, F(2,27) = 13.377, p = .000, partial eta squared = .498, with the experimental group showing an increase in the level of proportional reasoning strategies used, as measured by their overall level of strategy-use scores on the Engin-Prop. The main effect comparing the two types of intervention was significant, F(1,28) = .31.381, p = .000, partial eta squared = .528, suggesting a significant difference in the effectiveness of the two teaching approaches when measured by the Engin-Prop. This main effect was to be expected given that the Engin-Prop included many items that were better understood by students that had actually received instruction in engineering LEGO robotics as well as ratio and proportion mathematics.
Discussion
This study was designed to determine the possible impact of an integrated engineering and mathematics teaching approach using LEGO robotics upon students' learning of concepts of ratio and proportion. The results of this study indicated that the students were able to make significant progress in learning new concepts of ratio and proportion while also learning basic definitions related to LEGO robotics engineering design and programming when this learning took place in an integrated engineering and mathematics context. It has been shown that a statistically significant change in students' understanding of ratio and proportion took place during the relatively short but intense learning experience, regardless of the type of intervention to which the students had been exposed. Even students who were exposed to a traditional textbook curriculum experienced changes in their scores. This confirms that the 3 hours of instruction daily in a 5-day program during a normal planned school-year break (that included no other schoolwork) allowed students to focus on and learn about the academic topics taught. These students were motivated to attend a program that was advertised to be of an academic nature, so perhaps they were intrinsically motivated to learn. However, the more important finding is that the 15 hours of focused instruction with quality curricula (textbook-based and non-textbook-based) was sufficient to allow students to significantly increase the number of correct responses to problems of ratio and proportion.
The performance of students in the experimental group on the Intra-Prop was not significantly higher than that of the performance of students in the control group. This might indicate that students that are taught concepts of ratio and proportion in a focused intervention program will learn how to solve problems of ratio and proportion in intra-mathematical contexts just as well, regardless of the differences in instructional methodology and with or without engineering integrated into their learning experience. The performance of students in the experimental group on the Extra-Prop was significantly higher than the performance of students in the control group. These results indicate that students that learn about ratio and proportion in an engineering-related context improve in their understanding significantly and retain their learning for a longer period of time when they encounter these situations in an extra-mathematical context versus in an intra-mathematical context.
The performance of students in the experimental group on the Engin-Prop was significantly different than the performance of students in the control group. However, even these students did not use particularly high levels of proportional reasoning strategies. It may be unrealistic to expect students to achieve higher levels of proportional reasoning in such a short intervention program. In addition, the young students in this class seemed to be more comfortable with solving problems as simply as possible and were able to "get the right answer" with only Level 2 proportional reasoning strategies.
The main message of these findings is that educational robotics can serve as a motivating context that may be very beneficial as an instructional tool in the integrated engineering mathematics classroom when teaching concepts of ratio and proportion and potentially many others. It is important and productive for students to be allowed the opportunity to learn mathematics concepts accompanied with meaningful constructionist experiences such as those provided by LEGO educational robotics in an integrated engineering and mathematics design setting. Perhaps these experiences influence the level of engagement and thoughtful approaches that lead to deeper student understanding of mathematics concepts-in this case, ratio and proportion concepts. One finding of special note to practitioners is the fact that students in the experimental group were able to learn at least as much and as well (if not more) of the mathematics content topic of ratio and proportion as compared to the control group of students. Additionally, within the same amount of time, experimental group students learned and retained engineering and related applied ratio and proportion mathematics concepts.
Limitations of the Study and Future Research
The experimental intervention program described in this study was a program that integrated engineering design and educational robotics application opportunities in addition to the same mathematics objectives regarding ratio and proportion as the non-engineering mathematics intervention program. The intervention and control programs took place in the same school setting as extracurricular programs occurring during a holiday week when school was not in session. The experimental program took place in the morning, and the control program took place in the afternoon. This introduced a variable (learning in the morning versus learning in the afternoon) that was beyond the control of this study and is certainly a limitation. The study was designed and carried out in spite of this limitation in order to maintain the same instructor for both student groups. Although morning versus afternoon course time is a factor that may certainly have affected the performance of the students, introducing a different instructor may have introduced much greater variability.
Another limitation of this study was that only one student group received the opportunity to learn about LEGO robotics and use LEGO robotics in engineering design challenges requiring mathematical thinking. Although this was precisely the intent of the study in order to compare the impact of the two differing learning experiences, it limited the ability of comparison of learning in the engineering context between the two groups. In this study, it is not appropriate to compare learning differences of LEGO engineering concepts between the two groups because one group was not exposed to LEGO engineering concepts. However, the analysis presented in this study does show a comparison only as a benchmark as to how much students might already know about LEGO engineering concepts without explicit instruction. Given the low socioeconomic status of both student groups, it is not likely that students have access to expensive LEGO robotics materials at home or at school.
Another limitation of this study was the short duration of the learning experience. This limitation was driven by the interest in controlling the mathematics learning levels of the participating students. Because students were in different classrooms and in different households, the mathematics learning experiences that each might be exposed to would increase as the time increased. However, as was shown, all had a significant change in their learning of the proportional reasoning concepts expected. This supported that even a short duration learning experience, if purposefully designed and intense, can support significant and sustained student learning.
This research study focused primarily on students, and the author sought to measure student mathematical learning and skill development. In order to capture detailed qualitative data, the overall sample size of n = 30 was small, which limited the power of statistical analysis and generalization of results. Although there was pretesting (P1) conducted for all students, a more in-depth analysis could be conducted using the P1 scores as a covariate to describe the differences between the groups. Future studies can be repeated with the support of additional research and instructional support that will allow for a larger number of participants. External validity can be addressed by repeating this study at multiple schools, both with similar and differing student demographics. Finally, in light of the conclusions regarding the positive impact of the integrated content teaching approach for mathematics and engineering using LEGO robotics, a future direction would be to analyze the specific techniques that expert teachers utilize to effectively teach integrated content, specifically when working with educational robotics and mathematics. Such research would help to better identify the pedagogical skills and content knowledge necessary to teach well in such a setting.
Araceli Martínez Ortiz ( araceli@txstate.edu ) is Director of the LBJ Institute for STEM Education & Research, and is a Research Assistant Professor in Engineering Education at Texas State University.
Reference
Amsel, E., Goodman, G., Savoi, D., & Clark, M. (1996). The development of reasoning about causal and noncausal influences on levers. Child Development, 67 (4), 1624-1646. doi:10.1111/j.1467-8624.1996.tb01818.x
Barlex, D., & Pitt, J. (2000). Interaction: The relationship between science and design and technology in the secondary curriculum . London, United Kingdom: Engineering Council.
Baxter, G., & Junker, B. W. (2001, April). Designing cognitive-developmental assessments: A case study in proportional reasoning . Paper presented at the Annual Meeting of the National Council of Measurement in Education, Seattle, WA. Retrieved from http://www.stat.cmu.edu/~brian/rpm/baxterjunkerncme.pdf
Ben-Chaim, D., Fey, J. T., Fitzgerald, W. M., Benedetto, C., & Miller, J. (1998). Proportional reasoning among 7th grade students with different curricular experiences. Educational Studies in Mathematics, 36 (3), 247-273. doi:10.1023/A:1003235712092
Behr, M., Harel, G., Post, T., & Lesh, R. (1987). Theoretical analysis: Structure and hierarchy, missing value proportion problems. In J. C. Bergeron, N. Herscovics, & C. Kieran (Eds.), Proceedings of the Eleventh International Conference: Psychology of Mathematics Education PME-XI (Vol. II, pp. 269-274). Montreal, Canada: International Group for the Psychology of Mathematics Education.
Borasi, R. (1986). On the nature of problems. Educational Studies in Mathematics, 17 (2), 125-141. doi:10.1007/BF00311517
Carpenter, T. P., & Moser, J. M. (1984). The acquisition of addition and subtraction concepts in grades one through three. Journal for Research in Mathematics Education, 15 (3), 179-203.
Carraher, T. N., Carraher, D., & Schliemann, A. D. (1985). Mathematics in the streets and in schools. British Journal of Developmental Psychology, 3 , 21-29. doi:10.1111/j.2044-835X.1985.tb00951.x
Chevallard, Y. (1990). On mathematics education and culture: Critical afterthoughts. Educational Studies in Mathematics, 21 (1), 3-27. doi:10.1007/BF00311013
Chevallard, Y. (2007). Readjusting didactics to a changing epistemology. European Educational Research Journal, 6 (2), 131-134. doi:10.2304/eerj.2007.6.2.131
Clements, D. H., & Sarama, J. (2007). Early childhood mathematics learning. In F. K. Lester, Jr. (Ed.), Second handbook of research on mathematics teaching and learning (Vol. 1, pp. 461-555). Charlotte, NC: Information Age.
Cross, N. (2007). Forty years of design research. Design Research Quarterly, 2 (1), 3-5. Retrieved from http://www.drsq.org/issues/drq2-1.pdf
Foster, P. N., & Wright, M. D. (2001). How children think and feel about design and technology: Two case studies. Journal of Industrial Teacher Education, 38 (2), 40-64. Retrieved from http://scholar.lib.vt.edu/ejournals/JITE/v38n2/foster.html
Deming, W. E. (1986). Out of the crisis . Cambridge, MA: MIT Press.
Harel, G., Behr, M., Post, T., & Lesh, R. (1987). Qualitative differences among 7th grade children in solving a non-numerical proportional reasoning blocks task. In J. C. Bergeron, N. Herscovics, & C. Kieran (Eds.), Proceedings of the Eleventh International Conference, Psychology of Mathematics Education PME-XI (Vol. II, pp. 282-288). Montreal, Canada: International Group for the Psychology of Mathematics Education.
Karplus, R., Pulos, S., & Stage, E. (1983). Proportional reasoning of early adolescents. In R. Lesh & M. Landau (Eds.), Acquisition of mathematical concepts and processes (pp. 45-90). New York, NY: Academic Press.
Katehi, L., Pearson, G., & Feder, M. (2009), The status and nature of K-12 engineering education in the United States. The Bridge, 39 (3), 5-10. Retrieved from https://www.nae.edu/Publications/Bridge/16145/16161.aspx
Kaput, J. J., & West, M. M. (1994). Missing-value proportional reasoning problems: Factors affecting informal reasoning patterns. In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (Research in Mathematics Education Series, pp. 235-287). Albany, NY: State University of New York Press.
Lamon, S. J. (1993). Ratio and proportion: Connecting content and children's thinking. Journal for Research in Mathematics Education, 24 (1), 41-61.
Langrall, C. W., & Swafford, J. (2000). Three balloons for two dollars: Developing proportional reasoning. Mathematics Teaching in the Middle School, 6 (4), 254-261.
Martínez Ortiz, A. (2004). Using the engineering design process to develop a framework & an approach for integrating engineering into the elementary classroom science curriculum . Unpublished manuscript, Tufts University, Medford, MA.
Martínez Ortiz, A. (2005). Fusing engineering-integrated engineering LEGO robotics and mathematics: An elementary classroom curriculum . Unpublished manuscript, Tufts University, Medford, MA.
Martínez Ortiz, A. (2008). The impact of engineering education at the kindergarten to high school levels: A review of research (Qualifying paper). Tufts University, Medford, MA. Retrieved from http://dl.tufts.edu/catalog/tufts:UA071.001.001.00006.00002
Martínez Ortiz, A. (2011). Fifth grade students' understanding of ratio and proportion in an engineering robotics program . Paper presented at the 2011 American Society for Engineering Education Conference, Vancouver, British Columbia, Canada. Retrieved from http://www.asee.org/public/conferences/1/papers/2649/view
Massachusetts Department of Education. (2001). Massachusetts science and technology/engineering curriculum framework . Retrieved from http://www.doe.mass.edu/frameworks/scitech/2001/0501.pdf
Misailidou, C., & Williams, J. (2003). Diagnostic assessment of children's proportional reasoning. The Journal of Mathematical Behavior, 22 (3), 335-368. doi:10.1016/S0732-3123(03)00025-7
Moundridou, M., & Kaniglonou, A. (2008). Using LEGO MINDSTORMS as an instructional aid in technical and vocational secondary education: Experiences from an empirical case study. In P. Dillenbourg & M. Specht (Eds.), Times of Convergence. Technologies Across Learning Contexts (pp. 312-321). Berlin, Germany: Springer-Verlag. doi:10.1007/978-3-540-87605-2_35
Museum of Science. (n.d.). The engineering design process. Retrieved from http://www.mos.org/eie/engineering_design.php
U.S. Department of Education, National Assessment Governing Board. (2014). Technology and engineering literacy framework for the 2014 national assessment of educational progress . Washington, DC: Author.
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics . Washington, DC: Author. Retrieved from http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf
Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas . New York, NY: Basic Books.
Puntambekar, S., & Kolodner, J. L. (2005). Toward implementing distributed scaffolding: Helping students learn science from design. Journal of Research in Science Teaching, 42 (2), 185-217. doi:10.1002/tea.20048
Resnick, M., Martin, F., Sargent, R., & Silverman, B. (1996). Programmable bricks: Toys to think with. IBM Systems Journal, 35 (3-4), 443-452. doi:10.1147/sj.353.0443
Roden, C. (1995). Young children's learning strategies in design and technology. In J. S. Smith (Ed.), IDATER 95: International Conference on Design and Technology Educational Research and Curriculum Development (pp. 21-27). Loughborough, UK: Loughborough University of Technology. Retrieved from https://dspace.lboro.ac.uk/2134/1521
Shewhart, W. A. (1986). Statistical method from the viewpoint of quality control. W. E. Deming (Ed.). New York, NY: Dover.
Texas Education Agency. (2008). Chapter 111. Texas essential knowledge and skills for mathematics . Austin, TX: Author. Retrieved from http://ritter.tea.state.tx.us/rules/tac/chapter111/index.html
Tourniaire, F. (1986). Proportions in elementary school. Educational Studies in Mathematics, 17 (4), 401-412. doi:10.1007/BF00311327
Vergnaud, G. (1983). Multiplicative structures. In R. Lesh & M. Landau (Eds.), Acquisition of mathematics concepts and processes (pp. 127-174). New York, NY: Academic Press.