JVER v28n3 - Developing Authentic, Integrated, Standards-Based Mathematics Curriculum: [More Than Just] An Interdisciplinary Collaborative Approach

Developing Authentic, Integrated, Standards-Based Mathematics Curriculum: [More Than Just] An Interdisciplinary Collaborative Approach

Victor M. Hernández
Center for Educational Technologies
Wheeling Jesuit University
Jonathan L. Brendefur
Boise State University

Abstract

We analyzed the collaborative process of mathematics and vocational-technical education (VTE) instructors in eight sites, located across the United States, as they developed one authentic, integrated mathematics curriculum unit. Over two years, we collected data on teachers' viewpoints on instruction, integration, and mathematics/VTE reforms. Site visits were conducted to gather additional information on teachers' views, teaching practices, collaboration process, school context, and quality of curriculum units. We found that although the quality of the units varied, the overall analysis suggested that is it is possible for interdisciplinary teams of teachers to create high quality integrated mathematics curriculum units if certain conditions are met. Having support from the school's community, meeting regularly with all the team members, focusing conversations toward student understanding, writing tasks that promote conceptual and integrated understanding of the concepts, and writing the unit together with reflective thought, all seemed to be critical elements in successful integrated unit writing .

Introduction

Over the last decade, interdisciplinary teacher collaboration has been identified as an important avenue for supporting the integration of academic and vocational education in authentic ways ( Bottoms & Sharpe, 1996 ; Grubb, 1995 ). This is particularly relevant to advancing the efforts for improving mathematics curriculum, teaching, and learning through contextual, authentic activities advocated in the National Council of Teachers of Mathematics standards documents ( NCTM, 1989 ; 2000 ) and in strengthening the type of mathematical activities conducted in vocational courses. The problem is we know little about specific dynamics and factors that facilitate the interdisciplinary work of mathematics and vocational education teachers.

The purpose of this study was to examine and describe an interdisciplinary, collaborative approach to produce and implement curricular units by focusing on three aspects of current reform efforts in mathematics and vocational-technical education: integration, authenticity, and use of standards. Specifically, the study had five objectives: (a) To describe teachers' shared understandings of mathematics and vocational-technical education reform principles and beliefs on authentic teaching practices; (b) to identify team collaboration patterns and strategies; (c) to describe the role of school supports in facilitating teacher collaboration; (d) to determine the level of authenticity (or intellectual quality) of curriculum units produced by interdisciplinary teacher-teams; and (e) to identify conditions promoting or hindering the quality of curriculum units.

The impetus behind this study was the increasing evidence suggesting that American students lack the skills needed for using mathematical knowledge in applied contexts ( Mathematical Sciences Education Board, 1995 ). One reason for this phenomenon is that American teachers' instructional practices often do not align with current school reform principles even though teachers may be familiar with them (e.g., Stigler & Hiebert, 1999 ). In general, it appears American teachers have difficulty implementing needed instructional changes and continue to focus on memorization of information, paper-and-pencil work, lecture methods, and extensive content coverage with little relevancy to student's contemporary needs ( National Center for Education Statistics [NCES], 1996 ; Porter, Kirst, Osthoff, Smithson, & Schneider, 1994 ; Spillane & Zeuli, 1999 ). As a result, researchers, policymakers, and practitioners have called for improved patterns of practice in the context of mathematics reforms. Research has also suggested that successful collaborative efforts should be built around a framework for authentic, standards-based curriculum, teaching, and learning, and should include appropriate teacher supports ( Betances, 1999 ; Newmann & Wehlage, 1995 ; Nickolas, 2000 ).

The conceptual framework for this study linked the principles derived from the National Council of Teachers of Mathematics [NCTM] standards documents ( 1989 , 1991 , 1995 ) and the reform movement in vocational-technical education [VTE] ( Dougherty & Ellibee, 1996 ). The study was further supported by research addressing the development of organizational capacity in the schools to examine critical supports and processes leading to successful, collaborative curriculum development practices of mathematics and VTE teachers.

Framework for Standards-Based Curriculum

NCTM has played an active role in promoting reforms in mathematics education. Its vision for curriculum and evaluation provides a comprehensive framework suggesting improvements for K-12 mathematics ( NCTM, 1989 ; 2000 ). The NCTM vision advocates that all students should participate in powerful mathematics learning, develop confidence through relevant problem solving activities, and establish practical, conceptual connections within mathematics and across other disciplines. To guide teachers in this work, teaching and assessment standards were subsequently published by NCTM (1991 ; 1995 ). Concurrently, similar reforms have been promoted in the VTE sector. Derived from changing technologies and modus operandi of global markets, new skills involving problem solving, teamwork, reasoning, and communication have been demanded of the workforce and future workers who are prepared in secondary and postsecondary education programs ( Gray & Herr, 1995 ; Wirth, 1992 ). To face this challenge, reform advocates proposed to move from a traditional, segregated, job-specific VTE system to one that would bridge vocational and academic education, school and work, and secondary-postsecondary levels ( Grubb, 1997 ; Phelps, 1992 ; Phelps, Hernández-Gantes, Jones, Sanchez, & Nieri, 1995 ; Mathematical Sciences Education Board, 1995 ).

The reform movements in mathematics and VTE share common grounds: (a) a belief that all students can benefit from challenging education regardless of learning abilities or career interests, and (b) an understanding that learning has to be more relevant to students within the context of today's world. Under these premises, the prospects for linking mathematics and career concepts with an added emphasis on problem solving, critical thinking, and communication skills appeared promising. The combined principles of these two reform movements provide further impetus for systemic reform in curriculum and instruction. The challenges are to develop shared understandings of integrated, authentic, standards-based mathematics curricula and to discover how to encourage collaborative curriculum development of this nature.

Standards-based curricula were defined in this study by teaching and learning that aligned with the parameters proposed by the NCTM Standards for School Mathematics (1989) . For two-year colleges, a similar framework has been provided by the Standards for Introductory College Mathematics Before Calculus ( American Mathematical Association of Two-Year Colleges, 1995 ). Concurrently, the National Center for Research in Vocational Education (NCRVE) developed a set of standards for evaluation of high quality school-to-work curricula ( Dougherty & Ellibee, 1996 ). All of these frameworks share common criteria for good teaching practices, emphasizing problem solving, communication, reasoning, and connections for curriculum integration.

Research on Authentic Curriculum and Instruction

The notion of authentic curriculum and instruction is an underlying descriptor of intellectual quality. In other words, authentic curricula engage students in work that is grounded in activities with the purpose of building disciplinary knowledge through real and substantive material. The intellectual quality is created when students are encouraged to study material in deep and connected ways that have value beyond doing the work for schools' sake ( Brown, Collins, & Duguid, 1989 ; Newmann & Wehlage, 1995 ). Under this premise, teaching and learning requires students to confront problems relevant to them and their surroundings. The goal is to promote increased academic achievement by problem solving, reasoning, and communicating about real-world social and work situations. Both the NCTM Standards and the reform movement in VTE emphasize the contextual nature of authentic student activities. In innovative VTE programs these authentic connections may be emphasized through actual work activities as a means to provide students with opportunities to connect academic and occupational concepts and skills ( Grubb, 1995 ; Phelps, et al., 1995 ).

Based on the work of Newmann & Associates (1996) , authentic achievement was defined in the study by four components that promote improved student performance: higher-order thinking (HOT), deep knowledge, substantive conversation, and connections beyond the classroom (see also Newmann, Secada, & Wehlage, 1996 ; Newmann & Wehlage, 1995 ). Higher order thinking is manifested when students manipulate information and ideas by synthesizing, generalizing, explaining, hypothesizing or arriving at conclusions, which produce new meanings and understandings for them. Deep knowledge requires students to address in-depth major mathematical and vocational ideas with the purpose of creating complex student understandings. Substantive conversation is characterized by students engaging in extended exchanges with teachers and/or peers in a way that builds an improved and shared understanding of mathematics and career concepts. The final component of authentic curriculum, connections to the world beyond the classroom , requires students to make meaningful links between substantive mathematics knowledge and occupational applications.

Research on Mathematics and Vocational-Technical Education Integration

A clear understanding of curriculum integration is also essential for guiding collaborative work of mathematics and VTE instructors. Integrated curricula emphasize understanding of mathematical concepts rooted in occupational contexts. That is, mathematical content can be aligned with broadly defined occupational areas so students become immersed in integrated applications that are relevant to them. In integrated learning, the foundations of mathematics are fused with occupational, career, and life-skill content through models ranging from individual teachers integrating content in lessons to teacher-teams integrating curriculum in career academies ( Bottoms & Sharpe, 1996 ; Dougherty & Ellibee, 1996 ; Grubb, 1997 ).

The School-to-Work Opportunities Act of 1994 (STWOA) ( U.S. Congress, 1994 ) further encouraged the integration of academic and career competencies that are contemporary and transferable across broadly defined technical fields. STWOA also provided broad guidelines for implementation of suggested reforms that would link both academic and practical skills. However, a national survey of programs featuring mathematics and VTE integration collaborations described these integrated reform efforts as negligible and slowly evolving. In general, simplistic forms of collaboration (e.g., individual teachers integrating content informally) with a weak emphasis on the NCTM standards were found in this study ( Hernández-Gantes & Nieri, 1997 ). Among other factors, a lack of shared understanding of principles behind current reform movements appears to limit the natural evolution of these collaborative efforts ( Betances, 1999 ; Grubb, 1997 ; Locke, 1999 ; Porter, et al., 1994 ; Spillane & Zeuli, 1999 ). To fill the integrated (or applied) curriculum void, a number of commercial curriculum products have mushroomed under the label of applied mathematics claiming alignment with the relevant standards. Although helpful in complementing instruction, the generic nature of these products limits their application to individual curricular needs found in a variety of potential integrated contexts (e.g., contextual mathematics in agriculture, electronics, architecture, and manufacturing). Another problem with these applied curriculum materials or courses is the tendency to involve very basic skills rather than higher order thinking skills ( Bottoms & Sharpe, 1996 ; Stasz, Kaganoff, & Eden, 1994 ).

While in theory the integration of mathematics and VTE appears promising, there are a number of institutional obstacles that limit its implementation. Two problems seem to be most prominent: restricted instructor collaboration fostered by traditionally segregated academic and VTE tracks, and applied curricula, which still rely on traditional methods of teaching, learning, and assessment. And yet, there are hints of evidence that in schools where teacher collaboration is encouraged, it is possible to observe highly authentic learning activities that reflect the NCTM standards ( Kruse, Seashore, & Bryk, 1994 ; Newmann, et al., 1996 ; Nickolas, 2000 ).

Research on Collaborative Curriculum Development

Recent studies have demonstrated that ideas for reform and schools' commitment for implementation do not guarantee success in improving student learning ( Locke, 1999 ; Peterson, McCarthey, & Elmore, 1996 ; Porter et al., 1994) . More than just commitment for a collaborative approach may be required to develop and implement curricula that meet reform principles. Given these circumstances, it is not surprising that efforts to develop integrated, authentic, standards-based mathematics curricula are generally negligible.

Research on organizational restructuring offers some possible explanations and suggestions for building collaboration to implement reform in terms of curriculum restructuring and classroom instruction ( Adajian, 1995 ; Kruse et al., 1994 ; Newmann & Wehlage, 1995 ; Peterson et al., 1996 ). Peterson et al (1996) argued that teachers who are committed to change are strongly motivated to improve their practices and will strive regardless of changes in organizational structures. Once teachers begin to share a common understanding of good practice, Peterson et al noted, they also would need new school structures to maintain their efforts. Ultimately, they suggested teachers' commitment to change might be a function of their "beliefs, understandings, and behaviors in the context of specific problems in the classroom" (p. 147). Further, when interdisciplinary work is involved, these factors may present serious barriers for promotion of collaborative work ( Schmidt, Finch, Faulkner, & Kandies, 1995 ).

To foster effective collaboration it may be necessary to involve both mathematics and vocational-technical instructors in the conversation on restructuring and to share leadership responsibilities with representatives from each group ( Hernández-Gantes & Nieri, 1997 ). Research on organizational restructuring suggests that systemic reform is an institution wide enterprise requiring a professional community of instructors ( Adajian, 1995 ). In schools where instructors share this sense of professional community, they are more likely to collaborate. But collaboration alone is not a guarantee that integrated curriculum development and teaching will improve or increase academic achievement. To nurture successful integrated activities and support for sustained quality of collaborative work, schools should provide instructors with time to reflect on common challenges, observe each other's teaching, agree on student expectations, and develop shared understandings of principles which underlie school reform ( Kruse et al., 1994 ; Newmann & Wehlage, 1995 ).

To summarize, while it is important for instructors to have converging frameworks for developing integrated, authentic, standards-based mathematics curricula, it is equally critical to understand the conditions that enable and hinder them in this process. By examining teacher-teams committed to interdisciplinary collaborative work in designing such curricular units, it may be possible to build an understanding of the supporting factors for developing authentic, standards-based curriculum.

Method

Data for this research derived from the evaluation component of a collaborative curriculum development effort supported by a national integration demonstration project. Throughout this document, this project is referred to as MathNet.

Participants

Project staff collaborated with 20 instructors and curriculum specialists who represented seven high schools located in California, Kentucky, Michigan, Minnesota, New Jersey, South Carolina, and Wisconsin, and a two-year community college located in Texas. Teams were composed of two-three members including at least one mathematics and one VTE instructor, as well as a curriculum specialists in some instances. The role of the curriculum specialists was to advise the local team on curriculum writing. Due to the nature of its proposed curriculum unit, one of the teams also included a science teacher.

Selection of teams was done through an initial national nomination process that resulted in a pool of 82 schools. The initial screening involved a review of the extent of integration of vocational education and mathematics with particular emphasis on implementing the NCTM standards. Based on this screening, a third of the schools were invited to submit an application for participation. Upon review of applications, eight teacher-teams were selected based on the extent of integration efforts, experience in curriculum development, working vision for implementing the NCTM standards, and the quality of the team's proposed plans for developing integrated curriculum. The review process involved ratings from five project staff and input from the project's advisory group. The highest-rated teams from urban, suburban, and rural sites were chosen for participation in the project. A brief description of the schools is provided in the Appendix. The charge for selected teams was to produce, field test, and revise one authentic, integrated curriculum unit for use in grades 9-12 and two-year, college-level mathematics as appropriate.

MathNET Support

All selected teams participated in a weeklong summer institute in Years 1 and 2. In the initial summer institute teachers were provided with technical assistance leading to the development of understandings about integration, implementing standards, and curriculum writing. Initial ideas for curriculum units resulted from participation in the first summer institute. With consulting support from project staff, teams spent the following school year developing a curriculum unit. Support staff was comprised of an experienced mathematics teacher on both the implementation of NCTM standards and integration practices. A second member provided assistance on assessment issues. A third member contributed with expertise on VTE curriculum and collaborative practices.

Further assistance in refining final versions of curriculum units and on strategies to evaluate products was provided to teams during and after the second summer institute. Throughout the two-year project, two staff members visited each team for 1-2 days to provide on-site technical assistance, observe units being taught, discuss observations with team members, and answer questions related to writing the units as needed. In addition, staff members were available to consult with teams on issues related to the development of their curriculum units. After each summer institute, support staff tracked progress on curriculum units, conducted reviews of team products, and provided ongoing feedback.

Research Questions and Data Sources/Instrumentation

Drawing on previous research and related literature, five major questions guided the study:

1. What are the participants' shared understandings of mathematics/VTE reform principles and beliefs on authentic teaching practices?
2. What are the patterns and strategies for team collaboration?
3. What school supports and structures facilitate teacher collaboration?
4. What is the level of authenticity of integrated curriculum units?
5. What conditions promote high quality of curriculum units?

To answer these questions, various sources of data were collected and analyzed through qualitative research techniques ( Merriam, 1998 ; Spradley, 1979 ; Stake, 1994 ; Strauss, 1987 ; Wolcott, 1994 ). Table 1 summarizes the areas of interest for data collection, data sources, instrumentation, and frequency of data collection.

Table 1
Data Collection Strategies: Areas of Interest, Sources, Instrumentation, and Frequency.

Area of Interest	Data Sources and Instrumentation	Frequency of Data Collection
Baseline Information	Application materials . Provided preliminary information on school context, team characteristics, integration efforts, and experience in collaborative work. Preliminary Instructor Survey . Provided baseline data on teachers' background including beliefs on instruction and professional development needs.	Collected once and used for team selection purposes. Collected at the outset of the project.
Collaborative Curriculum Development Process	Individual and Team Interviews . The interview protocols addressed teachers' ideas about pedagogical issues, collaboration, and perspectives on quality curriculum development. Classroom Observations . The protocol for classroom observations yielded behavioral data on instructional practices in relation to criteria for authentic pedagogy. Consulting Documentation . Trail of correspondence between teams and project staff in electronic and paper form provided insights on general curriculum development issues.	Collected at two summer institutes and 1-3 site visits depending on location. Collected during site visits (1-3 site visits depending on location). Collected during year following participation in summer institutes.
Curriculum Units	Curriculum Review Form . The review form provided data on the quality of curriculum units in relation to criteria for authenticity. Documentation of Feedback and Follow- Up . Trail of correspondence between teams and project staff in electronic and paper form provided insights on specific curriculum development issues and strategies for improving curriculum units.	Collected from at least two drafts of curriculum units. Collected during year following participation in summer institutes.

Data Collection and Procedures

Initially, the participants were requested to complete an extensive preliminary instructor survey. The survey was complemented with an individual semi-structured interview to collect data on teachers' typical classroom practices. The teams then participated in a week-long summer institute which allowed them to begin developing their units and to learn more about the three major features of expected curriculum development efforts: integration, authenticity, and use of standards. Team, semi-structured interviews were also used during the middle of the project and again at the end to determine supports and barriers that led to the creation and implementation of highly authentic units ( Newmann & Associates, 1996 ). Data was also collected through classroom observations and evaluation of curriculum units. Additional data was collected through discussions of follow-up technical assistance provided by MathNet staff to all teams. The trail of interactions between project staff and teams provided insights on team understandings, collaboration factors, and curriculum development strategies.

Analysis

For the analysis aligned with research questions 1 and 2, data from the preliminary instructor survey was summarized using descriptive statistics and used as baseline reference. Complementary data from individual and team interviews was analyzed using a systematic comparative method ( Glaser & Strauss, 1967 ; Merriam, 1998 ). Under this method, we first compared critical perspectives and ideas deemed important by participants under broad themes. Next, we characterized each theme using categories of perspectives/ideas. The categories were further verified for consistency within and across teams.

To address question 3, the analysis of school supports was guided by Lisa Adajian's (1995) model of professional community. Through a systematic approach of examining the interview data, each team was rated on the four criteria listed below.

1. De-privatization: Access to other teachers' classroom by visiting, observing, or assisting in some way.
2. Shared sense of purpose: Colleagues shared similar pedagogical beliefs.
3. School-wide collaboration: Staff met regularly to discuss ideas such as integration, standards, or authenticity.
4. Structural supports: Administration encouraged and assisted them in combining classes and adjusting school schedules to meet the needs of the integrated units.

Each team received two points if they met the criteria, one point if it was mixed, and zero points if no evidence was found. Evidence was documented through interview data and notes collected during site visits.

To address question 4, project staff reviewed initial drafts of curriculum units using criteria derived from the NCTM standards framework and authentic instruction ( Newmann et al., 1996 ) to determine the extent and nature of integration and authenticity. This information was used as a baseline of the degree to which the units were meeting the criteria for integration, standards, and intellectual quality or authenticity, and to assist teams of teachers in rewriting their units. The criteria for authenticity included depth of understanding, conceptual grounding of content, elaborated communication, and experience beyond success in school. These constructs were adapted from scales developed by the Center on Organization and Restructuring of Schools (CORS) (see Secada & Byrd, 1993 ; Brendefur, 1996 ).

The first domain, depth of understanding , examined whether the unit required or encouraged students to organize, interpret, evaluate, synthesize, or, in some other way, work with complex information to understand a particular concept, claim, problem, or issue. Depth of understanding requires focused attention on a particular problem, issue, or question. It is promoted when the lesson calls for awareness of alternative solutions, perspectives, or points of view, even though a single answer or solution may be considered unequivocally the best by diverse authorities. The second domain, conceptual grounding of content, examined whether the unit required students to work with significant and substantive material and with approaches to inquiry important to mathematics and vocational-technical courses. Each lesson must consider the appropriateness and accuracy of the content and processes encountered by students in the two disciplines. The third domain, elaborated communication , examined whether lessons required students to elaborate on their ideas and conclusions through extended writing or oral presentations. A lesson was regarded as being more authentic when students had ample opportunities to explain generalizations, classifications and relationships relevant to a situation, problem, theme, or to justify their thinking. Examples included attempts to argue, convince, or persuade and to develop or test hypotheses. When the lesson required little more than giving results or asking students to show little work or to write brief sentences, it was regarded as less authentic.

Finally, experience beyond success in school , examined the extent to which lessons had meaning to students so that they could make concept connections with real-world situations. This construct shares two essential features: (a) whether the problem, question or issue posed by the lesson is or is likely to connect students with situations beyond the classroom setting, and (b) whether students can communicate results to an audience other than the teacher and peers (e.g., worksite mentors). Important findings on effective collaborative practices and processes emerged from our constant comparative analysis of data within and across participating instructor teams.

Guided by these constructs, complementary analyses of interviews, classroom observations, and documentation of technical assistance were conducted following the constant comparative techniques to address question 5 ( Merriam, 1998 ). This overall analysis yielded insights on conditions that facilitated or hindered the quality of curriculum units produced by teacher-teams.

Findings

We introduce the findings with the teachers' notions of integration and authenticity. Next, we present team collaborative patterns and highlight the school context in which teams worked. This is followed by results on the quality of curriculum units produced by teacher-teams. We close with a presentation of findings on factors and conditions that promote high quality integrated curriculum units.

Teachers' Notions of Integration and Authenticity

The understanding of the twenty participating teachers about integration and authenticity was captured through an initial questionnaire and individual interviews. Each member was rated on whether their beliefs were consistent, mixed, or inconsistent with project definitions of the two constructs.

Notions on integration . The teachers' understandings of integration of mathematics and VTE were classified into five categories: applied mathematics, theoretical foundations for integration, mathematics modeling derived from integration, mathematics in real-world situations, and impact on improving students' understanding of integrated content.

In the first category, the teachers' notions of applied mathematics focused on using mathematical rules and algorithms in occupational contexts or related to VTE courses carrying titles such as Applied Math, Basic Math, or Occupational Math. In general, mathematics is trivialized in these applied courses. Even though applications to real-world problem situations may be emphasized, they are usually disjointed and removed from students' interests since connections to a series of sequenced and coherent career concepts are not possible. Furthermore, students are encouraged to memorize one specific way to solve problems. Five of the twenty teachers' responses fit into this category. These five teachers were dispersed among the different teams, indicating that each team had to overcome differences in basic understandings about applied versus authentic mathematics. The second category, application of theoretical foundations for integration , examined how an occupational context can be used as an example to help explain a mathematical theory. Some teachers clearly articulated that integration is using vocational contexts to develop and reinforce a mathematical concept or theme. Both of these first two categories show a misapplication or trivialization of one course of study over the other.

The third category examined integration in terms of mathematics modeling . In this category math is used as a method to explain or model what is happening in a real-world context. Only two teachers characterized integration in this particular powerful way. However, this is still not seen as true integration in that the mathematics (or mathematics course) is being driven by the vocational-technical activities or situations.

The fourth category, real-world use of mathematics , was initially articulated by seven of the twenty teachers, more than in any other category. Integration was perceived as a way to include real-world situations in a mathematics class to either motivate students or to see where mathematics might be used in the real-world context. Here the mathematics course is using the vocational-technical concepts to assist furthering the mathematical concepts.

Finally, the fifth category focused on improving students' understanding of both mathematics and career concepts. Three of the teachers stated that the integration of mathematics and VTE would increase students' understanding of the content in both areas as well as how concepts are interconnected across disciplines. This type of integration is the most difficult to achieve because it asks instructors from both courses of study to modify their curriculum in a way that supports each other's ideas as well as support student understanding. It might be the case that this integrated unit could be taught equally well in both a mathematics course and vocational-technical course without a loss of content to one subject over the other.

Notions of authenticity . Authenticity was described earlier in this study as student work that requires deep understanding of mathematical and career concepts and contexts by producing or constructing knowledge through in-depth exploration and substantive conversations of topics that have some value beyond the classroom. The analysis indicated that most teachers only understood authenticity as math being relevant to real-world or occupational settings. For example, teachers described authenticity as "showing connections relevant to use in a work situation" or "going beyond the classroom and really hitting on what's out there in the world." Many of these teachers added that real-world situations were useful to motivate students and to help them see where mathematics might be applied.

Only five of the teachers were able to connect the concept of authenticity to other important factors that went beyond relevancy to realistic situations. For these teachers who were aware of the broader implications for designing authentic curricula, authenticity implied opportunities to problem-solve and think critically about problems.

Interdisciplinary Collaborative Patterns and Strategies

A shared understanding of effective curriculum development served as the backdrop for examining collaboration patterns and strategies used by teacher-teams to produce curriculum units.

Collaboration Patterns . Five of the eight teams had previously worked together on integrating mathematics and vocational contexts, while the other three had formed an ad hoc team for the project. The teams who had worked together in the past, and who were building upon course material previously taught, designed units that showed a more coherent understanding of integration ideas. In contrast, teams who had not worked together before tended to rely on the individual expertise of "dominant" members who appeared more knowledgeable and whose ideas seemed to be expressed with more passion and vigor. As collaboration continued and changes were made that challenged perspectives of mathematics and VTE teachers, teams began to realize that each member had something valuable to contribute. During the first year, evolution toward more democratic input between team members took shape within six of the eight groups.

The collaborative process also varied between teams from highly collaborative to individual efforts. For instance, the collaborative process of one of the more highly collaborative teams could be best described as an iterative process of reflection, writing, and pilot testing. The members of the team would usually ask the question, "What do we really want them to learn?" as the critical element pervading each meeting. They mused over this question during the entire project.

In the individually-led efforts, which included four of the eight teams, the process for refining curriculum ideas was more cumbersome. Here, individual teachers took it upon themselves to provide the leadership in developing curriculum ideas for the team and bringing everybody else into the fold. The dominant member would seek specific input from other team members and the responsibility for developing ideas concentrated on the team leader.

Team strategies . An important factor influencing the development of curriculum units was the strategies each team used in creating the unit. Each team's approach to writing a unit was classified by whether main ideas originated during the project or from an activity done before by a member. Half of the teams' initial ideas for integrated curriculum units stemmed from prior integration work or ideas. For example, one team's unit derived from the technology teacher's bridge-building activity, which he had used previously in his class. At this point, the math and physics teachers discussed from their respective disciplines critical ideas in bridge building. Substantive conversations ensued, resulting in richer activities for the students. These activities incorporated mathematical models to test important ideas in physics related to bridges such as tension, compression, and torque.

Another strategy to facilitate collaborative work was the approach each team followed to address the focus of the unit. Three teams emphasized instructional activities that focused on student understanding of mathematics and its applications: the fifth category of integration discussed earlier. After pilot-testing their units, these teams restructured lessons, refined their questions, and created more mathematical situations throughout the entire unit to focus on the development of student understanding. As one teacher put it: "We really focused on asking one question and then tried to have the students investigate that particular question and come up with an answer for one idea, one question-not to make it too broad, too general."

The other five teams were more interested in featuring "interesting" student activities to get students engaged in "hands-on" learning. This approach was related to their beliefs that integration of mathematics and vocational-technical ideas should motivate students to learn something "interesting." In these cases, curriculum units tended to focus on applied learning activities reflecting more traditional pedagogical practices (e.g., step-by-step procedures).

The Role of School Supports

Based on research suggesting that a school's context (or professional community), affects classroom practices ( Adajian, 1995 ), we examined each school on four areas: de-privatization, shared sense of purpose, extent of staff collaboration within the school, and structural supports. Data about each school's context were collected through semi-structured team and individual interviews, and each area was rated on a three-point scale (see Figure 1).

Figure 1 . Degree of Professional Community Observed for Each Team.

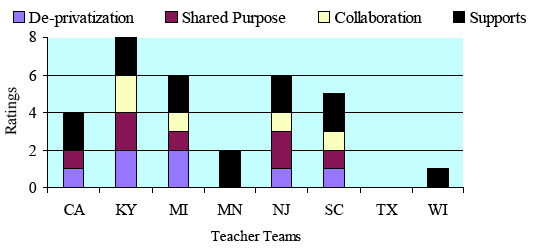
De-privatization practices were defined as access to other teachers' classrooms by visiting, observing, or assisting in some way. Five teams (CA, KY, MI, NJ, and SC) enjoyed various levels of de-privatization ranging from somewhat to highly supportive practices. The New Jersey team depicted their administration as supportive, allowing de-privatization and collaboration among staff about issues they felt important, but the administration did nothing else to encourage teachers to integrate. Only one district administrator had visited their classrooms to watch the unit being taught, not the principal, not the department chair. Other staff members were indifferent towards integration.

Finding a shared sense of purpose (colleagues sharing similar pedagogical beliefs) within each of the participant schools was more problematic. Interview data showed a strong commitment toward improving the quality of students' learning at only two sites (KY and NJ) and a weak shared commitment at three other sites (CA, MI, and SC). In these latter cases, this shared purpose did not meet total agreement on integration issues, but the school culture encouraged the development of rigorous curriculum for students. In the rest of the sites, the shared purpose was either very traditional or non-existent.

School-wide collaboration (the extent to which staff met regularly to discuss ideas such as integration, standards, or authenticity) at participant sites was characterized as very limited. In only one site-Kentucky-was there strong evidence of school-wide collaboration. In this school, teachers worked together and constantly shared ideas. Other structural supports, such as the school's flexible schedule, also supported de-privatization, allowing teachers to team-teach one or two classes, have students move from one teacher to another, and have common preparation periods. At three other sites (MI, NJ, and SC) the picture of collaboration was mixed. At those sites, only a handful of innovative, yet isolated, teachers showed work on integration practices while the majority of their peers saw this work as cumbersome or not worth trying.

In six sites (CA, KY, MI, MN, NJ, and SC), structural supports were highly visible enabling teachers to work on integrated activities. At the Kentucky school site the community and administration supported integration activities. Each technical (e.g., welding, plastics, drafting, desktop publishing) teacher was assigned to be on a team with a mathematics, science, and communication teacher. The school's mission statement stated that through integrated course work students would learn to be effective workers in society. The administration allowed these different instructors to team-teach, move the same group of students from one teacher to the next, or use any plausible teaching scenario to get students to use technology. The rest of the teams experienced similar support with the exception of two teams whose school support was limited or nonexistent.

Quality of Curriculum Units

Overall, all teams slowly began writing units, negotiating perspectives on integration, content coverage, and teaching ideas. Much discussion took place but the collaborative process lacked a method for clarifying ideas in writing. Leadership within each team floundered due to lack of time and differing views on major ideas underlying proposed units. Initial drafts reflected a disjointed process, which was characterized by sketchy information loosely connecting integration, authenticity, and standards-based instructional activities. To address this issue, MathNet staff encouraged teachers to clarify ideas and express changes in writing, and teams finally realized the necessity of documenting their ideas and subsequent changes. At this point, teams began to express their curriculum ideas in detailed writing. It was only then that teams could go back to review weak ideas and make sense of changes. This new approach to developing curriculum was quite a contrast from the teams' beginning attempts in which revisions were difficult because little written documentation of ideas existed.

Throughout their curriculum development process, some teams produced three versions of their integrated units, each representing a different stage of development and quality. Due to unexpected conflicts in schedules some teams were only able to produce two versions. As expected, later versions rated higher on authenticity scales. The mean rating for initial versions of units was 14 (maximum rating possible = 45). The average rating improved five points (to 19) for the second version, and increased another two points (to 21) for the final version of the units (see Brendefur, Hernandez-Gantez, & Webb, 1998 , for details).

What does this mean? To begin, the initial units across teams, on average, contained few, if any, questions or tasks requiring students to make sense of information, think deeply about central ideas of the disciplines and topics, discuss or elaborate on ideas or products, or make connections to real-world situations. By the final version, two teams had units with a substantial amount of questions that required students to make sense of an important topic, examine the material with some thoroughness, discuss important ideas with each other, and see the relevance of their work to the real world. Another four units moved in this direction.

Although the quality of units improved as teams made revisions and learned from multiple implementations of the unit, the overall result signaled the difficulty in facilitating interdisciplinary curriculum development work.

Conditions that Impact Quality of Curriculum Units

Three important conditions appeared to have an impact on the quality of integrated curriculum units produced by teacher-teams. The conditions were associated with teachers' teaching practices, school supports, and collaborative patterns.

Authenticity of teaching practices . In general, teams with teachers whose practices were rated higher on the scales of authenticity tended to create team conditions to develop units that rated high on similar scales. This may be because these teachers already know how to ask and write questions that engage students in authentic types of activities. It also appeared that teachers whose pedagogical skills were rated higher tended to influence the type of activities/tasks found in the units (see Brendefur et al, 1998 for details). In short, a unit's score reflected the ideas of the teachers who scored highest on these scales. This may be because the member whose practices were more consistent with the project goals (integrated, authentic, and standards-based) tended to take more of the responsibility of writing and implementing the unit.

School context's impact on unit rating . Overall, half of the sites that showed moderate to high levels of support also showed higher ratings on the authenticity scales. The other half showed little school support and tended to rate low on the scales. It was clear from observations and interviews at the schools that the level of school support encouraged or hindered team members in going further in meeting authentic criteria. For example, school context might be one explanation for the Kentucky team's large gain on the scales of authenticity as compared to any of the other participating schools. The school was actively pursuing integration activities, and featured a career academy where integration of academic and VTE was encouraged. The team was used to giving and receiving feedback on curriculum development and instructional practices, and was receptive to suggestions for improving their integrated unit. In contrast, in schools with little collegial support, little teacher collaboration and no attempts to team-teach, and lack of a clear focus for integration efforts, the level of authenticity tended to rate low.

Impact of teacher collaboration on unit ratings . Overall, teams with high collaboration produced units that rated higher on the scales of authenticity. The New Jersey team typified this trend. Team members spent many hours each week individually and collectively discussing: (a) the content and concepts in the unit, (b) how students would and did react to tasks and questions, and (c) how to modify tasks and questions in the unit. This focus on conceptual knowledge and reflection of what works was an important factor in the success and high rating of the unit. Further, teams who had been working together for some time and were building upon prior integration ideas were more focused in writing integrated units. Even in cases where the team had to refocus the original idea, because they were building upon these prior experiences and collaboration, they were able to make continuous progress. In comparison, teams with problematic dynamics, lack of focused collaboration, and little prior teamwork usually showed lower ratings of curriculum units.

Conclusions and Discussion

The analysis of teachers' conceptions about integration and authenticity, the collaborative curriculum development process, school context, and quality of units were consistent with research on developing school organizational capacity ( Kruse et al., 1994 ; Newmann & Wehlage, 1995 ), academic and VTE integration ( Bottoms & Sharpe, 1996 ), and implementation of mathematics reform ( Porter et al., 1994 ; Spillane & Zeuli, 1999 ). Several conclusions emerged from the analysis of our findings.

The first conclusion derived from the study of teachers' understandings of integration and authenticity: When integrating mathematics and VTE, conflicting notions of what constitutes high quality integrated, authentic curriculum and instruction are magnified. Thus, the need to develop a base of shared "big-picture" understandings becomes an absolute necessity . For example, mathematics teachers brought to their teams strong ideas of content coverage, which favored procedural behaviors and guided instruction. VTE instructors contributed with show-and-tell ideas, but the teachers' collective beliefs missed making the natural connections to move curriculum and instruction to a higher level of authenticity. Although instructors believed in the benefits of mathematics and vocational-technical integration, their notions were those of "applied" curriculum. As a result, their units still lacked challenging student activities, which would elicit high levels of problem solving, reasoning, and communication from students. To create the foundations for successful and productive collaboration, instructors need to develop a base of shared understandings about important collaborative work concepts and opportunities for substantive interactions in the school ( Betances, 1999 ; Bottoms & Sharpe, 1996 ; Locke, 1999 ; Newmann & Wehlage, 1995 ; Nickolas, 2000 ).

Research on authentic instructional practices have documented that traditional beliefs on teaching practices are pervasive and translate into classroom activities which feature rote memorization and passive learning ( Newmann & Associates, 1996 ; Romberg & Carpenter, 1986 ). Newmann and Associates suggested that teachers should agree upon high expectations for student achievement and criteria for high-quality instruction (i.e., authenticity). It is indispensable to reach this consensus to build a base for designing highly authentic integrated mathematical tasks, yet bridging mathematics and VTE education perspectives add extra difficulties for reaching this agreement.

A second conclusion emerged from the analysis of the interdisciplinary collaborative process: When integrating mathematics and VTE guided by standards, it is critical to foster effective team dynamics and democratic discourse for successful collaborative curriculum development. Otherwise, teachers with strong beliefs and personalities will dominate the conversation imposing their ideas on others. Seniority may play a role in team dynamics and prevent open discourse and democratic input, especially if members have had no previous interdisciplinary collaboration experience. Furthermore, considering traditional, stereotypical perceptions of the inherent worth of mathematics compared to that of vocationaltechnical education, team dynamics might reflect an unwritten hierarchical status of players. The result of this hierarchical status on curriculum development might be reflected in low-levels of authenticity or curriculum, which is heavily biased toward one particular discipline. The theory on developing organizational capacity suggests a number of criteria to create an environment where teachers collaborate as a community of professionals. Time for shared planning, discussing ideas, and appreciating the contributions of each other in a holistic fashion are key elements for successful teacher collaboration ( Adajian, 1995 , Kruse et al., 1994 ; Newmann & Wehlage, 1995 ; Schmidt et al., 1995 ).

A third conclusion underscores the importance of the school context in facilitating interdisciplinary teacher collaboration: Effective interdisciplinary collaborative curriculum development is most likely to happen in schools that provide opportunities to collaborate across disciplines, foster a shared sense of purpose, and provide programmatic supports and flexible structures needed for genuine collaboration . Our findings were consistent with the literature on organizational capacity and teacher collaboration ( Peterson, et al., 1996 ; Betances, 1999 ; Locke, 1999 ; Schmidt et al., 1995 ). It was evident from observations and interviews that interdisciplinary teacher collaboration is a time-consuming activity with important implications for school culture and administrative supports. The focus of teacher collaboration may be easily lost or hindered in school environments where administrators and peers are not entirely convinced of the value of interdisciplinary activities. By comparison, it was clear that teams with supportive school environments and structural supports to collaborate, were able to stay focused and progressively refine the design of the teaching and learning activities included in their proposed units. It is imperative for schools to understand that it is not enough to encourage teachers to collaborate. Schools must be willing to provide needed structures, resources, and supports to facilitate productive collaboration.

Regarding the quality of curriculum units, a fourth conclusion reflects the holistic nature and conditional possibility of successful curriculum development: Highly authentic, integrated, and standards-based curriculum units could be produced if interdisciplinary teams collaborate under a set of favorable conditions. What are these conditions? Interdisciplinary teacher-teams should share similar conceptions of authenticity and integration, have prior experience collaborating in teams, work in a school committed to collaboration, and focus on teaching for increased understanding of concept connections and applications in occupational contexts. Based on our observations, interviews, and ratings of curriculum units, it was evident that successful collaborative curriculum development entailed more than just a collaborative approach. To be successful, it appears that all conditions should be in place. Even teams with strong backgrounds on one or two conditions but weak in others had difficulty developing high quality curriculum units. The implications for school-wide collaboration, for developing communities of learners in schools, and for professional development for both administrators and teachers are key elements in producing quality integrated units ( Peterson et al., 1996 ; Loucks-Horseley, Stiles, & Hewson, 1996 ).

Finally, our last conclusion is tied to the implications for professional development: Genuine collaborative curriculum development occurs when teams engage in reflective dialogue grounded in their own experiences, needs, and resources. The success of team collaborations can be enhanced by facilitating reflective dialogue rather than by directing the process with rigid models for technical assistance . Our analyses showed that teams could have developed curriculum units much faster if MathNet staff had provided more directed guidance from the beginning of the project as had been expected by teams. However, a "fill-inthe- blanks" model would have prevented important reflective dialogue about high quality, integrated, authentic instructional activities more relevant to the teams. Team dynamics would have been restricted to contrived individual contributions motivated by completing assigned sections in the way designated by project staff. In contrast, by encouraging teams to experiment and explore their own design approaches, a vehicle for self-examination was constructed, team dynamics began to evolve, and intrinsic motivation for genuine collaboration was generated. In this regard, a number of recommendations for professional development, which feature flexible collaboration and reflective dialogue have been recently emphasized to help teachers implement high quality curricula in the schools ( Hernández-Gantes & Nieri, 1997 ; Kruse et al., 1994 ; Loucks-Horsley et al., 1996 ; Newmann & Wehlage, 1995 ; Nickolas, 2000 ).

In sum, although the quality of the units varied, our findings suggested that it is possible for interdisciplinary teams of mathematics and VTE teachers to create high quality integrated curriculum units if certain conditions are met. Team dynamics, teachers' beliefs, and school supports, in particular, appeared to be critical to sustain productive collaborative curriculum development work. It appeared that having support from the school's community, meeting regularly with all the team members, focusing conversations toward student understanding and writing tasks that promote conceptual and integrated understanding of the concepts, and writing the unit together with reflective thought, all seemed to be critical complementary conditions in successful integrated unit writing.

Implications

An array of policy recommendations are presently calling for, among other changes, increased attention to authentic and integrated learning, work-based learning and community service, professional collaboration among teachers, and the use of alternative assessments to build systems for continuous learning and school improvement ( Grubb, 1997 ; National Council of Teachers of Mathematics, 2000 ; Mathematical Sciences Education Board, 1995 ). While implementing these new modes of educating is widely advocated, there are only a limited number of systemic efforts underway to assist educators in developing locally responsive approaches to these challenges. Furthermore, the research base for conducting interdisciplinary curriculum integration initiatives in secondary schools and post-secondary institutions is largely undeveloped. In this context, the findings of this study are both humbling and promising. Results are humbling because they show the difficulties in breaking down traditional beliefs of curriculum and instruction for the development of highly dynamic collaborations. Concurrently, in spite of the many interdisciplinary barriers which slow down the development of shared understandings about integration and authenticity, our analysis also suggests promising prospects for developing integrated, standards-based curricula. When given appropriate programmatic support, adequate time, and conceptual guidance, mathematics and vocational education instructors can develop effective collaborative efforts to write curriculum materials that integrate mathematical and career concepts, are based upon common principles which underlie both mathematics and VTE reform, and represent high quality authentic student work.

It is important to realize that if we are to have an impact on both teaching constituencies, professional development programs have to include topics that are relevant to integrated curriculum development collaboration, allow teachers to provide input on program design, and provide funding opportunities for continued collaboration. Schools should promote holistic understandings of common reform principles and encourage teachers to agree upon criteria for high student achievement, integrated curricula, instructional practices, and assessment strategies. Research on the impact of school culture and leadership on interdisciplinary teacher collaboration and, in turn, the impact of integrated curricula on students' mathematics learning and career development must be conducted. This line of research is particularly important to determine whether some forms of supports and integration are more effective than others and to measure the effects on mathematics learning and students' career development.

References

Adajian, L.B. (1995) . Teachers' professional community and the teaching of mathematics (collaboration) . Unpublished doctoral dissertation, University of Wisconsin-Madison.

American Mathematical Association of Two-Year Colleges. (1995) . Crossroads in mathematics: Standards for introductory college mathematics before calculus . Memphis, TN: Author.

Betances, C. A. (1999) . From professional development to practices: Factors in the implementation of standards-based curriculum and instruction . Unpublished doctoral dissertation, George Washington University.

Bottoms, G., & Sharpe, D. (1996) . Teaching for understanding through integration of academic and technical education . Atlanta, GA: Southern Regional Education Board.

Brendefur, J. (1996) . Creating and revising authentic curriculum units. MathNet News , l(l), 5,7.

Brendefur, J., Hernández-Gantes, V., & Webb, N. (Fall 1998). MathNet Evaluation Report . Center for Education and Work: University of Wisconsin-Madison.

Brown, J. S., Collins, A., & Duguid, P. (1989) . Situated cognition and the culture of learning. Educational Researcher , 18(l), 32-42.

Dougherty, B., & Ellibee, M. (1996) . Curriculum quality standards for school-towork: A guidebook . Berkeley, CA: National Center for Research in Vocational Education.

Glaser, B.G. & Strauss, A.L. (1967) . The discovery of grounded theory: Strategies for qualitative research. Chicago: Aladine Publishers, CO.

Gray, K. C., & Herr, E. L. (1995) . Other ways to win: Creating alternatives for high school graduates . Thousand Oaks, CA: Crown Press.

Grubb, W.N. (1997) . Not there yet: Prospects and problems for "education through occupations." Journal of Vocational Education Research , 22(2), 77-94.

Grubb, W.N. (Ed.). (1995) . Education through occupations in American high schools. Volume I: Approaches to integrating academic and vocational education . New York, NY: Teachers College Press.

Hernández-Gantes, V. M., & Nieri, L. A. (1997) . Linking the NCTM standards to emerging vocationalism . Berkeley, CA: National Center for Research in Vocational Education.

Kruse, S., Seashore, L. K., & Bryk A. (1994) . Building professional community in schools. Issues in Restructuring Schools, Report No. 6 , pp. 3-6. Madison, WI: Center on Organization and Restructuring of Schools.

Locke, M. S. (1999) . Teacher attitudes toward implementation of school-based learning components, work-based learning components, and connecting activities, and use of instructional strategies related to school-based learning . Unpublished doctoral dissertation, University of La Verne.

Loucks-Horsley, S., Stiles, K., & Hewson, P. (May, 1996) . Principles of effective professional development for mathematics and science education: A synthesis of standards. NISE Brief , 1(1), pp. 1-6.

Mathematical Sciences Education Board. (1995) . Mathematical preparation of the technical workforce: Report of a workshop . Washington, DC: National Research Council.

Merriam, S.B. (1998) . Qualitative research and case study applications in education . San Francisco: Jossey-Bass.

National Center for Education Statistics. (1996) . Pursuing excellence. A study of U.S. eighth-grade mathematics and science teaching, learning, curriculum, and achievement in international context (NCES 97-198 ). Washington, DC: U.S. Government Printing Office.

National Council of Teachers of Mathematics. (1989) . Curriculum and evaluation standards for school mathematics . Reston, VA: Author.

National Council of Teachers of Mathematics. (1991) . Professional standards for the teaching of mathematics . Reston, VA: Author.

National Council of Teachers of Mathematics. (1995) . Assessment standards for school mathematics . Reston, VA: Author.

National Council of Teachers of Mathematics. (2000) . Principles and standards for school mathematics . Reston, VA: Author.

Newmann, F. M., & Associates. (1996) . Authentic achievement: Restructuring schools for intellectual quality . San Francisco, CA: Jossey-Bass.

Newmann, F. M., & Wehlage, G. G. (1995) . Successful school restructuring: A report to the public and educators . Madison, WI: Center on Organization and Restructuring of Schools, University of Wisconsin.

Newmann, F. M., Secada, W. G., & Wehlage, G. G. (1996) . A guide to authentic instruction and assessment: Vision, standards and scoring . Madison, WI: Wisconsin Center for Education Research.

Nickolas, M. (2000) . Teacher collaboration: A survey of factors, attitudes, and preferences affecting implementation in mathematics . Unpublished doctoral dissertation, University of Pennsylvania.

Peterson, P. L., McCarthey, S. J., & Elmore, R. F. (1996) . Learning from school restructuring. American Educational Research Journal , 33(l), 119-153.

Phelps, L. A. (1992) . Designing effective education-work linkages. Issues in Education and Work . Madison, WI: University of Wisconsin, Center on Education and Work.

Phelps, L. A., Hernández-Gantes, V. M., Jones, J., Sanchez, D., & Nieri, A. H. (1995) . Students' indicators of quality in emerging school-to-work programs. Journal of Vocational Education Research , 20(2), 75-102.

Porter, A. C., Kirst, M. W., Osthoff, E., Smithson, J. L., & Schneider, S. A. (1994) . Reform of high school mathematics and science and opportunity to learn . New Brunswick, NJ: Rutgers University, Consortium for Policy Research in Education.

Romberg, T. A., & Carpenter, T. C. (1986) . Research on teaching and learning of mathematics: Two disciplines of scientific inquiry. In M. C. Wittrock (Ed.), Handbook of research on teaching (3rd ed., pp. 850-873). New York: Macmillan Publishers.

Schmidt, B. J., Finch, C. R., Faulkner, S. L., & Kandies, J. (1995) . Preparing teachers to successfully integrate vocational and academic education: A case study approach . Berkeley, CA: National Center for Research in Vocational Education.

Secada, W., & Byrd, L. (1993) . Classroom observation scales: School level reform in teaching of mathematics . Madison, WI: National Center for Research in Mathematical Sciences Education, University of Wisconsin-Madison.

Spillane, J. P., & Zeuli, J. S. (1999) . Reform and teaching: Exploring patterns of practice in the context of national and states mathematics reform. Educational Evaluation and Policy Analysis , 21(1), 1-27.

Spradley, J. (1979) . The ethnographic interview . New York: Holt, Rinehart, & Winston.

Stake, R.E. (1994) . Case studies. In N. K. Denzin, & Y. S. Lincoln (Eds.), Handbook of qualitative research , 236-247. Thousand Oaks, CA: Sage Publications.

Stasz, C., Kaganoff, T., & Eden, R. (1994) . Integrating academic and vocational education: A review of the literature, 1987-1992. Journal of Vocational Education Research , 19(2), 25-72.

Stigler, J., & Hiebert, J. (1999) . The teaching gap . New York, NY: Freedom Press.

Strauss, A.L. (1987) . Qualitative analysis for social scientists . Cambridge: Cambridge University Press.

United State Congress. (1994) . School to Work Opportunities Act of 1994 (P.L. No. 103-239). Washington, DC: Author.

Wirth, A. G. (1992) . Education and work for the year 2000: Choices we face . San Francisco: Jossey-Bass.

Wolcott, H.F. (1994) . Transforming qualitative data: Description, analysis, and interpretation . Thousand Oaks, CA: Sage.

Appendix

Urban High Schools

Kentucky School . An urban high school where minorities are bused from inner city projects. The school has an enrollment of 1,200 students and is a Magnet Career Academy for Public Safety Careers. The school has a record of support for teacher collaborative practices.

Minnesota School . An urban high school located in a federally-designated enterprise community serving 1,150 students from diverse backgrounds. The teacher-team enjoyed district support but was working together for the first time.

Wisconsin School . This urban high school has an enrollment of about 1,600 students. Teachers had been working on the integration of mathematics and VTE for several years but had no sustained collaborative efforts.

Suburban High Schools

New Jersey School . A suburban high school located 12 miles west of New York and serving about 775 students. The teacher-team had been working together for several years in a sustained effort to integrate mathematics and technology in a variety of grade and ability levels.

California School . The high school is located in Southern California and serves about 1,876 students a year. Several teams of teachers team-teach in various areas but had no sustained collaborative efforts in the integration of mathematics and VTE.

Rural High Schools

Michigan School . This Vocational Center serves 15 school districts from three counties and has an annual enrollment of 867 students. The center offers a Manufacturing Academy in cooperation with a local community college. The teacher-team enjoyed school support but was working together for the first time.

South Carolina School . This is a rural high school serving 576 students a year. The school is 21 miles away from the nearest metropolitan area. The school has a record of support for collaborative efforts and is one of 18 Advanced Integration Model Sites with the Southern Regional Education Board.

Post-Secondary

Texas Community College . The college serves about 20,000 full-time/part-time students. Teachers had been formally working on integration efforts for several years under Perkins Grant initiatives. The teacher-team enjoyed college support but was working together for the first time and team members were located in different campuses.

The Authors

Victor M. Hernandez is Senior Educational Researcher in the Center for Educational Technologies at Wheeling Jesuit University, 316 Washington Avenue, Wheeling, West Virginia 26003. [E-mail: vmgantes@cet.edu ]. His research interests are contextual teaching and learning, professional development, and impact of career-oriented programs on student learning and career development.

Jonathan L. Brendefur is Assistant Professor of curriculum and instruction at Boise State University, 1910 University Drive, Boise, Idaho 83725. [E-mail: jbrendef@boisestate.edu ]. His research interests are mathematics education, curriculum development, students' thinking, and professional development.