JITE v36n2 - Comparison of Applied Mathematics Skill Levels for Students Enrolled in Applied Versus Traditional Courses at Secondary Schools
Comparison of Applied Mathematics Skill Levels for Students Enrolled in Applied Versus Traditional Courses at Secondary Schools
Dennis Wayne Field
Iowa State UniversityIntroduction
A report released by the American College Testing's (ACT) Center for Education and Work ( 1995 ) relays the frustration of employers who believe that school curricula are not sufficiently focused on preparing students for work; particularly in the areas of mathematics, communications, and teamwork. Employers in Iowa and elsewhere perceive a gap between the existing skill levels of students leaving high school and the skill levels described as needed in the 1991 Secretary's Commission on Achieving Necessary Skills report for effective job performance in today's high performance workplace. Mindful of this, in 1993 a non-profit, politically independent group, the Iowa Business Council (IBC), composed of the leadership from approximately 20 major employers in Iowa initiated a project to accomplish two objectives to:
- improve communications with educators, and
- quantitatively articulate both the nature and levels of skills needed by high school graduates to qualify for certain entry-level positions in its member companies.
The Iowa Business Council enlisted the help of the members of ACT's Center for Education and Work for this project. ACT developed a system, Work KeysÒ, to quantitatively measure certain aspects of employability skills that, under the IBC definition, include the ability to apply mathematical reasoning to work-related problems (Harriet Howell Custer, personal communication, August 31, 1995). The Work Keys system includes job profiling and work-related assessments as components. This system allows for a criterion-referenced assessment of the proficiency level of skills that are required for effective performance of a particular job in a particular company ( ACT, 1997 ).
Educators, attempting to be more responsive to the needs of students, parents, and employers, have also been involved in developing new initiatives. Various vocational programs, such as School-to-Work and Tech Prep, have been established at both state and federal levels in an attempt to close the aforementioned gap between education and employability skills. The applied academics component of Tech Prep is one such effort ( Hershey, Silverberg, & Owens, 1995 ). In reaction to the need to strengthen skills of students coming out of high schools, Iowa schools are implementing curricular changes and many of them are implementing applied academics in the high schools. For example, of the 362 high schools surveyed during the course of this investigation, roughly 71% of them offered at least one applied academics course during the 95-96 school year ( Dugger, Lenning, Field, & Wright, 1996 ). Unfortunately, such programs are often missing essential elements needed to measure how effective the programs are in preparing students for the workforce. To date, there have been a few investigations comparing students enrolled in applied courses and traditional courses; however, this appears to be an area where more research is needed. Previous studies focusing in the area of mathematics competency include those by CORD ( 1994 ), Wang and Owens ( 1995 ), Tanner and Chism ( 1996 ), and Keif and Stewart ( 1997 ).
The CORD ( 1994 ) study compared differences in scores on an algebra exit exam between students who had completed Applied Mathematics I and II versus students who had completed Algebra I. Any students in the Applied Math group with previous Algebra I experience were excluded from the achievement measures as a control for prior learning experience, but no other concomitant variables appeared to be controlled in this study. The exit exam used was the product of a joint development effort by CORD staff and mathematics consultants and was designed to assess algebra skills. CORD reported no significant differences (at an alpha level of .05) in these mean test scores. The sample selection for the study was non-random.
The 1995 paper by Wang and Owens summarized the results of an applied academics project sponsored by the Boeing Company. In the abstract of this paper Wang and Owens reported that Applied Mathematics students scored significantly higher than their peers in traditional mathematics classes on an applied mathematics test developed by the Northwest Regional Educational Laboratory (NWREL). Wang and Owens ( 1995, p. 16 ) further reported that when controlling for gender, grade level, overall grade in mathematics, and overall grade point average, applied math students still scored significantly higher than comparison students.
The Tanner and Chism ( 1996 ) investigation used the mathematics section score of a retired Scholastic Aptitude Test (SAT-M) as the dependent variable and compared the test results of students completing Applied Mathematics 2 courses and students completing their first year of Algebra 1. They stated that students in the sample were from all socio-economic levels and attempted to adjust for some student differences by using students' eighth grade Iowa Test of Basic Skills mathematics total score as a covariate. Tanner and Chism reported that students completing the Applied Mathematics 2 classes scored significantly higher ( p = .00) on the SAT-M than did students completing the Algebra 1 classes.
Keif and Stewart's ( 1996 ) data indicated that there was no significant difference ( p = .79 given F [4, 249] = 0.43) among mean scores on the Work Keys Applied Mathematics test for students completing Applied Mathematics 1, Applied Mathematics 2, and Algebra 1 after adjusting for 8 th grade Missouri Mastery Achievement Test (MMAT) scores in math and reading. They reported that the General Linear Models analysis of covariance procedure was used to compare the groups while statistically controlling for the difference in entry skills indicated by the MMAT. Keif and Stewart, noting that the first and second year students in applied math did not score significantly different on the Work Keys Applied Mathematics test, offered an explanation that perhaps the test is designed to assess job entry behavior and primarily addresses only those skills covered in the first 15 units of the CORD Applied Mathematics program.
Definition of Terms
- Applied academics courses ( Hull, 1995 ) are those developed by the Center for Occupational Development (CORD) or the Agency for Instructional Technology (AIT). The courses are entitled Principles of Technology, Applied Biology/Chemistry, Applied Mathematics, and Applied Communications. The curricula are written at an 8th grade reading level, incorporate contextual examples, and are targeted to the middle 50% of high school students.
- Guttman-based Tests are tests that are based on a scaling procedure by which responses to items would place examinees in perfect order. This means that an examinee of higher rank can correctly answer all the items that are correctly answered by an examinee of lower rank, plus at least one more item. Examinees are ordered by ability (number of items answered correctly), and items are ordered by difficulty (number of examinees who answered incorrectly) ( ACT, 1997, p. 19 ).
- Homoscedasticity is the term used to report a condition of equal error variances
- Iowa Test of Educational Development (ITED) is a standardized test designed to assess current performance in reading, language, and mathematics. Individual achievement is determined by comparison of results with average scores derived from large representative samples and is communicated as a percentile rank score. For purposes of this investigation, the Iowa percentile rank of the students taking the test was used. The Iowa percentile rank of an individual's score indicates the portion of the group of students in Iowa at a comparable grade level who scored below the level assigned to that student on the test. For example, with a score at the 50th percentile, half of the group scored lower; a score at the 80th percentile indicates that 80 percent scored lower than the student.
- Work Keys Tests are a series of Guttman-based tests designed to assess personal skill levels in important areas of employability skills ( ACT, 1997 ). There are currently eight tests: (a) Applied Mathematics, (b) Applied Technology, (c) Listening, (d) Locating Information, (e) Observation, (f) Reading for Information, (g) Teamwork, and (h) Writing.
Purpose of the Study
This study was designed to answer the question: "Are students' abilities to apply mathematical reasoning to work-related problems (as indicated by their Work Keys Applied Mathematics test results) different for students who are enrolled in applied academics courses as compared to students who are enrolled in equivalent traditional courses?"
The reader should note that the design of this investigation was NOT one that would allow a claim that observed differences could be attributed to the superiority of one instructional method over the other. This study was designed to provide quantifiable baseline results regarding differences between two groups of high school students.
Method
This study involved the use of intact classes, and while the use of preexisting groups is not without its problems (see Pedhazur, 1982 ), this lack of true randomization is not a major issue if one is simply characterizing the differences between the groups (as was the case here) and not attempting to use the results as validation of a certain instructional method.
Once the decision to use intact classes had been made, choices regarding the unit of analysis and analytical method for the two groups of students (that is, those enrolled in applied versus traditional classes) moved to the forefront. In choosing the method of analysis, the assumptions underlying the technique had to be taken into account. Student's t-test, for example, relies on two critical assumptions: (1) that the observations have a common normal distribution with mean m and variance s 2 ; and (2) that the observations are independent ( MathSoft, 1997, p. 48 ). Traditional linear model analysis assumes linearity, normality, homoscedasticity, and independence ( Bryk & Raudenbush, 1992, p. xiv ). Whether data are normally distributed is easily checked and nonparametric methods exist to accommodate data that do not meet the standard assumption of normality. One cannot in good conscience, however, make the assumption of independence at the individual student level since groups of students are aggregated in classes and to perform the analyses solely on aggregated class level data is to ignore the wealth of within-class variation. In addition, even at the class level, the assumption of independence of classes within the same school could be questioned. These unit-of-analysis questions have been the focus of a number of researchers over the past 25 years (for example, Bryk & Raudenbush, 1992 ; Cronbach, 1976 ; Cronbach & Webb, 1975 ; Iversen, 1991 ; Pedhazur, 1982 ) and multilevel models are increasingly being used to address unit-of-analysis concerns. In Bryk and Raudenbush ( 1992 ), the series editor, Jan de Leeuw concludes that while multilevel models are not the solution to all data analysis problems of the social sciences, technically they are a big step ahead of aggregation and disaggregation methods, because "they are statistically correct and do not waste information" ( p. xv ). Using a multilevel model, one is able to relax two of the four basic assumptions of the traditional linear model, homoscedasticity and independence. A multilevel model based on the Hierarchical Linear Models (HLM) approach discussed by Bryk and Raudenbush ( 1992 ) was used in this investigation. The data were analyzed using off-the-shelf HLMä software ( Bryk, Raudenbush, & Congdon, 1996 ).
Participants
The sample for the study was drawn from a population consisting of high school students, grades 9 through 12, enrolled in one of eight Iowa public high schools during the 1995-1996 school year. The high schools chosen for the study were selected from an original list of approximately 60 schools. This list was compiled based on the recommendations of individuals knowledgeable about applied academics efforts in the state. After looking at a number of school characteristics, class size; willingness of teachers, administrators, and students to participate in the study; and whether the instructional methods were 100% applied/traditional or some amalgamation of the two, eight schools were chosen to participate in the study. The sample for the study includes 790 students, split relatively evenly between applied and traditional courses, although not all requested data were available for all students. When all data sets with missing data were eliminated, information on 591 students remained. It should be noted, however, that if the missing data were not relevant to the analysis performed, the remaining pertinent data in that data set were used in the analysis.
Instrument
The Work Keys Applied Mathematics test score served as the measure of a student's skill level in applied mathematics. The operational form of the test used is described, briefly, below ( ACT, 1997, p. 67 ):
The Applied Mathematics assessment measures the examinee's skill in applying mathematical reasoning to work-related problems. The test questions require the examinee to set up and solve the types of problems and do the types of calculations that actually occur in the workplace. This test is designed to be taken with a calculator. As on the job, the calculator serves as a tool for problem solving. A formula sheet that includes all formulas required for the assessment is provided.
This assessment contains questions at five levels of complexity, with Level 3 being the least complex and Level 7 being the most complex. The levels build on each other, each incorporating the skills assessed at the preceding levels. Examinees are given 40 minutes to solve 30 multiple-choice questions.
Estimates of reliability parameters for the Applied Mathematics assessment test are included in ACT's Preliminary Technical Handbook ( ACT, 1997 ). Table 3.3 in the Handbook ( ACT, 1997, p. 23 ) reports two different raw score reliability coefficients for the Applied Mathematics assessment test, the first being the KR 20 and the second being a reliability coefficient calculated using a probabilistic item-response theory (IRT) approach. The KR 20 s for three forms of the Applied Mathematics test ranged from .80 to .83, while the IRT approach for the tests yielded reliability coefficients that ranged from .82 to .85. The coefficient of reproducibility ( Stouffer, et al., 1950, p. 117 ) was reported as .975 for the Applied Mathematics assessment test ( ACT, 1997, p. 20 ).
The topic of Work Keys assessment test validity was less open to summary presentation by various validity coefficients than the issue of reliability. In 1971, Cronbach (as cited in Crocker & Algina, 1986 ) described validation as a process whereby evidence is collected to support the types of inferences that are to be drawn from test scores. Crocker and Algina ( 1986 ) go on to state that in planning a validation study, the desired inferences must be clearly identified. Validation, in the case of the Work Keys assessment tests, was not a simple matter since, according to ACT ( 1997 ), Work Keys scores are used in a variety of ways, necessarily resulting in validity studies which encompass a wide variety of approaches and types of evidence. However, with respect to content validation, ACT used panels of qualified content domain experts in the test development process. The development process included input by advisory panels composed of business people and educators knowledgeable in the topic areas and examination by both content and fairness reviewers. The development effort also included the process of matching items to the performance domain through a comparison of job skill requirements versus Work Keys skill scales by subject matter experts. The subject matter experts, usually individuals who were doing or had recently done the job profiled, were asked to classify job skill requirements relative to the Work Keys skill scale. The conclusion of the ACT staff after reviewing the results from 1,100 profiled jobs was that the results "strongly suggest" that the Work Keys skill scales are content valid for large numbers of jobs ( ACT, 1997, p.52 ).
Additional information is supplied in the Preliminary Technical Handbook ( ACT, 1997 ) and the interested reader is referred to that document for a more complete description of the process followed by ACT to ensure validity of their assessment tests.
Procedure
Once schools were selected, the project team worked with each school to identify and schedule equivalent classes to take the Work Keys assessment tests. Table 1 matches applied academics courses with traditional courses at the chosen schools.
The following data for all students in the target classes were collected during the 1995-1996 school year: (a) high school; (b) course type, applied or traditional; (c) course, math, English, physics, etc.; (d) class; (e) student; (f) grade level, 9 through 12; (g) student cumulative high school grade point average (GPA), 0 to 4.00; (h) percentile rank of the student's Iowa Test of Educational Development (ITED) composite score , 0 to 100; and
Table 1 Course Equivalency
Applied Course Traditional Course
Applied Math I Algebra I Applied Math II Algebra II, Trigonometry, or Geometry Applied Communications Traditional English Principles of Technology I Physics Applied Biology/Chemistry Traditional Biology/Chemistry
(i) Work Keys test score. The tests were administered near the
end of the 1995-1996 school year.As a first step in the data analysis, a descriptive analysis of the raw data was completed. This included gender, grade level, grade point average, ITED and Work Keys score distributions. Following the descriptive analysis, exploratory data analysis (EDA) was conducted to determine if the data met certain statistical assumptions regarding the shapes of their distributions, to detect the presence of outliers, and to do a gross check on the bivariate relationship of variables involved in the study. The EDA consisted of generating and evaluating a number of standard plots of the data, including histograms, boxplots, density plots, normal probability plots, and scatterplots, along with correlation matrices.
The research question was then addressed using hierarchical linear models as described by Bryk and Raudenbush ( 1992 ). Analyses using hierarchical models requires one to choose among options in three areas: the number of levels in the analysis; the choice of parameters to be included in the model; and finally, the choice between fixed, random, and nonrandomly varying parameters.
There are a tremendous number of alternative modeling possibilities with HLM. For example, a two-level model might take the form of repeated observations of student performance over the course of an academic year. Here the repeated observations (Level 1) data are nested within each student (Level 2). Other possible two-level models would be students (Level 1) within classes (Level 2); or students (Level 1) within teachers (Level 2). One could increase from a two-level to a three-level model by adding classes as the third level, for example repeated observations within students within classes or schools students within classes, within schools, as was done in this investigation. The choice of number of levels is somewhat data driven, one initially looks at a fully unconditional model. That is, one does not attempt to explain variance, but simply partition it among levels and make the decision as to whether the amount of variation at a specific level is enough to warrant including that level in the model. If, for example, 66% of the variance is observed at Level 1, 33% of the variance is associated with Level 2, and only 1% is observed at Level 3, a less complex two-level model would seem to make more sense. In such a situation, the Level 3 variance would simply become part of the Level 2 error term and a two-level, fully unconditional model would report 66% of the variance at Level 1 and 34% of the variance at Level 2.
The choice of parameters to include at each level in the model and the choice between fixed, random, and nonrandom varying parameters follows the same logic. One may include various parameters in the model, specifying them as fixed, random, or nonrandom varying, and observe whether each parameter explains a significant amount of variation at that level. The results can be reported as a variance reduction by level from the fully unconditional model. The choice of how to model the Level-1 and Level-2 regression coefficients, fixed, random, or nonrandom varying, is essentially data driven. Other theoretical and empirical considerations also come into play, however it is beyond the scope of this paper to cover all aspects of building and assessing hierarchical models, and the interested reader should consult the text by Bryk and Raudenbush (1992) for more complete coverage.
The initial three-level (students within classes within schools) hierarchical model used in this investigation is described below. The mathematical representation of this model is provided in Appendix A .
Level-1: Within each classroom, students' abilities to apply mathematical reasoning to work-related problems (Work Keys Applied Mathematics assessment test scores) are modeled as a function of a number of student-level predictors; including ITED score, GPA, gender, and grade level, plus a random student-level error.
Level-2: Each Level-1 coefficient is modeled by classroom-level characteristics such as curricula type (applied or traditional) and relevant topic (math or non-math) for a specific class.
Level-3: Each Level-2 coefficient is modeled by an assessment test score grand mean plus a random school-level error term.
Results
The original sample of 790 students resulted in complete data for 591 students after eliminating series with missing or obviously erroneous data points. Tables 2 and 3 provide the gender and grade level splits, respectively, for the applied and traditional student groups.
One other initial area of interest related to student, or Level 1, demographics was the split between students above and below the minimum skill level cutoff score of 3 on the Work Keys Applied Mathematics test. Table 4 presents a detailed summary of student results for this test.
Table 2 Gender
Female Male Totals
Applied 105 160 265 Traditional 190 136 326 Totals 295 296 591
Table 3 Grade in School
Grade Applied Traditional Totals
9 78 127 205 10 90 97 187 11 30 21 51 12 67 81 148
Totals 265 326 591
Table 4 Course Enrollment of Students Scoring Above and Below Minimum Skill
Level Cutoff on Work Keys Test
Applied Mathematics Frequency of Test Scores Student
Totals<3 as %
of Totals<3 >=3
Applied Math I 6 129 135 4% Algebra I 2 144 146 1% Algebra II 2 79 81 2% or Geometry 0 95 95 0% Traditional English Courses 1 71 72 1% Principles of Technology I 1 71 72 1% Physics 0 8 8 0% Applied Biology/Chemistry 4 89 93 4% Traditional Biology/Chemistry 3 80 83 4% Totals 20 770 790 3%
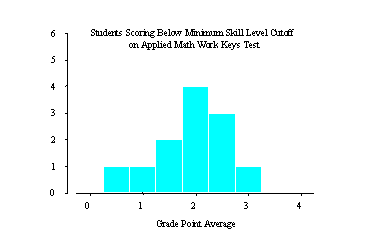
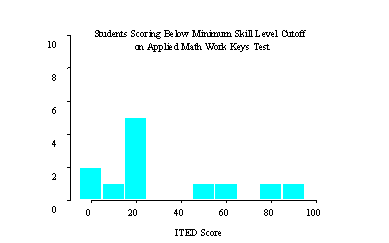
Figure 1 provides histograms of ITED score and Grade Point Average (GPA) for all students who scored below the minimum skill level score on the Applied Mathematics test and for whom GPA and ITED data were available. It is obvious from the graphs that students' scores falling below the minimum skill cutoff score of 3 were not only those with an ITED score or GPA at the low end of the scale.
During exploratory data analysis, significant correlation (r = .74 at p = .00, see Table 5 ) was observed between the ITED scores and GPA.
Figure 1 GPA and ITED histograms of students scoring below the minimum skill level of 3 on the Work Keys Applied
Mathematics test
In an attempt to avoid the problems inherent in using the highly correlated variables GPA and ITED together as independent variables in an HLM regression equation, the decision was made to combine GPA and ITED scores into a new variable called "ACHIEV". Both GPA and ITED scores were to receive equal weighting in calculating ACHIEV. In order to scale the GPA score range (0 to 4) so that it was consistent with the ITED score range (0 to 100) and weight both equally, the average of the ITED score and 25 times the GPA was used. ACHIEV has the advantage of damping the effect of a "bad day" that a student might have experienced when taking the ITED, but still allows the use of a standardized test independent of variations in grading policies. It minimizes the loss of information one would
incur by eliminating one or the other entirely from the model. The correlation coefficient for the new variable ACHIEV and the Work Keys Applied Mathematics test score was essentially the same as that listed in Table 5 for the ITED score and the Work Keys Applied Mathematics test score; that is, .59 on 579 cases.
Statistical Data Analysis
The impact of curricula type was analyzed using Hierarchical Linear Modeling (HLM). Using a fully unconditional model, one can partition the variance across levels. The result of this partitioning process is shown in Table 6 .
Table 7 provides the summary results of the Level 2 and Level 3 reliability calculations for the Work Keys test. A reliability close to .50 indicates that the parameter variance component and the error variance component are essentially equal. One would therefore interpret the Level 2 reliability shown in Table 5 to mean that it would be difficult to discriminate among classrooms within the same school simply by looking at the classroom sample mean; the estimates of the within- and between-class variances are approximately the same size. The Level 3 value is a measure of the average reliability of each school's sample mean as an estimate of its true mean.
Three predictor variables were evaluated at Level 1 of the model; ACHIEV (the composite of ITED and GPA), GENDER, and GRADE (the student's year in school). Two predictor variables were also evaluated at Level 2 of the model; TYPE (applied versus traditional course) and RELVNT (a dummy variable used to indicate whether or not the course material was relevant to the material covered in the Work Keys test--for example, math and physics courses were relevant to the Applied Math test, while communications and biology courses were not). No school level predictor variables were used; however, school-level random components were included in the Applied Math model.
Table 5 Correlation Matrix for Students Taking the Applied Mathematics Work
Keys Test and Receiving a Score Above the Minimum Skill Level of Three (3)
WK.
ScoreITED GPA Grade Gender WK.
Score1.00 .59 .50 .29 .19 (579) (579) (579) (579) (579) p = na p = .00 p = .00 p = .00 p = .00 ITED .59 1.00 .74 .06 -.07 (579) (579) (579) (579) (579) p = .00 p = na p = .00 p = .18 p = .10 GPA .50 .74 1.00 .04 -.16 (579) (579) (579) (579) (579) p = .00 p = .00 p = na p = .38 p = .00 Grade .29 .06 .04 1.00 .03 (579) (579) (579) (579) (579) p = .00 p = .18 p = .38 p = na p = .45 Gender .19 -.07 -.16 .03 1.00 (579) (579) (579) (579) (579) p = .00 p = .10 p = .00 p = .45 p = na (Coefficient / (Case) / 2-tailed Significance)
Table 6 Three-level, Fully Unconditional Model
Applied Mathematics
Variance Decomposition
by LevelStudents Classes Schools
Level 1 72% 18% 10%
Applied Mathematics HLM Analysis
As can be seen in Table 8 , over 60% of the class-level variation is explained by the Applied Mathematics model. Noting the p value of .00 for the random effect at Level 2, however, one may conclude that a significant amount of unexplained variation remains at this level. The "Curricula gap" coefficient is a positive
Table 7 Level 2 and Level 3 Reliability Calculations
for the Work Keys Applied Mathematics
Applied Mathematics
Level 2 Classes .43 Level 3 Schools .72
0.79 indicating that students enrolled in traditional courses averaged over 3/4 of a point higher on the Work Keys Applied Mathematics test than students enrolled in applied courses. Male students scored on average approximately 4/10 of a point higher than did female students. The ACHIEV coefficient is positive, which simply means those students with higher combined GPA and ITED scores also scored higher on the Work Keys test than those with lower combined GPA and ITED scores. Student grade level was also significant; with each increase in grade level being "worth" on average approximately 2/10 of a point to the Work Keys test score over the previous grade level. An initially unexpected result turned out to be the one connected with the relevant course variable; the coefficient turned out not to be significant at the 5% level. In other words, average Work Keys scores for students enrolled in math, physics, and applied technology courses were not significantly different from those achieved on average by students enrolled in English and biology/chemistry courses (after taking into account differences in other significant variables listed in Table 8 ). One might expect students enrolled in relevant courses to do better on a math test than students enrolled in non-relevant courses; however students participating in this study as a result of their enrollment in an English course, for example, could also have been concurrently or previously enrolled in mathematics courses. In retrospect, given the mathematics requirements for all high school students, this was not a particularly surprising finding.
Table 8 HLM Estimates for Applied Mathematics Data
Fixed Effect Coefficient Se t -ratio p -value Grand mean, g 000 3.87 0.19 20.91 .00 Curricula gap, g 010 0.79 0.13 6.10 .00 Gender gap, g 100 0.43 0.09 4.83 .00 Grade level, g 200 0.19 0.07 2.74 .01 Student ACHIEV, g 300 0.03 0.00 11.08 .00
Random Effect Variance
Componentdf X 2 p value
Level 1 (Students), e (ijk) 1.03 Level 2 (Classes), r (ijk) 0.12 62 109.73 .00 Level 3 (Schools), u 00(k) 0.09 7 30.66 .00
Variance Reduction (by level) from Unconditional Model
Level 1 Students: 18% Level 2 Classes: 62%
Conclusions
Summary of Findings
The original sample of 790 students resulted in complete data for 591 students after eliminating series with missing or obviously erroneous data points. Some of the more important general observations contrasting applied versus traditional students include:
- Both ITED and GPA histograms showed traditional students with higher means than applied students in comparable courses (see Figure 2 ).
- Of all students taking the Work Keys Applied Mathematics test, approximately 3% scored below the minimum competency cutoff score of 3.
- The numbers of males and females taking the Applied Math test were roughly the same.
- There are statistically significant correlations with respect to the Work Keys test and all four concomitant variables (grade, gender, GPA, and ITED score). The 2-tailed Levels of Significance were not above .00 for any of the four variables.
- Hierarchical Linear Models were used to investigate the effect of curricula type on Work Keys scores. In each of the models a dichotomous variable associated with curricula type (applied or traditional) was included. This variable was a dummy variable associated with curricula type used in classroom j in school k . Applied courses were coded as 0 and traditional courses were coded as 1. A significant positive coefficient for this variable indicated that students in traditional courses scored higher on average than did students enrolled in applied courses, after taking into account other significant concomitant variables such as grade level, gender, and previous academic performance. The coefficient for the Applied Mathematics assessment test was 0.79 with a p value = .00 level of significance.
The answer to the central question, "Are students' abilities to apply mathematical reasoning to work-related problems (as indicated by their Work Keys Applied Mathematics test results) different for students who are enrolled in applied academics courses as compared to students who are enrolled in equivalent traditional courses?" , is a clear yes. There are disparities in prior academic performance (mean GPAs and ITED scores) and Work Keys test performance between the group of students enrolled in applied academic courses and the group of students enrolled in comparable traditional academic courses.
Figure 2 Histograms comparing students' ITED and GPA scores.
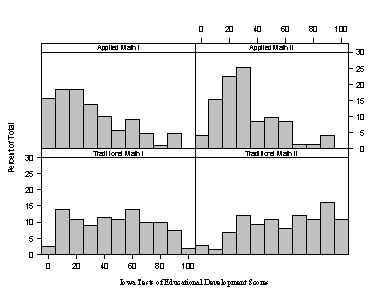
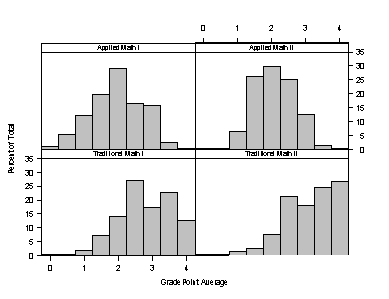
Discussion
The findings of this study do not support those obtained during the CORD ( 1994 ), Wang and Owens ( 1995 ), Tanner and Chism ( 1996 ), and Keif and Stewart ( 1996 ) studies. Their results lead to the conclusion that applied mathematics students performed equally as well, if not better, on performance tests than their comparison student groups. The data from this investigation indicated that applied students did not perform as well as traditional students on the Work Keys Applied Mathematics test. There were, however, considerable differences in the designs of the studies and the methods of analysis. Of the four other studies, only Keif and Stewart used Work Keys Applied Mathematics test scores for comparative purposes and none appeared to use multilevel models in their analyses. Covariates also differed from study to study, making direct comparisons between studies difficult. Finally, other researchers chose to compare students who had completed both Applied Mathematics 1 and 2 with students who had completed Algebra 1, even though a significant number of the Applied Mathematics 2 units relate to topics other than Algebra, such as probability, statistics, trigonometry, and geometry (see CORD, 1994, p. 5 ).
The apparent use of only student level results in the other studies could also explain differences in the results and conclusions. As an interesting exercise, the data for students enrolled in Applied Mathematics II and Algebra I from this investigation were pulled out and analyzed in a manner similar to other studies. The data included scores from 121 Algebra I students and 71 Applied Mathematics II students. In the first step, the residuals from the regression of Work Keys scores on ITED scores were obtained; this essentially adjusted the Work Keys scores for differences in students' ITED scores. These residuals were then grouped by course, Applied Mathematics II versus Algebra I, and compared using a standard two-sample t -test at the student level, ignoring the assumption of independence requirement for purposes of illustration. The results (t = 1.00, df = 190, p-value = .32) would be taken to indicate that there is no statistically significant difference between the means of the two distributions. Even if no adjustment were made for the ITED scores of students, the results (t = -1.51, df = 190, p-value = .13) would still indicate that there is no statistically significant difference between the means of the two distributions. Although use of the t -test is not endorsed by the author for these data, the assumption of independence for students nested within classes is not justified, such an analysis does offer the reader the opportunity to contrast methodologies and results from this and previous studies.
Noting that the results of this study indicated that applied students did not perform as well as traditional students on the Work Keys Applied Mathematics test, some may find it tempting to conclude that traditional teaching methods are superior to applied academics. Such a conclusion is unwarranted given the use of intact groups and the significant amount of unexplained variation at both the student and class levels. Student performance was not being compared under true experimental conditions; nor can one discount the possibility of omitted intercorrelated independent variables in the HLM regression equations. Failure to control certain variables may result in attributing differences in mathematics skills to instructional method, when in fact one or more of the covariates are correlated with variables not included in the equation but which are nevertheless related to the dependent variable.
Given the findings of this investigation, one would argue that the effectiveness of the applied mathematics curricula could not be determined solely from simple test scores. Although traditional students did better on average on the Work Keys tests than did applied students in this study, test scores are not the only indicators of employability skills. Proponents of applied academics have suggested additional measures of effectiveness. Hull ( 1995, p. 70 ), for example, lists the following criteria:
- Students are able to transfer knowledge from academic content to vocational applications and from school to the workplace.
- Students are not afraid to take subjects such as mathematics and science.
- Students display more interest, motivation, and understanding of the value of the subject and of school in general than they did in traditional classes.
- Students that have traditionally done poorly in academic subjects display improved performance.
- Applied courses are as challenging as the traditional courses in the same subject.
There is certainly nothing in this investigation to indicate that applied mathematics courses are not effective when measured against objectives such as those attributed to Hull. Indeed, based on lessons learned during this investigation, one may conclude that to fully study the effectiveness of applied mathematics researchers must:
Broaden the investigation to include additional measures of effectiveness, such as those suggested by Hull ( 1995 ).
- Monitor growth of students' mathematics skills over time. Data should be collected at periodic intervals for analysis and should include measures of performance in both school and workplace. Data collected and analyzed during this investigation are the start of a reasonable set of baseline numbers, but repeated observations are needed. Applied academics curricula are relatively new additions to many school systems and a "learning curve" exists with respect to their implementation. Tracking changes over time is of particular importance if the measures of effectiveness suggested by Hull are to be examined. Care must also be taken in the choice of when data are to be collected. One data collection site reported that students, particularly seniors, were less apt to put forth their best efforts when tests were administered near the end of the school year.
- Investigate other independent variables that may account for the significant unexplained variability related to Work Keys test scores. Additional variables such as socioeconomic status, teacher-to-pupil ratio, training in applied teaching methods, and pattern and frequency of previous mathematics instruction may be important.
- Verify content of applied and traditional courses to ensure that they are indeed comparable. This study matched Applied Mathematics I with Algebra I, while others matched Applied Mathematics II with Algebra I.
- Examine the foundation assumptions inherent to the choice of statistical methods to be used for analyses. This investigation has attempted to point out some of the issues and pitfalls associated with the selection and use of specific statistical models.
There is favorable anecdotal evidence of the impact of applied academics curricula; the challenge continues to be how best to quantitatively assess the impact of applied academics courses. Hopefully, this study has helped to shed some further light on that important topic.
Author
Field is an Assistant Professor in Industrial Education and Technology Department, Iowa State University.
Acknowledgments
This investigation was a component of a larger study supported in part by the Iowa Department of Education. Dr. Jan Sweeney, Dr. Mandi Lively, and Mari Kemis of the Research Institute for Studies in Education at Iowa State University were involved in the initial aspects of the project. Team members, besides the author, who were actively involved throughout the project included Dr. John Dugger, Dr. Oscar Lenning, and Ms. Andrea Wright. A portion of the data collected during the project formed the basis for the author's doctoral dissertation and this manuscript. Dr. Fred Lorenz also deserves recognition for his counsel during the time statistical techniques were being investigated. The efforts of all are gratefully acknowledged.
References
ACT Center for Education and Work. (1995). Making the grade: Keys to success on the job in the 90's [Brochure]. Iowa City: Author.
ACT. (1997). Work Keys preliminary technical handbook . Iowa City: Author.
Bryk, A. S., & Raudenbush, S. W. (1992). Hierarchical linear models: Applications and data analysis methods . Newbury Park, CA: Sage.
Bryk, A. S., Raudenbush, S. W., & Congdon, Jr., R. T. (1996). HLM for windows (Version 4.01) [Computer software]. Chicago: Scientific Software International.
CORD. (1994). A report on the attainment of algebra I skills by completers of applied mathematics 1 and 2 . Waco, TX: Author.
Crocker, L., & Algina, J. (1986). Introduction to classical and modern test theory . Orlando: Harcourt Brace Jovanovich.
Cronbach, L. J. (1976). Research on classrooms and schools: Formulation of questions, design and analysis. Occasional paper of the Stanford Evaluation Consortium, Stanford, California.
Cronbach, L. J., & Webb, N. (1975). Between-class and within-class effects in a reported aptitude x treatment interaction: Reanalysis of a study. By G. L. Anderson, Journal of educational psychology, 67 (6), 717-724.
Dugger, J. C., Lenning, O. T., Field, D. W., & Wright, A. (1996). Report to the Iowa department of education: Statewide pilot study and development of a model for evaluating applied academics Across Iowa. Ames: Iowa State University, Department of Industrial Education and Technology.
Hershey, A., Owens, T., & Silverberg, M. (1995). The diverse forms of tech-prep: Implementation approaches in ten local consortia . (MRP Reference: 8087). Princeton, NJ: Mathematica Policy Research.
Hull, D. (1995). Who are you calling stupid? . Waco, TX: Center for Occupational Research and Development.
Iversen, G. R. (1991). Contextual analysis . Newbury Park, CA: Sage.
Keif, M. G., & Stewart, B. R. (1996). A study of instruction in applied mathematics: Student performance and perceptions. Journal of Vocational Education Research , 21 (3), 31-48.
MathSoft, Inc. (1997). S-PLUS 4 guide to statistics . Seattle: Author
Pedhazur, E. J. (1982). Multiple regression in behavioral research: explanation and prediction (2 nd ed.). New York: CBS College.
Secretary's Commission on Achieving Necessary Skills. (1991). What work requires of schools: A SCANS report for America 2000 . Washington, DC: U.S. Department of Labor.
Stouffer, S. A., Guttman, L., Suchman, E. A., Lazarsfeld, P. F., Star, S. A., & Clausen, J. A. (1950). Measurement and prediction . Princeton, NJ: Princeton University Press.
Tanner, C. K., & Chism, P. J. R. (1996). The effects of administrative policy on mathematics curricula, student achievement, and attitudes. The High School Journal , 79, 315-323.
Wang, C., & Owens, T. (1995). The Boeing company applied academics project evaluation: Year four. evaluation report . Portland, OR: The Northwest Regional Educational Laboratory. (ERIC Document Reproduction Service No. ED 381892).
APPENDIX A
The initial three-level (students within classes within schools) hierarchical model used in this investigation is described below.
Level-1: Within each classroom, students' abilities to apply mathematical reasoning to work-related problems (Work Keys Applied Mathematics assessment test scores) are modeled as a function of a number of student-level predictors; for example gender, grade level, a variable that takes both GPA and ITED scores into account (ACHIEV), and a random student-level error:
Y (ijk) = p 0(jk) + p 1(jk) a 1(ijk) + p 2(jk) a 2(ijk) + p 3(jk) a 3(ijk) + e (ijk)
Where Y (ijk) is the Work Keys test score of student i in class j and school k . p 0(jk) is the mean Work Keys score of 9 th grade females with a class average ACHIEV score in class j and school k . p 1(jk) is the predicted change to mean Work Keys score in class j and school k when the student is a male. This is a "gender-gap" coefficient. a 1(ijk) is a dummy variable associated with student gender. The coding is 0 for a female student and 1 for a male student. p 2(jk) is the predicted change to mean Work Keys score in class j a school k as a result of the student's grade level (9 th , 10 th , 11 th , or 12 th ). a 2(ijk) is a dummy variable associated with student grade level. The coding is 0 for a student in 9 th grade, 1 for a student in 10 th grade, 2 for a student in 11 th grade, and 3 for a student in 12 th grade. p 3(jk) is the predicted change to mean Work Keys score in classroom j and school k per unit change in the student's class-centered ACHIEV score. a 3(ijk) is the class-centered ACHIEV score of student i in class j and school k . e (ijk) is a Level-1 random effect that represents the deviation of student ijk 's score from the predicted score. These residual effects are assumed normally distributed with a mean of 0 and a variance of o 2 .
Level-2: Each Level-1 coefficient is modeled by some classroom-level characteristics such as curricula type (applied or traditional) and relevant topic (math or non-math) for a specific class.
p 0(jk) = b 00(k) + b 01(k) X 1(jk) + b 02(k) X 2(jk) + r 0(jk)
p 1(jk) = b 10(k)
p 2(jk) = b 20(k)
p 3(jk) = b 30(k)
Where b 00(k) is the mean Work Keys test score of 9 th grade females in applied non-math courses with a school mean ACHIEV score in school k . b 01(k) is the predicted change to overall class mean Work Keys test score of 9 th grade females in non-math courses with a school mean ACHIEV score in school k when traditional curricula are used rather than applied curricula. This is a "curricula-gap" coefficient. X 1(jk) is a variable associated with curriculum type used in classroom j in school k . The coding is 0 for an applied and 1 for a traditional course. b 02(k) is the predicted change to overall class mean Work Keys test score of 9 th grade females in applied courses with a school mean ACHIEV score in school k when the applied course is a math course rather than a non-math course. This is a "relevant course" coefficient. X 2(jk) is a dummy variable used to identify whether or not a course is "relevant" to the Work Keys test take in school k . The coding is 0 for a non-relevant course and 1 for a relevant course. r 0(jk) is a Level-2 random effect that represents the deviation of class j 's Level-1 intercept coefficient from its predicted value based on the Level-2 model. The random effects in Level 2 equations are assumed to be correlated. They are also assumed multivariate normal with a mean of 0. The variance of this effect is designated as t p b 10(k) is the mean slope, averaged across classes within school k , relating student gender to Work Keys score. When the coefficient is considered a fixed effect, as it is here with p 1(jk) assumed equal to b 10(k) , it implies that there are not statistically significant differences in the relationship between a student's gender and the Work Keys test score from class to class within a school. b20 (k) is the mean slope, averaged across classes within school k , relating student grade to Work Keys score. b 30(k) is the mean slope, averaged across classes within school k , relating student class-centered ACHIEV score to Work Keys score for school k .
Level-3: Each Level-2 coefficient is modeled by an assessment test score grand mean plus a random school-level error term.
b 00(k) = g 000 + u 00(k)
b 01(k) = g 010
b 02(k) = g 020
b 03(k) = g 030
b 10(k) = g 100
b 20(k) = g 200
b 30(k) = g 300
Where g 000 is the grand mean Work Keys test score of 9 th grade females, with class-centered student ACHIEV scores equal to 0, in applied non-math classes where the school-centered class mean ACHIEV score is also equal to 0. u 00(k) is a Level-3 random effect that represents the deviation of school k 's mean Work Keys score from the grand mean value based on the Level-3 model. The random effects in Level 3 equations are assumed to be correlated. They are also assumed multivariate normal with a mean of 0. The variance of this effect is designated as tp g 010 is the curricula gap coefficient averaged over schools. When the coefficient is considered a fixed effect, as it is here with b 10(k) assumed equal to g 010 , it implies that there are not statistically significant differences in the relationship between the curricula type and the Work Keys test score from school to school. g 020 is the mean slope, averaged over schools, relating the impact of "relevant" courses on the Work Keys test score. g 030 is the mean slope, averaged over schools, relating mean class school-centered ACHIEV score to (Work Keys) test score. g 100 is the mean slope, averaged over schools, relating gender to test score. g 200 is the mean slope, averaged over schools, relating grade to test score. g 300 is the mean slope, averaged over schools, relating student class-centered ACHIEV score to test score. The dichotomous variable used to identify whether or not a course was "relevant" to the Applied Mathematics test turned out not to be significant at the 5% level in this model and was eliminated from the final model.